Jijidawang

SSDFZ 集训纪要

可能算是日记性质的东西，主要是想也得记一下讲的东西，放闲话里的话似乎有点不道德 .

随时更新，想起什么就写点什么吧 .

目录

Dec. 9

可能是 Day 0 这样的内容 .

登上 QQ 发现 Alpha1022 还给我发消息了，还是关于我的闲话的，害怕 /fad

火车上整了半天 Blue Archive，加训了 15-puzzle，我感觉我已经完全会了！

歌：

  • Summer Bounce - Mitsukiyo .
  • Colorful Beach - Mitsukiyo .

晚上入坑了重返未来 1999，把可燃点抽了 .

Dec. 10

yny 讲了一些网络流的东西，前面比较平凡，后面有一些不平凡的地方然而很多都被速通了 .

CQOI2014 危桥

直接做，如果能走两次就连容量为 2 的边否则连容量为 \(+\infty\) 的边，跑两次最大流：

  • \(s\to a_1,b_1\)，\(a_2,b_2\to t\)；
  • \(s\to a_1,b_2\)，\(a_2,b_1\to t\) .

主要是为了防止 \(a_1\to b_2\)，\(a_2\to b_1\) 的情况 .

CEOI2008 order

最大权闭合子图题，可以先考虑没有租用的情况，然后再深入思考 . 具体建图为工作一排点机器一排点，源点向工作连流量为利润的边，机器向汇点连流量为购买价格的边，工作向需要的机器连流量为租用费用的边 .

洛谷 P4313 文理分科

多选一其实也挺难的 .

最小割，选一个就正常连，全选的贡献并列着连就限制好了 .

恋恋

因为看到那个 Fratured Angel 竟然是 IN 难度榜 rank 2 于是就忍痛花 16 MB 买了 .

Fratured Angel

晚上加训 gartic .

Dec. 11

下雪了 .

⑨

模拟赛又保龄了，以前都是切了能切的之后就睡觉了（所以一般就签个到走人了），现在可能需要修正一下，因为也签不上到了，光保龄容易被教练 D . 唉，这么整集训结束后我 rating 可能就前缀最小值了 .

interval

结果是一道反悔贪心的题目 . 左端点升序排序扫，动态维护两个堆 \(p,q\) 表示当前已经配对的位置和还没配对的位置，每次加入一个元素：

  • 如果有一个还没配对的位置可以配对，直接配上 .
  • 否则，如果已经配对的位置中存在一对区间 \((a,b)\)，当前区间是 \(c\)，满足 \(b\) 的右端点比 \(c\) 靠左，就拆散 \(a,b\)，转而和 \(c\) 合并，这样剩下一个 \(a\) 可以有更多的机会和后面的再合 .

时间复杂度 \(O(n\log n)\) .

apers

分层图最小割 .

对于每个点 \(u\) 拆点中间连容量为 \(c_u\) 的边，对每个入点连上一层的出点容量设 \(+\infty\)，原图的边正常连 . 这样一条路径在遇到雷的时候就只能上升一层，相当于每割一条边就表示放一个雷，割满 \(k\) 个上面就没点可走了就不连通了 .

时间复杂度 \(\Theta(\operatorname{maxflow}(nk,nk+m))\) .

circles

把 \(a_i\) 升序排序后依次加入，考虑动态维护每个环对应的链，由两个接口表达 . 记 \(dp_{i,j}\) 表示考虑前 \(i\) 个左部点现在 \(j\) 条链的答案，每次加一些右部点，分别讨论和前面的接口匹配后得到的新结果即可 . 注意最后需要减去二元环的贡献 .

时间复杂度 \(\Theta(n^2)\) .

感觉这个键盘不是很好用的样子，总是打不出来空格……不知道是不是我的问题（

不过终于知道最小割输出方案的正确姿势了，需要对源点在残量网络上 DFS 找连通块划分点集 .

NOI2008 志愿者招募

虽然不太想做 flows，不过也没啥题可做了 .

\[\begin{aligned} \mathop{\rm minimize}\limits_{\bm x} & \quad \bm c^{\mathsf T} \bm x \\ \text{s.t.} & \quad A\bm x \ge a, \ \bm x \ge \bm 0 \end{aligned}\]

其中 \(A\) 是表达每个志愿者每天是否工作的矩阵 .

对偶！

\[\begin{aligned} \mathop{\rm maximize}\limits_{\bm x} & \quad \bm a^{\mathsf T} \bm x \\ \text{s.t.} & \quad A^{\mathsf T}\bm x \le c, \ \bm x \ge \bm 0 \end{aligned}\]

考虑怎么用费用流求解，费用流的 LP 模型是：

\[\begin{aligned} \mathop{\rm minimize}\limits_{f} & \quad \sum_{(u, v)} f_{u, v} \times w_{u, v}\\ \text{s.t.} & \quad \forall(u, v), \ f_{u, v} \le c_{u,v} \\ & \quad \forall u, \ \sum_{v} f_{v, u} - \sum_{v} f_{u, v} = - b_u \\ & \quad \forall(u, v), \ f_{u, v} \ge 0 \end{aligned} \]

问题的关键就是把 \(A^{\mathsf T}\bm x \le c\) 转为费用流形式的限制（流量平衡，容量限制）. 首先引入一列辅助变量 \(\bm v\) 将不等式转为等式，限制可以进一步由容量限制刻画 . 注意到 \(A^{\mathsf T}\) 的形式比较特殊，对列差分后就是单点减了，这个可以由流量平衡刻画，从而问题转为费用流问题，使用常见的费用流算法解决即可 .

时间复杂度 \(\Theta(\operatorname{mcmf}(n,m))\) .

哈哈，垫底了 .

Dec. 12

小五

杂题选讲，很快掉线了 /youl

meme

中午颓东方，只到 gzz 三面 .

image

ARC132E Paw

答案的形态一定是一段前缀 <，一个不变的段，和一段后缀 > 拼起来 。

枚举哪段不变，两边问题本质相同，考虑把所有位置变为 < 的概率，可以 DP 预处理掉 .

\(\Theta(n)\) 解决 .

ARC135D Add to Square

？

原矩阵是 \(A\)，\(B\) 矩阵是黑白染色后将所有黑格取相反数后的矩阵 . 通过一些基本的观察只需要对于每个 \(k\) 让 \(\sum A_{i,k}-\sum B_{i,k}=0\)（列同理）即可 .

直接令 \(x_k,y_k\) 是那个式子的值，断言答案就是 \(\max\{\sum|x_i|,\sum|y_i|\}\)，下界显然，上界由构造得出：

  • 对于 \(x_i>0,y_j>0\)，让 \(A_{i,j}\gets A_{i,j}-\min\{x_i,y_j\}\)
  • 对于 \(x_i<0,y_j<0\)，让 \(A_{i,j}\gets A_{i,j}-\max\{x_i,y_j\}\) .
  • 对于 \(x_i>0,x_j<0\)，让 \(A_{x_i,1}\gets A_{x_i,1}-\min\{x_i,-x_j\}\) 且 \(A_{x_j,1}\gets A_{x_j,1}+\min\{x_i,-x_j\}\) .
  • 对于 \(y_i>0,y_j<0\)，让 \(A_{1,y_i}\gets A_{1,y_i}-\min\{y_i,-y_j\}\) 且 \(A_{1,y_j}\gets A_{1,y_j}+\min\{y_i,-y_j\}\) .

按理来说总共 \(O(n+m)\) 轮应该是 \(O((n+m)^3)\)，不过可以松过 .

md 怎么所有题 APJ 都做过 .

CF1603E A Perfect Problem

要我一直？吗 .

显然顺序不影响结果，下面只考虑不增序列 .

观察 1 一个序列是完美的当且仅当其每个子区间都是好的 .

min, max 固定的话让 \(\sum\) 一定肯定选区间最大 .

观察 2 一个序列是完美的当且仅当其每个前缀都是好的 .

\(a_ia_j\ge a_1a_j\ge\sum_{k=1}^ja_j\ge\sum_{k=i}a_j\) .

观察 3 \(a_k\ge k\) .

否则 \(\sum_{i=1}^ka_i\ge ka_1>a_1a_k\) 和观察 2 矛盾 .

观察 4 \(a_k=k\implies\forall i\le k\text{ s.t. }a_i=k\) .

首先 \(a_1a_k=ka_1\ge\sum_{i=1}^ka_i\)，另一个方向显然，从而 \(ka_1=\sum_{i=1}^ka_i\)，自然得证 .

观察 5 若 \(a_n=n+1\) 且存在 \(i<n\) 使得 \(a_i\ge i+1\)，则 \(a_{1\dots n}\) 是好的蕴含 \(a_{1\dots i}\) 是好的 .

\(a_1\ge\sum_{k=1}^n(a_k-a_1)\ge\sum_{k=1}^i(a_k-a_1)\)（第一个不等号处移项即得证）.

从而 \(a_ia_1\ge(i+1)a_1\ge\sum_{k=1}^ia_k\) .

总结一下完美序列的性质，首先令 \(a_n=n+1\)，因为 \(a_n=n\) 由观察 4 可以平凡地计算 . 需要满足条件：

  • 对于所有 \(i\le a_1\)，\(a_1\le a_i\le n+1\) .
  • 对于所有 \(i> a_1\)，\(i+1\le a_i\le n+1\) .
  • \(\sum_{i=1}^n(a_i-a_1)\le a_1\) .

枚举 \(a_1\)，让所有元素减 \(a_1\) 得到 \(\{b\}\)，则：

  • \(0\le b_i\le n+1-a_1\) .
  • \(\sum b\le a_1\) .
  • 对于 \(1\le i\le n-a_1\)，至少存在 \(i\) 个数不小于 \(n+2-i-a_1\) .

数这样的序列就可以 DP 了，\(dp_{i,j,k}\) 表示长度为 \(i\)、\(\sum b=j\)、当前要放 \(k\) 的方案数，枚举放了几个 \(k\) 即可转移 .

转移是调和级数的复杂度总总共是 \(O(n^3\log n)\) .

根据第三条限制可以得到至少 \(a_1\ge n-2\sqrt n\) 时才有贡献（实际上可以更紧），所以总复杂度是 \(\Theta(n^{3.5}\log n)\) 的 .

可能我比较劣，还得写 Barrett 模乘才能过 /kel

看到这个题的下一道是 October 18, 2017，害怕 .

CF1446D2 Frequency Problem (Hard Version)

懒得写了，胡一个跑路 . 可能以后会写这个或者 lxl 的 polylog .

初步观察是必须出现全局众数，否则可以扩张区间直到包含，一定不劣 .

枚举另一个众数，对出现次数根号分治：

  • \(c\le\sqrt n\)，直接按全局众数划分连续段从每个开头扫 .
  • \(c>\sqrt n\)，枚举众数是啥然后找包含区间 .

然后就根号平衡了，\(O(n\sqrt n)\) .

CF1610H Squid Game

为什么我配做这种题？？？？？？

ARC154E Reverse and Inversion

nmd，读错题了 .

\[f(p)=\sum_{i=1}^n(p^{-1}_i-i)p^{-1}_i=\sum_{i=1}^n(i-p_i)p_i \]

所以核心就是求 \(\sum i\cdot p_i\) 的期望 .

根据对称性和线性性就是要求每个 \(\mathbb E(p^{-1}_i)\)，然而注意到只要被翻到了翻哪里都是期望 \(\frac{n+1}2\)，这样就做完了 .

Dice Game .

Cirno

晚上加训 UNO 等 .

Dec. 13

数据结构专题好像没啥有意义的题啊 .

《惊现 lxl》

⑨

ZJOI2019 线段树

怎么到处都是标记合并题？

一次修改操作中，点分五类：

  • 一（白色）：未被完全修改的点 .
  • 二（深灰）：被打标记的点 .
  • 三（橙色）：未被修改的点，但是可以被 pushdown 到标记 .
  • 四（浅色）：被修改但是还没有 pushdown 下来的点 .
  • 五（黄色）：未被修改也不会收到标记的点 .

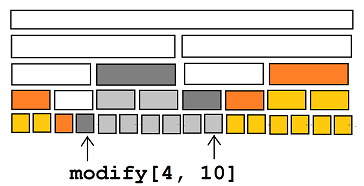
记 \(f_u\) 是有多少棵线段树里 \(u\) 号点有标记，\(g_u\) 是有多少棵树使得 \(1-u\) 都没有标记 .

那么对每次修改都可以转移 . 假设修改前有 \(k\) 棵树，则：

  • 一类：\(f'_u\gets f_u\)，\(g'_u=k+g_u\) .
  • 二类：\(f'_u\gets k+f_u\)，\(g'_u=g_u\) .
  • 三类：\(f'_u\gets k-g_u+f_u\)，\(g'_u=2\cdot g_u\) .
  • 四类：\(f'_u\gets 2\cdot f_u\)，\(g'_u=g_u\) .
  • 五类：\(f'_u\gets 2\cdot f_u\)，\(g'_u=2\cdot g_u\) .

线段树即可维护所有信息，\(O(n+q\log n)\) 解决 . 好麻烦 .

地狱月食

还是献祭了一个 Bomb 打的 .

Dec. 14

讲的树上问题感觉挺好的 .

感觉会一点 puzzle-loop 了 .

绀珠传打到皮丝二非想把页面放大点，但是为什么改分辨率会丢档啊？？ZUN 你咋知道 bug 却不修啊 .

florr 被 HR 带飞了 .

这组数据结构题代码都挺长的不太想全部补掉了，解法大多比较经典，下面是简要题解：

Dec. 15

模拟赛又保龄了，主要是睡太多了没空完善 T1 细节了 /shui

染色

一种合法方案的形态肯定是由若干个没颜色的段隔开，每段都是有至少一个长为 \(k\) 的同色段 .

感知一下合一种同色段的方案是线性递推，合并每个段也是线性递推，所以答案肯定也是线性递推，BM 即可找出递推式 . 实际上仔细写出来原子化的方程然后前缀和优化可以得出答案确实是线性递推 .

接下来倍增处理就好了 .

货车运输

瓶颈路就最大生成树上 Kruskal 重构树，合非树边就是一个树上背包的过程 .

稀疏边集

Dec. 16

DP .

呃呃 .

Dec. 17

THUPC，水了一整天 .

Phigros 和中二联动最后一首那个谱面感觉有潜力竞选愚人节谱 .

Dec. 18

抽象模拟赛，T1 T3 是不可做题，T2 是板题。。。

upd. T3 原来是保序回归啊，这下保序了 .

Dec. 19

happyguy 的 14 道难题.jpg

破防了，4 of 14 跑路了，还有一道是以前讲过的，虽然也有别的可做题但是没心情写了 .

懒得放链接了 . 下面是基本思路完备了的题，别的有一些只胡过的就不写了 .

Bulbasaur

常规解法：扫描线，最大流转为最小割，只需要算 \(dp_{i,S,v}\) 表示第 \(i\) 层点集 \(S\) 为源点流量为 \(v\) 能流到最靠前的层（注意这里隐含了一步值域定义域转换）. 直接做就是 \(\Theta(nk^22^k)\) .

然而能 poly 做，直接看吧，写的挺明白的：

出题人说能 \(O(n\log^2n\operatorname{poly}(k))\)，沈老师说是乱搞 .

Deja Vu

离线下来变成维护一个这种东西：

  • 如果 \(a_i>x\) 就让 \(a_i\gets x\) .
  • 否则如果 \(b_i>x\) 就让 \(b_i\gets x\) .
  • 否则如果 \(c_i>x\) 就让 \(c_i\gets x\) .
  • 否则回答询问 .

seg-beats 就行了，势能分析应该和普通的差不多，最后就是 1 log .

狂暴难写，建议不理 .

Subset Sum Game

略 .

01 Unbalanced

普及题 .

线性听说比较简单，但是我还没想 .

rng_58's Last Problem

last dance .

首先转成矩形上面跳来跳去，这个看图基本就看懂了：

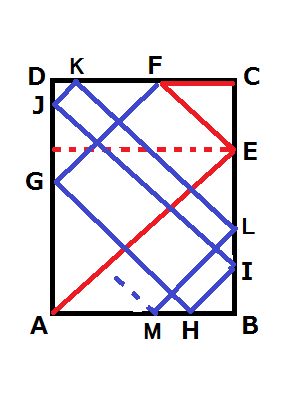
把折着走的部分拍下来变成序列：

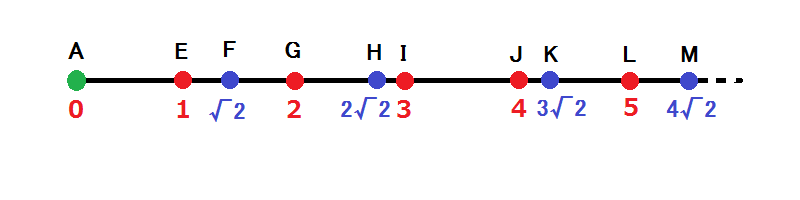
想一下怎么在序列上刻画这个过程，其实就是每次可以在端点处换向，或者直接回 A 点（回 A 点就是横着走到角上）.

单次可以拆成一次走到最远的并走回来的路和若干个出现两次的路拼起来，多次可以拆成一次最远的若干个两次的和若干个单独走有理部和无理部的拼接 .

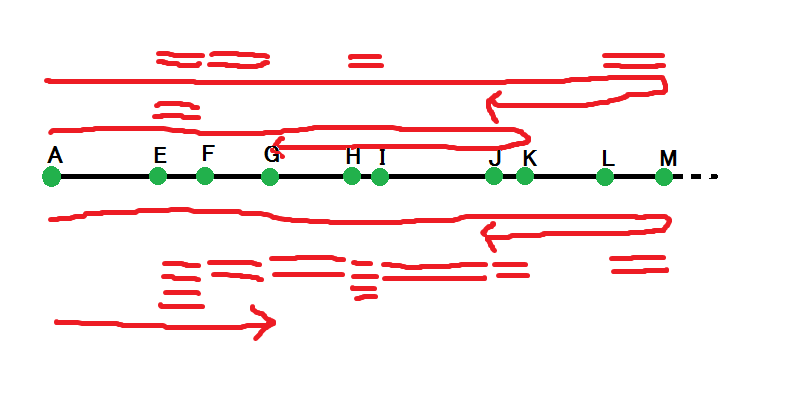
令 \(\{z\}\) 是所有纯有理或无理的 \(\mathbb Z[2]\) 上的数的有序序列，那么如果 \(T\) 合法当且仅当 \(T\) 形如：

\[T=2\cdot z_q-z_p+2\sum_{i=0}^{q-1}(z_{i+1}-z_i)c_i+r+s\sqrt 2 \]

其中 \(p\le q\) .

在复平面状物上看，考察 \(x\le z_q\)，\(\sqrt 2y\le z_q\) 和 \(x+\sqrt 2y\ge 0\) 三个半平面的交：

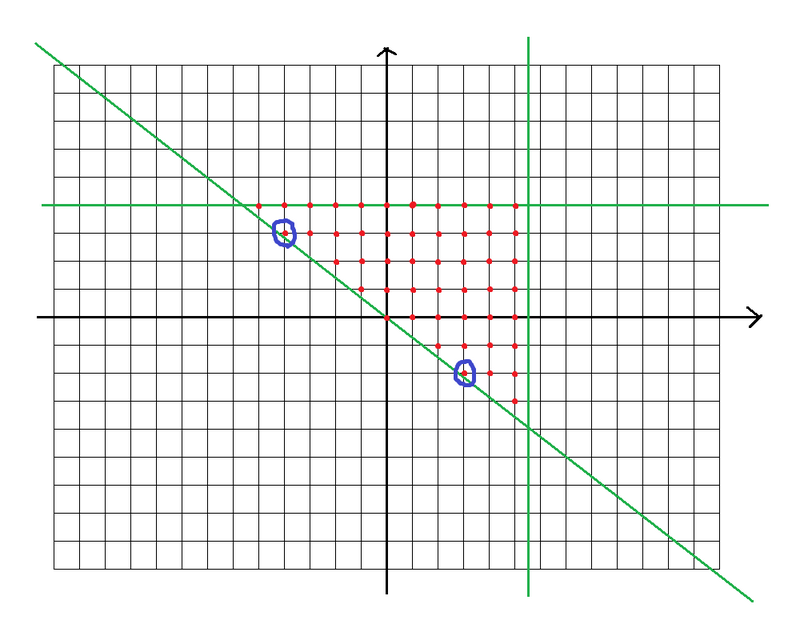
那么红点就表达出了所有 \(z_j-z_i\) .

可以发现如果斜率的极值点和原点的连线上方的位置都行，看图：

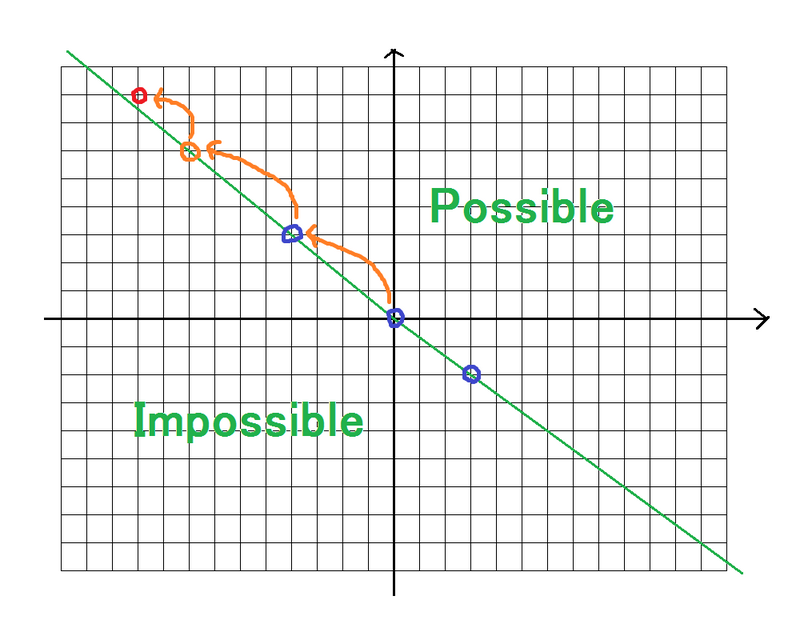
首先初步想法是可以考虑枚举 \(p,q\) 然而并没有什么用，直接 T 飞 .

另外的一些想法是考虑 \(z_q\) 只会有 log 次增加，拆成若干区域后分别处理即可 .

断言：区域对应 \(\sqrt2\) 的有理逼近 .

其实也是比较简单，看图就是 Stern-Brocot Tree 上走，每次走对应一个蓝点，然后直接在上面做就是单次 log 值域的啦啦啦 .

啊啊啊我也太意识流了不过不会有人真的来看这部分文本的吧？？

哈哈哈哈哈做这道题目真的是太快乐了，每一步思考都相当自然而有趣，为出题人点赞！！！

Dec. 20

新年的繁荣：Boruvka，可以不用 Trie 而是 FWT .

Dec. 21

Prefixuffix：挺神奇的题 .

溜大了 .

Dec. 22

模拟赛终于得到了 100 分，感动。。。

下午去 PKU 和 CTT（？）玩，给 zero4338 说了 APJ 科技。

好冷啊 /kel

Dec. 23

说要讲数论，不过讲了一堆别的。看在讲的挺乐的并且还比较有启发性的份上就不攻击了。

集训最终还是结束了啊，各位学长讲的课都非常有趣的。我不禁感叹：stba@bxq#ssdfz。

posted @ 2023-12-10 15:09  Jijidawang  阅读(280)  评论(4)  编辑  收藏  举报
😅​