2023.11.16 闲话

歌：ミマイアイ - Tonbi feat. 鏡音リン .

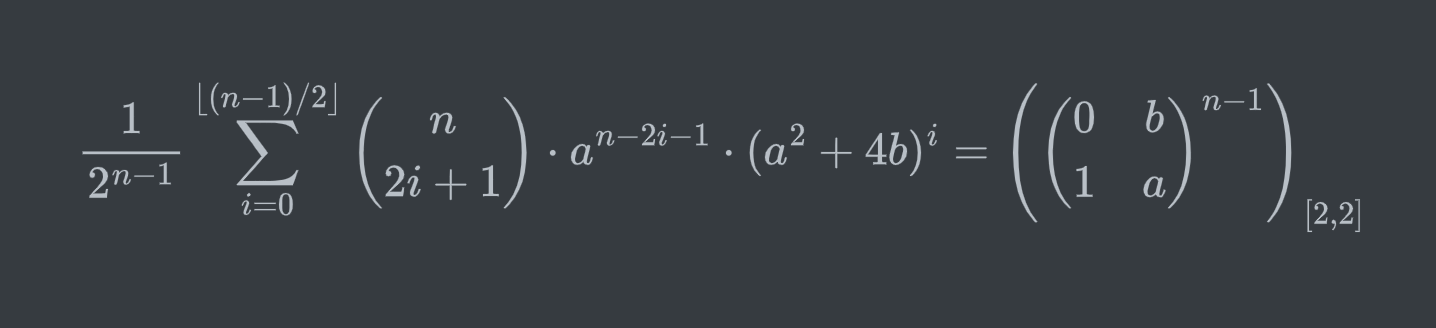
\[\begin{aligned}\begin{aligned}\left(\begin{bmatrix}0&b\\1&a\end{bmatrix}^n\right)_{2,2}&=\dfrac{(a+\phi)^n-(a-\phi)^n}{2^n\cdot \phi}\text{ where }\phi=\sqrt{a^2+4b}\\&=\dfrac1{2^n}\sum_{i=0}^n\dbinom nia^i(\phi^{n-i}-(-1)^{n-i}\phi^{n-i})\\&=\dfrac1{2^n}\sum_{i=0}^{\lfloor n/2\rfloor}\dbinom n{2i+1}a^{n-2i}\phi^{2i}\\&=\dfrac1{2^n}\sum_{i=0}^{\lfloor n/2\rfloor}\dbinom n{2i+1}a^{n-2i}(a^2+4b)^i\end{aligned}&\\&\text{w5.}\end{aligned} \]