2023.10.7 闲话

被 Tibrella D 是现充了呜呜。
被 10circle 说「我觉得作者适合写 SCP。」了,乐。
Tweeting all their lies with hate and vice
Filled with words sharp as a knife, a heart locked from the light
Dressed from head to toe with words of woe
Maybe then you'd like the show, I smile like a ghost
Let's all play a game with hands and string
Mixing thread with wire blades we'll put the cat to sleep
Don't wipe off the blood you're one of us
With that knife still in your hand we'll see just who they trust
Now go
Listen listen, I heard a juicy bit of news
Secret secret, stay Quiet quiet quiet now
Just go
Listen listen, about that girl that no one sees...
Another's pain is so sickeningly sweet
Strained for love in this utopia
Come and try your best to catch me, poet of the loverly
Crooked smiles I wear with disgust
Are just worthless rotting trash that, tie themselves onto me
Hate the same so we're free of the pain
She's the object of our vice, a pitiable sacrifice
Blame, disdain, 'till the target will break
Shift the hatred in our eyes to, whoever is next in line.
Merry bad end
Ha ha ha ha
Tweeting all their lies with hate and vice
Filled with words sharp as a knife, a heart locked from the light
And the secret code that you should know
Is a like and retweet accepting all her posts
Labels on the back that size you up
They all show you're one of us, your usefulness and trust
This one gets a pass and that one too
But be sure that you ignore that one across the room
Gather 'round, gather 'round, everybody gather 'round
Gather 'round, gather 'round, everybody gather 'round
Stop the pain, stop the hate, count your fingers hold them straight
That one pretty fragile girl is not allowed to play
Now go
Listen listen, I heard a juicy bit of news
Secret secret, Quiet quiet quiet now
Just go
Listen listen, a rumor about you know who...
The signal means that the next one up is you
Strained for love in this utopia
Come and try your best to catch me, poet of the loverly
Faking smiles I laugh as I lie
I can't tell the fact from fiction somehow I start to cry
Strained for love in this utopia
It's a cycle never-ending, poet of the loverly
Crooked smiles I wear with disgust
Are just worthless rotting trash that, tie themselves onto me
Where oh where is the eden I seek?
Why does happiness just seem to pour and tumble out of me?
Soon it all will be broken and torn
Not a single soul remains tonight never anymore
Ahh~
Merry bad end
Ha ha ha ha
Itst《浅谈棋盘模型在计数问题中的应用》.
我就按论文的结构写了 . 你的学习笔记就只是把论文抄一遍吗?
定义 \(x^{\underline{n,m}}=x(x-m)(x-2m)\cdots(x-(n-1)m)\) 为 \(x\) 的 \(m\) 阶 \(n\) 次下降幂,\(x^{\overline{n,m}}=x(x+m)(x+2m)\cdots(x+(n-1)m)\) 为 \(x\) 的 \(m\) 阶 \(n\) 次上升幂 .
\(\operatorname{Sym}(n)\) 表示 \(n\) 阶对称群即 \(1\dots n\) 的所有排列 .
对于每个点入出度不超过 1 的有向图 \(G\),\(\operatorname{cycle}(G)\) 表示 \(G\) 的环数 .
例题若无特殊说明则对 \(998244353\) 取模 . 假设长度为 \(n\) 的多项式卷积的时间复杂度为 \(\mathsf M(n)=\Theta(n\log n)\) .
1 定义
\(\textbf{定义 1.1}\text{ (棋盘)}\)
棋盘为一个有限二元组集合 \(S\) 满足对于任意 \((i,j)\in S\) 有 \(i,j\in\N_+\) .
下文中除特殊声明外令 \(n=\max\limits_{(i,j)\in S}i,\,m=\max\limits_{(i,j)\in S}j\) .
\(\textbf{定义 1.2}\text{ (轮廓线棋盘)}\)
对于棋盘 \(S\) 和整数 \(n\),若 \((\max\limits_{(i,j)\in S}i)\le n\) 且对于每个 \(1\le i\le n\) 都存在非负整数 \(a_i\) 使得对于所有 \(k\in\N_+\) 有 \((i,k)\in S\) 当且仅当 \(k\le a_i\),则称 \(S\) 为轮廓线棋盘,记 \(S=F(a_1,a_2,\cdots,a_n)\) .
\(\textbf{定义 1.3}\text{ (Ferrers 棋盘)}\)
对于轮廓线棋盘 \(S=F(a_1,a_2,\cdots,a_n)\),若 \(a_1\le a_2\le\cdots\le a_n\),则称 \(S\) 为 Ferrers 棋盘 . 同时若不存在 \(1\le i<n\) 使得 \(a_i=a_{i+1}\),则称 \(S\) 为严格增 Ferrers 棋盘 . 类似,若 若 \(a_1\ge a_2\ge\cdots\ge a_n\),则称 \(S\) 为减 Ferrers 棋盘 .
这三类棋盘读者应该已经非常熟悉,如图所示,依次为棋盘、轮廓线棋盘和 Ferrers 棋盘:
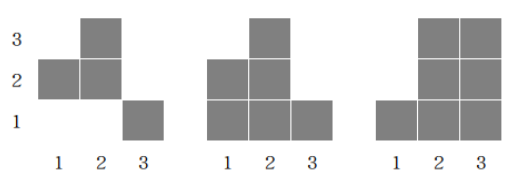
\(\textbf{定义 1.4}\text{ (}k\text{-棋盘数与棋盘多项式)}\)
对于棋盘 \(S\),定义 \(T\subseteq S\) 合法当且仅当对于任意两个不同的二元组 \((p_1,q_1),(p_2,q_2)\in T\) .
定义 \(R_k(S)\) 为 \(S\) 的合法 \(k\) 元子集组成的集合,\(S\) 的 \(k\)-棋盘数 \(r_k(S)=|R_k(S)|\),\(S\) 的棋盘多项式
\[F_S(x)=\sum_{k=0}^{|S|}r_k(S)x^k \]
\(\textbf{定义 1.5}\text{ (}k\text{-命中数)}\)
对于非负整数 \(n\),定义棋盘 \(B_n=\{(i,j)\mid1\le i,j\le n\}\),对于棋盘 \(S\subseteq B_n\),定义 \(H_{k,n}(S)=\{T\in R_n(B_n)\mid |T\cap S|=k\}\),则棋盘 \(S\) 的 \(k\)-命中数 \(h_{k,n}(S)=|H_{k,n}(S)|\) .
上述两种数的组合意义分别如下:
- \(k\)-棋盘数:在棋盘上放置 \(k\) 个互不攻击的车的方案数 .
- \(k\)-命中数:在 \(B_n\) 上放置 \(n\) 个互不攻击的车,且在 \(S\) 上的车有 \(k\) 个的方案数 .
2 基础定理
2.1 棋盘数与命中数的关系
\(\textbf{定理 2.1}\)
对于棋盘 \(S\subseteq B_n\),有
\[\sum_{k=0}^nh_{k,n}(S)x^k=\sum_{k=0}^nr_k(S)(n-k)!(x-1)^k \]
换元 \(x-1\to x\):
提取系数,问题变为证明
考察左式的组合意义,即对于所有命中数 \(\ge i\) 的方案,在命中位置中选 \(i\) 个作为特殊命中位置的方案数之和 . 考虑先枚举这 \(i\) 个特殊位置,选择位置的方案数为 \(r_i(S)\),其他位置可以随便放,就是 \((n-i)!\),从而证得定理 .
2.2 展开定理
\(\textbf{定理 2.2}\text{ (展开定理)}\)
对于非空棋盘 \(S\),取 \((p,q)\in S\),令 \(S_1=S-\{(p,q)\},\,S_2=\{(p_0,q_0)\in S\mid p_0\neq p,q_0\neq q\}\),则:
\[F_S(x)=F_{S_1}(x)+x\cdot F_{S_2}(x) \]
对于每个 \(k\),将 \(R_k(S)\) 分为不包含 \((p,q)\) 的方案集合 \(R_{k,0}(S)\) 和包含 \((p,q)\) 的方案集合 \(R_{k,1}(S)\) . 可以发现 \(R_{k,0}(S)=R_k(S_1)\),在 \(R_{k-1}(S_2)\) 中的每个元素中加入位置 \((p,q)\) 即得 \(R_{k,1}(S)\) .
从而可证得定理 .
2.3 分离定理
\(\textbf{定理 2.3}\text{ (分离定理)}\)
对于棋盘 \(S\) 和 \(S_1\subseteq S\),设 \(S_2=S-S_1\),对于任意 \((p_1,q_1)\in S_1,(p_2,q_2)\in S_2\) 都有 \(p_1\neq p_2\) 且 \(q_1\neq q_2\),则:
\[F_S(x)=F_{S_1}(x)\cdot F_{S_2}(x) \]
条件即为 \(S_1,S_2\) 行列不交 . 从而选择 \(S_1\) 的任一合法子集 \(T_1\) 和 \(S_2\) 的任一合法子集 \(T_2\),可以得到 \(T_1+T_2\) 是 \(S\) 合法子集 . 反之,对于任一 \(S\) 的合法子集可以划分为在 \(S_1\) 内的部分和在 \(S_2\) 内的部分 . 从而建立了 \(S\) 的合法子集和 \(S_1,S_2\) 的合法子集组成的二元组间的双射,从而:
即证得定理 .
3 禁区排列问题
\(\textbf{例题 3.1}\text{ (错排问题)}\)
给定 \(n\),计算:
\[\sum_{\pi\in\operatorname{Sym}(n)}\prod_{i=1}^n[i\neq\pi_i] \]\(1\le n\le 10^7\) .
构造棋盘 \(S=\{(1,1),(2,2),\cdots,(n,n)\}\),所求即为 \(h_{0,n}(S)\),由棋盘数与命中数的关系可得:
直接计算的时间复杂度即为 \(\Theta(n)\) .
\(\textbf{例题 3.2}\text{ (夫妻分座问题)}\)
给定 \(n\) 和两个 \(n\) 阶排列 \(p,q\),对于每个 \(k\in[0,n]\) 计算:
\[\sum_{\pi\in\operatorname{Sym}(n)}\left[k=\sum_{i=1}^n[\pi_i=p_i\lor\pi_i=q_i]\right] \]\(1\le n\le 2\times 10^5\) .
构造棋盘 \(S=\{(i,j)\mid 1\le i,j\le n\land(j=p_i\lor j=q_i)\}\),则所求即为 \(h_{k,n}(S)\),根据棋盘数与命中数的关系转为计算 \(F_S(x)\) .
先考虑考虑 \(p_i=i,q_i=(i\bmod n)+1\) 的特殊情况,即一个环的情况:
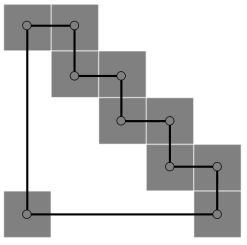
\(r_k(S)\) 即为在环上选 \(k\) 个不相邻点的方案数,这就是 \(r_k(S)=\dfrac{2n}{2n-k}\dbinom{2n-k}k\) .
对于一般情况,原图肯定是若干个环或孤立点的并,分别计算棋盘多项式然后分治乘合并即可 . 对于二项式反演过程也可以使用卷积优化 .
从而得到一个 \(O(n\log^2n)\) 的做法 .
对于 \(p_i=i,q_i=n-i+1\) 的情况是 Permutation .
4 Ferrers 棋盘的棋盘多项式
Ferrers 棋盘是好的 .
4.1 下降幂棋盘多项式分解定理
\(\text{定理 4.1}\text{ (下降幂棋盘多项式分解定理)}\)
对于 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots,a_n)\),有:
\[\sum_{k=0}^nr_k(S)x^{\underline{n-k}}=\prod_{k=1}^n(x+a_k-k+1) \]
因为两侧均为 \(x\) 的多项式所以只需要在无限多点处证明即得原命题成立 .
考察 \(x\in\N\) 的情况 . 如图,令 \(S_x\) 为在 \(S\) 下方加入 \(x\) 行得到棋盘,考虑用两种方法计算 \(r_n(S_x)\) .
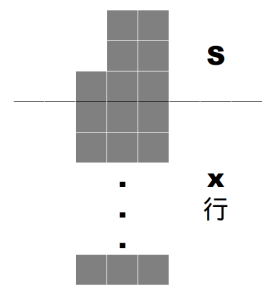
首先可以从左往右一列一列确定每个车放在哪里,显然就是:
其次可以考虑枚举 \(S\) 的合法子集 \(T\),然后计算所有合法方案中与 \(S\) 交集为 \(T\) 的方案数 .
设 \(|T|=k\),那么 \(T\) 中对应的 \(k\) 列不用考虑了,别的列可以用上一种方法的讨论得出,选择子集的方案数就是 \(r_k(S)\),从而:
综合即得 .
由此可以在 \(O(n\log^2n)\) 的时间复杂度内求出任意 Ferrers 棋盘的棋盘多项式 . 一种做法是对于右式分治乘,动态维护下降幂多项式,最后转普通多项式 .
\(\textbf{例题 4.1}\text{ (Gnutella Chessmaster)}\)
对于 \(n\times n\) 的棋盘,对于每个 \(k\in[1,2n)\) 计算在棋盘上放 \(k\) 个互不攻击的国际象棋中的象的方案数 .
\(1\le n\le 10^5\) .
对棋盘进行黑白染色,根据分离定理可以把棋盘拆开考虑 . 对于每种颜色,将棋盘转 \(45^{\circ}\) 就可以转为常见的棋盘模式 .
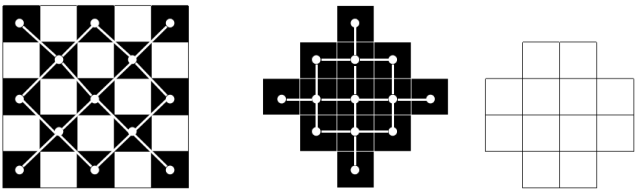
由于交换行列不会改变棋盘的棋盘多项式,所以可以把行列分别按格子数量排序,这样就可以转为 Ferrers 棋盘 . 两种颜色处理方法类似,不妨考虑黑色棋盘 .
黑色棋盘即为 \(F(1,1,3,3,5,5,\cdots)\),使用下降幂棋盘多项式分解定理得:
可以在 \(O(n\log n)\) 的时间复杂度内完成右式的多点求值,卷积即可得到左式多项式系数 .
时间复杂度为 \(\Theta(n\log n)\) .
4.2 阶梯棋盘与斯特林数
\(\textbf{定义 4.1}\text{ (阶梯棋盘)}\)
对于 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots,a_n)\),若对于所有 \(1\le i\le n\) 有 \(a_i=i-1\),则称 \(S\) 为 \(n\) 阶阶梯棋盘,记 \(S=St_n\) .
对 \(St_n\) 应用下降幂棋盘多项式分解定理有:
这指出 \(r_{n-k}(St_n)={n\brace k}\) .
双射
问题:在 \(St_n\) 上放 \(n-k\) 个互不攻击的车的方案数和把 \(n\) 个数划分为 \(k\) 个无序集合的方案数一致 .
对于集合划分 \(S_1,S_2,\cdots,S_k\),将每个集合中的元素从小到大排序 . 设 \(S_i=\{a_1,a_2,\cdots,a_p\}\),则在棋盘的 \((a_2,a_1),(a_3,a_2),\cdots,(a_p,a_{p-1})\) 位置放车即可 .
对于一个 \(n-k\) 个车的合法放车方案,如果有车 \((p,q)\) 则合并 \(p,q\) 所在的集合,即可得到一个合法的集合划分 .
由此建立了集合划分和放车方案的双射 .
\(\textbf{定义 4.2}\)
定义 \(F_k(S)\) 表示在棋盘 \(S\) 上放置 \(k\) 个车使得没有两个车在同一列的所有方案构成的集合,\(f_k(S)=|F_k(S)|\) .
\(f_k(S)\) 与 \(r_k(S)\) 的区别在于没有行的限制 .
\(\textbf{定理 4.2}\)
对于轮廓线棋盘 \(S=F(a_1,a_2,\cdots,a_n)\),有
\[\sum_{k=0}^nf_{n-k}(S)x^k=\prod_{i=1}^n(x+a_i) \]
证明考虑 \(f_k(S)\) 等于 \(\{a_1,a_2,\cdots,a_n\}\) 中选 \(k\) 个数相乘的所有方案之和即可 .
对 \(St_n\) 使用此定理:
这指出 \(f_{n-k}(St_n)={n\brack k}\) .
双射
问题:在 \(St_n\) 上放 \(n-k\) 个不在同一列的车的方案数和把 \(n\) 个数划分为 \(k\) 个圆排列的方案数一致 .
对于一个划分为 \(k\) 个圆排列的方案,对每个排列将最小的元素放在开头 . 依次考虑 \(n\dots1\) . 假设当前考虑 \(i\),若其所在排列中有不止一个元素,则设它前面的元素为 \(v\),加入车 \((i,v)\) . 操作后把 \(i\) 删掉 . 这样即得到一种合法的放车方案 .
同样的,对于一个合法放车方案,按列从小到大考虑,若这一列没有车则新开一个以其为唯一元素的圆排列,否则放在放车的行对应的数字后面 . 这样即可构造一种圆排列划分方案 .
由此建立了圆排列划分和放车方案的双射 .
斯特林反演:
考虑用棋盘理论证明:
\(x=y\) 时容易验证,考察 \(x\neq y\) 时 .
将三元组 \((k,P,Q)\) 分为三类:
- \(P\) 的第 \(y\) 列放了车 .
- \(P\) 的第 \(y\) 列没放车,但 \(Q\) 的第 \(y\) 列放了 .
- \(P\) 的第 \(y\) 列和 \(Q\) 的第 \(y\) 列都没放车 .
可以建立 1 和 2 的反号双射,具体地,对于某个属于 1 类的三元组 \((k,P,Q)\),操作:
- 将 \(P\) 中第 \(y\) 列的车删除得到 \(P'\),并将 \(P'\) 上没有放车的行从下往上从 1 开始编号 .
- 在 \(Q\) 中加入 \((k+1,p)\) 得到 \(Q'\) .
则 \((k,P,Q)\) 对应 \((k+1,P',Q')\),容易验证 \((k,P',Q')\) 属于 2 类,且 \(|Q'|-|Q|=1\) . 逆映射略 .
那么只需要计算第 3 类的贡献:
即将 \(x,y\) 减去 1 答案不变,那么归纳就可以了 .
4.3 棋盘等价类
\(\textbf{定义 4.3}\text{ (棋盘等价)}\)
定义两个棋盘 \(S,T\) 等价当且仅当对于所有 \(i\ge 0\),\(r_i(S)=r_i(T)\) .
对于 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots, a_n)\),在其中加入或删除空列不会影响其 \(k\)-棋盘数,故考虑调整其开头的 0 的数量使得 \(\{a\}\) 的长度为 \(|S|+1\),得到新的棋盘 \(S'=F(a_1',a_2',\cdots,a'_{|S|+1})\),此时定义 \(B_S=\{b_{S,1}=a'_1,b_{S,2}=a'_2-1,\cdots,b_{S,|S|+1}=a'_{|S|+1}-|S|\}\) . 则有:
\(\textbf{定理 4.3}\text{ (Ferrers 棋盘的等价判定)}\)
两个 Ferrers 棋盘 \(S,T\) 等价当且仅当 \(B_S\) 的元素构成的可重集与 \(B_T\) 的元素构成的可重集一致 .
只需要验证其下降幂棋盘多项式相等,然而这是显然的:
得证 .
\(\textbf{引理 4.1}\)
对于 Ferrers 棋盘 \(S=F(a_1,\cdots,a_{|S|+1})\) 和 \(1\le i\le|S|+1\),有 \(b_{S,i}\le 0\) .
假设存在 \(i\) 使得 \(b_{S,i}>0\),即 \(a_i\ge i\),从而根据 Ferrers 棋盘的定义:
不难发现 \((|S|+2-i)i\) 在 \([1,|S|+1]\) 的最小值必然在端点处取到,分别验证即可得到矛盾 .
从而证得引理 .
对于 Ferrers 棋盘 \(S\),令 \(k=-\min b_{S,i}\),考虑将 \(B_S\) 中的元素构成的可重集表为 \(0^{c_0}(-1)^{c_1}\cdots(-k)^{c_k}\) 的形式 .
注意此处所有 \(c_i\) 都不等于 0,因为 \(b_{S,i}-b_{S,i-1}\ge -1\) .
\(\textbf{定理 4.4}\)
对于非空 Ferrers 棋盘 \(S\),恰存在一个不存在空列的严格增 Ferrers 棋盘与 \(S\) 等价 .
设 \(B_S\) 中的元素构成的可重集组成的序列为 \(\{b\}\),那么只需要证明存在一个 \(\{b\}\) 的重排使得 \([b_i\neq1-i]=[b_i\le b_{i+1}]\).
只需要将 \(\{b\}\) 分为一个 \(0\dots-k\) 的递减序列和 \(-k\dots0\) 的不降序列即可得到唯一构造 .
证毕 .
\(\textbf{定理 6.5}\text{ (棋盘等价类大小定理)}\)
对于可重集 \(T=0^{c_0}(-1)^{c_1}\cdots(-k)^{c_k}\),满足 \(B_S\) 中的元素构成的可重集为 \(T\) 的 Ferrers 棋盘 \(S\) 的数量为:
\[\prod_{i=0}^{k-1}\dbinom{c_i+c_{i+1}-1}{c_{i+1}} \]
考虑从 \(T\) 构造出所有的 \(B_S\) .
依次加入 \(0\dots-k\),加入 \(-i\) 时,其前驱肯定是 \(-i\) 或 \(1-i\),所以有 \(c_{i-1}\) 个位置后面的可以放 \(-i\),根据插板法可以得到这里的方案数为 \(\binom{c_{i-1}+c_i-1}{c_i}\),因为每位互相独立所以乘起来就是总方案数了 .
证毕 .
4.4 分解定理的变体
\(\textbf{定义 4.4}\ (m\ 阶\ k\text-棋盘数)\)
对于棋盘 \(S\) 和正整数 \(m\),自下而上将每 \(m\) 行分为一组,则 \(S\) 的 \(m\) 阶 \(k\)-棋盘数 \(r_{m,k}(S)\) 表示在棋盘 \(S\) 上放 \(k\) 个车使得不存在两个车在同一个行组或同一列的方案数 .
可以发现,\(r_k(S)=r_{1,k}(S)\) .
对于 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots,a_n)\),将所有非空列按高度分为若干集合 \(S_1,S_2,\cdots\),其中 \(S_p=\{i\mid a_i\in[pm+1,(p+1)m]\}\)(也就是按照每一列能够放置的最高的行组进行分类),则设 \(\rho_m(S_i)=\sum\limits_{p\in S}a_p-im\) .
\(\textbf{定理 4.6}\ (m\ 阶下降幂棋盘多项式分解定理)\)
对于 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots,a_n)\) 和正整数 \(m\),有:
\[\sum_{k=0}^mr_{m,k}(S)x^{\underline{n-k,m}}=\prod_{i=1}^n(x-(i-1)m+v_i) \]其中:
\[v_i=\begin{cases}0&a_0=0\\pm+\rho_m(S_p)&i\ 是\ S_p\ 的最后一列\\pm&\text{otherwise.}\end{cases} \]
证明和普通的下降幂棋盘多项式分解定理类似,只需要在无穷多个点处考虑,这里考虑 \(m\mid x\) 的 \(x\) .
同样在 \(S\) 下面插入 \(x\) 行得到 \(S_x\)(这里就不放图了,和以前那个一样),用两种方式计算 \(r_{m,n}(S_x)\):
首先可以枚举 \(S\) 的合法子集 \(T\) 并计算与 \(S\) 的交集为 \(T\) 的合法方案数 . 这里不再赘述,答案就是:
其次可以从左到右考虑每个列集合的放车位置 . 对于 \(S_p=[s,t]\) 来说,\(i\in[s,t)\) 列的放车方案数不难发现就是 \(pm+x-(i-1)m\) .
对于第 \(t\) 列,需要额外考虑是否有车放在行组 \([pm+1,(p+1)m]\) 中 . 不放的情况是一样的 . 对于放的情况,在 \(s\dots t-1\) 列的选择中,选择一个位于 \([pm+1, (p+1)m]\) 行组且位于列集合 \(S_p\) 的位置放车 . 若这个放车的位置不在第 \(t\) 列,则将其所在列之前放入的车移动至第 \(t\) 列,这样即得到有车放在 \([pm+1, (p+1)m]\) 行组的一种合法方案 .
容易发现上述变换可逆,从而此时的选择方案数为 \(\rho_m(S_p)\) .
那么每行独立,方案数就是全乘起来:
综合即证得定理 .
\(\textbf{定义 4.5}\ (\alpha\ 权\ k\text-棋盘数)\)
对于棋盘 \(S\) 和实数 \(\alpha\),定义 \(S\) 的 \(\alpha\) 权 \(k\)-棋盘数 \(v_{\alpha,k}(S)\) 表示所有在棋盘 \(S\) 上放 \(k\) 个车使得不存在两个车在同一列的方案的权值和 . 一个放车方案的权值等于其所有行的权值乘积,一行的权值如下定义:
- 若该行上放了不超过一个车,则权值为 1 .
- 否则设放了 \(p\) 个车,则权值为 \(\alpha(2\alpha-1)(3\alpha-2)\cdots(p\alpha-(p-1))\) .
可以注意到 \(v_{0,k}(S)=r_k(S),\,v_{1,k}(S)=f_k(S)\) .
\(\textbf{定理 4.7}\ (\alpha\ 权下降幂棋盘多项式分解定理)\)
对于 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots,a_n)\) 和实数 \(\alpha\),有:
\[\sum_{k=0}^nv_{\alpha,k}x^{\underline{n-k,1-\alpha}}=\prod_{i=1}^n(x+a_i-(i-1)(1-\alpha)) \]
两遍都是关于 \(\alpha\) 的多项式只考虑 \(\alpha\in\N\) 的情况即可 .
断言:对于问题:
给定棋盘 \(S\),从左至右考虑每一列是否放车,若放车则在放车的行上方插入 \(\alpha\) 个空行,后面的列决策时可以选择这些新插入的空行,同时在新插入的空行上放车也会插入空行 .
令此问题中放 \(i\) 个车的方案为 \(v'_{\alpha,i}(S)\) .
有 \(v'_{\alpha,i}(S)=v_{\alpha,i}(S)\) .
考虑构建双射:
- 对于新问题,设某个车在第 \(i\) 列,放在棋盘 \(S\) 的第 \(j\) 行或由其直接或间接插入得到的行,则在原问题棋盘中 \((i, j)\) 位置放车 .
- 对于原问题,若某行有 \(p>1\) 个车,那么构建逆映射后逐个考虑可以得到总方案数与其权值相等 .
证明断言后后面的部分和前面两个下降幂棋盘多项式分解定理的证明方法类似,不多说了 .
\(\textbf{例题 4.2}\text{ (小 Q 的序列)}\)
对于下标从 0 开始的序列 \(\{a_n\}\) 和整数 \(\alpha\),定义一个长为 \(k\) 的序列 \(\{p_k\}\) 的权值为 \(\prod_i(p_i+\alpha i)\) .
对于每个 \(0\le k\le n\) 求 \(\{a\}\) 的所有长为 \(k\) 的子序列的权值和 .
\(1\le n\le 10^5\) .
因为是模 \(p=998244353\) 下考虑的,所以可以适当操作 \(a_i\gets a_i+p\) 以使序列递增 .
对于递增序列 \(\{a\}\),问题想要计算的是 \(F(a_0,a_1,\cdots,a_{n-1})\) 的 \((\alpha+1)\) 权棋盘多项式,设答案为 \(ans_k\) 则可以知道:
首先特判 \(\alpha=0\),否则代入 \(x=-\alpha y\) 最终可以得到:
然后就好做了,时间复杂度 \(O(n\log^2n)\) .
5 排列降低计数
\(\textbf{定义 5.1}\text{ (降低)}\)
对于排列 \(\pi\),定义:
\[\begin{aligned}&Des_{\pi}=\{1\le i<n\mid\pi_i>\pi_{i+1}\}\qquad des_{\pi}=|Des_{\pi}|&\\&Des_{\pi,k}=\{1\le i<n\mid\pi_i-\pi_{i+1}=k\}\qquad des_{\pi,k}=|Des_{\pi,k}|&(k>0)\end{aligned} \]称 \(Des_{\pi}\) 为排列 \(\pi\) 的降低集合,若 \(x\in Des_{\pi}\) 则称 \((\pi_x,\pi_{x+1})\) 为一个降低对,\(des_{\pi}\) 成为 \(\pi\) 的降低;\(Des_{\pi,k}\) 为排列 \(\pi,k\) 的 \(k\)-降低集合,若 \(x\in Des_{\pi,k}\) 则称 \((\pi_x,\pi_{x+1})\) 为一个 \(k\)-降低对,\(des_{\pi,k}\) 成为 \(\pi\) 的 \(k\)-降低 .
\(\textbf{定义 5.2}\text{ (超过数)}\)
对于排列 \(\pi\),定义:
\[\begin{aligned}&Exc_{\pi}=\{1\le i\le n\mid\pi_i>i\}\qquad exc_{\pi}=|Exc_{\pi}|&\\&Exc_{\pi,k}=\{1\le i\le n\mid\pi_i-i=k\}\qquad exc_{\pi,k}=|Exc_{\pi,k}|&(k>0)\end{aligned} \]称 \(Des_{\pi}\) 为排列 \(\pi\) 的超过集合,若 \(x\in Des_{\pi}\) 则称 \((\pi_x,x)\) 为一个超过对,\(des_{\pi}\) 成为 \(\pi\) 的超过数;\(Des_{\pi,k}\) 为排列 \(\pi,k\) 的 \(k\)-超过集合,若 \(x\in Des_{\pi,k}\) 则称 \((\pi_x,x)\) 为一个 \(k\)-超过对,\(des_{\pi,k}\) 成为 \(\pi\) 的 \(k\)-超过数 .
我们可以在 \(\operatorname{Sym}(n)\) 与 \(R_n(B_n)\) 之间建立双射:对于排列 \(\pi\) 在所有 \((i,\pi_i)\) 位置放车 . 在这样的描述方式下,降低由于涉及相邻两个车的位置关系描述较困难,而超过数仅涉及一个车的行列关系更易描述 . 下面将要介绍的对排列的变换将在降低和超过数之间建立联系 .
5.1 Foata 第一基本变换
\(\textbf{定义 5.3}\text{ (Foata 第一基本变换)}\)
对于排列 \(\pi\),对其进行 Foata 第一基本变换即依次进行以下操作得到另一个排列 \(\pi'\):
- 将排列分解为若干个轮换;
- 将每个轮换中的最大值放到轮换末尾,然后按照轮换中的最大值将轮换从小到大排序;
- 将每个轮换翻转起来后拼接得到 \(\pi'\) .
可以发现这个变换是 \(\operatorname{Sym}(n)\to\operatorname{Sym}(n)\) 的双射,因为其逆变换就是按前缀最大值分段后翻转 .
注意到此时 \(\pi\) 中 \((j,i)\) 是一个 \(k\)-超过对当且仅当 \(\pi'\) 中 \((j,i)\) 是一个 \(k\)-降低对 . 因此:
\(\textbf{定理 5.1}\)
\[\begin{aligned}&\sum_{\pi\in\operatorname{Sym}(n)}x^{des_\pi}=\sum_{\pi\in\operatorname{Sym}(n)}x^{exc_{\pi}}\\&\sum_{\pi\in\operatorname{Sym}(n)}x^{des_{\pi,k}}=\sum_{\pi\in\operatorname{Sym}(n)}x^{exc_{\pi,k}}\qquad(k>0)\end{aligned} \]
\(\textbf{例题 5.1}\)
给定 \(n\) 和 \(m\) 个限制,每个限制形如一个二元组 \((i,j)\) 表示排列中 \(i,j\) 相邻且 \(i\) 在 \(j\) 的前面 . 对所有 \(m\le k<n\) 求所有满足限制的 \(n\) 阶排列中升高为 \(k\) 的排列数量 .
\(n\le 10^6\),\(n-m\le 10^5\) . \(\pi\) 的升高定义为 \(\sum[\pi_i<\pi_{i+1}]\) .
首先对于所有 \(\pi\) 中的元素 \(x\) 令 \(x\gets n-x+1\),对于所有限制条件 \((i,j)\) 令 \((i,j)\gets(n-i+1,n-j+1)\),那么对于每一个限制 \((p,q)\) 都有 \(p>q\),需要计算满足所有二元组限制的排列的降低分布 .
考察 Foata 第一基本变换的逆变换过程可以得到逆变换后得到的排列 \(\pi'\) 中限制形如 \(\pi'_q=p\) .
那么问题转为计算给出若干位置的排列的超过数的分布 . 对于没有限制的情况可以构建棋盘模型:
考虑如图所示的倒三角棋盘:

若其中黑色棋盘为 \(S_n\),则答案即为 \(h_{k,n}(S_n)\) .
对于有限制的情况对于每个限制 \((p,q)\) 删掉第 \(p\) 行和第 \(q\) 列后重标号 . 对于固定的部分可以 \(\Theta(m)\) 扫一遍解决,其余部分同上 .
关于计算 \(h_{k,n}(S_n)\),转 \(180^{\circ}\) 就是 Ferrers 棋盘,然后就好做了 .
从而问题被 \(\Theta(m+(n-m)\log^2(n-m))\) 解决 .
尝试考察没有限制的情况,即求:\(\sum_{\pi}[exc_{\pi}=k]\),因为有双射所以求的就是欧拉数,同时用类似的变换可以转为计算 \(h_{k,n}(S_n)\),转 \(180^{\circ}\) 就是要算 \(r_k(St_n)\),这个前面已经讨论了就是第二类斯特林数,所以总结一下就得到:
5.2 \(k\)-超过数计数
设 \(P_{n,k,p}=\sum\limits_{\pi\in\operatorname{Sym}(n)}[exc_{\pi,k}=p]\),那么就是要计算 \(h_{p,n}(S_{n,k})\) 其中棋盘 \(S_{n,k}=\{(1,k+1),(2,k+2),\cdots,(n-k,n)\}\) . 因为 \(S_{n,k}\) 的格子两两不在同行或同列,所以 \(r_i(S_{n,k})=\binom{n-k}i\),进而有:
\(\textbf{定理 5.2}\)
\[P_{n,k,p}=\sum_{i=p}^{n-k}(-1)^{i-p}\dbinom ip\dbinom{n-k}i(n-i)! \]
\(P_{n,k,p}\) 还有一些有趣的性质:
\(\textbf{定理 5.3}\)
对于 \(0\le k<n\),\(p\ge 1\):
\[P_{n,k,p}=P_{n-1,k,p-1}+(p+1)P_{n-1,k,p+1}+(n-p+1)P_{n-1,k,p} \]
考虑在 \(\pi\in\operatorname{Sym}(n-1)\) 上按如下方式加入 \(n\) 得到 \(n\) 阶排列 \(\pi'\):先将 \(n\) 放在 \(\pi\) 最后,然后
选择一个位置 \(i\),若 \(i\neq n\) 则交换 \(\pi_i\) 和 \(n\) 得到 \(\pi'\) .
考虑该过程的三种结果:
- \(\pi'_{n-k}=n\),即 \(exc_{\pi',k}=exc_{\pi,k}+1\) . 此时只有 \(i=n-k\) 合法,方案数为 \(P_{n-1,k,p-1}\) .
- \(\pi'_n=i+k\),即 \(exc_{\pi',k}=exc_{\pi,k}-1\) . 此时 \(p+1\) 个超过位置都是合法的 \(i\),方案数为 \((p+1)P_{n-1,k,p+1}\) .
- 其他情况,即 \(exc_{\pi',k}=exc_{\pi,k}\) . 此时 \(n-1-p\) 个没有贡献不是 \(n-k\) 的位置都是合法的 \(i\),方案数为 \((n-p+1)P_{n-1,k,p}\) .
从而可以证明定理 .
对于 \(p=0\) 处的情况,有补充:
\(\textbf{定理 5.4}\)
对于 \(0\le k<n\):
\[P_{n,k,0}=(n-1)P_{n-1,k,0}+(n-k-1)P_{n-2,k,0} \]
沿用和上一个定理类似的方法考虑:
- \(exc_{\pi,k}=0\),此时 \(i\neq n-k\) 就合法,方案数为 \((n+1)P_{n-1,k,0}\) .
- \(exc_{\pi,k}=1\),此时仅有一个 \(i\) 合法,对于这样的排列 \(\pi\),在棋盘 \(S_{n-1,k}\) 上将命中的格子所在行列删掉然后重标号 . 那么可以构建映射,进而得到方案数为 \((n-k-1)P_{n-2,k,0}\) .
从而可以证明定理 .
\(\textbf{定理 5.5}\)
对于 \(0\le k\le n\):
\[P_{n,k,0}=k!\sum_{r=0}^k\dbinom kr\dbinom{n-k}{k-r}P_{n-k,k-r,0} \]
考虑 \(S_{n,k}\) 中最后 \(k\) 列的情况,枚举其中放在 \(1\dots k\) 行中车的数量 \(r\),那么删掉它们后不会有什么影响,删掉剩余的 \(k-r\) 个车时会顺便删掉一个格子 . 此时的方案数为 \(\binom kr\binom{n-k}{k-r}k!\) .
对于剩下的部分,新的棋盘也是任意两个格子不同行或同列的棋盘,并且规模更小,容易得到方案数为 \(P_{n-k,k-r,0}\) .
综合可证得定理 .
\(\textbf{定理 5.6}\)
\[P_{n,k,s}=\dbinom{n-k}sP_{n-s,k,0} \]
考虑枚举命中棋盘 \(S_{n,k}\) 的位置的个数 \(s\) 即可 .
5.3 \(X-Y\) 降低计数
\(\textbf{定义 5.4}\)
给定数集 \(X,Y\),对于 \(n\) 阶排列 \(\pi\),定义:
\[\begin{aligned}&Des_{\pi,X,Y}=\{1\le i<n\mid\pi_i>\pi_{i+1},\pi_i\in X,\pi_{i+1}\in Y\}\qquad des_{\pi,X,Y}=|Des_{\pi,X,Y}|\\&Exc_{\pi,X,Y}=\{1\le i\le n\mid\pi_i>i,\pi_i\in X,i\in Y\}\qquad exc_{\pi,X,Y}=|Exc_{\pi,X,Y}|\end{aligned} \]称 \(Des_{\pi,X,Y}\) 为排列 \(\pi\) 的 \(X-Y\) 降低集合,若 \(x\in Des_{\pi,X,Y}\) 则称 \((\pi_x,\pi_{x+1})\) 为一个 \(X-Y\) 降低对,\(des_{\pi,X,Y}\) 称为 \(\pi\) 的 \(X-Y\) 降低 . 称 \(Exc_{\pi,X,Y}\) 为排列 \(\pi\) 的 \(X-Y\) 超过集合,若 \(x\in Exc_{\pi,X,Y}\) 则称 \((\pi_x,x)\) 为一个 \(X-Y\) 超过对,\(exc_{\pi,X,Y}\) 称为 \(\pi\) 的 \(X-Y\) 超过数 .
通过 Foata 第一基本变换可以得到 \(des_{\pi,X,Y}\) 与 \(exc_{\pi,X,Y}\) 的双射:
\(\textbf{定理 5.7}\)
对于 \(X,Y\subseteq[1,n]\cap\Z\),有:
\[\sum_{\pi\in\operatorname{Sym}(n)}x^{des_{\pi,X,Y}}=\sum_{\pi\in\operatorname{Sym}(n)}x^{exc_{\pi,X,Y}} \]
计算 \(exc_{\pi,X,Y}\) 仍然可以使用棋盘模型,令 \(S_{X,Y}=\{(i,j)\mid i\in Y,j\in X,i<j\}\),则:
对于棋盘 \(S_{X,Y}\),按照格子个数从小到大排序,可以得到一个 Ferrers 棋盘,从而可以根据定理 4.4 得到:
\(\textbf{定理 5.8}\)
对于任意数集 \(X,Y\) 存在恰一个数集 \(X'\) 使得:
\[\sum_{\pi\in\operatorname{Sym}(n)}x^{des_{\pi,X,Y}}=\sum_{\pi\in\operatorname{Sym}(n)}x^{des_{\pi,X',\N}} \]
对于 \(\sum_{\pi\in\operatorname{Sym}(n)}\limits[des_{\pi,X,Y}=p]\) 的计算,可以参考 John T. Hall and Jeffrey B. Remmel. Counting descent pairs with prescribed tops and bottoms. Journal of Combinatorial Theory, 115(5):693–725, 2008.
6 Ferrers 棋盘的排列逆序对计数
轮廓线棋盘排列逆序对个数和:AGC023E Inversion .
下面介绍 Ferrers 棋盘上的情况 . 省流就是把原问题扩展到 \(q\)-analogue 就解决了 .
6.1 \(k\)-棋盘数的 \(q\)-analogue 形式
\(q\)-analogue 大家应该都熟,放两个定义先:
\(\textbf{定义 6.1}\text{ (棋盘放车方案的权值)}\)
对于 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots,a_n)\subseteq B_n\) 和任一合法放车方案 \(T\subseteq S\),对于 \(T\) 中的每一个车 \((i,j)\),在棋盘 \(S\) 中对所有满足 \(i<k\le n\) 的位置 \((k,j)\) 和所有满足 \(1\le k<j\) 的位置 \((i,k)\) 打上标记,记 \(C_S(T)\) 为操作后 \(S\) 上没有被打标记且没有放车的格子,则定义 \(T\) 在 \(S\) 中的权值 \(val_S(T)=|C_S(T)|\) .
(注:大部分英文文献将其称之为为逆序对数 \(inv\))
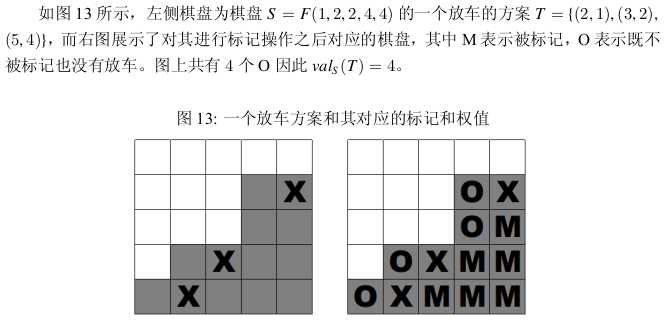
\(\textbf{定义 6.2}\text{ (正序对和逆序对)}\)
对于排列 \(\pi\in\operatorname{Sym}(n)\),定义:
\[coinv_{\pi}=|\{(i,j)\mid i<j,\pi_i<\pi_j\}|\qquad inv_{\pi}=|\{(i,j)\mid i<j,\pi_i>\pi_j\}| \]分别表示排列 \(\pi\) 的正序对数和逆序对数 .
\(\textbf{定理 6.1}\)
对于排列 \(\pi\in\operatorname{Sym}(n)\) 和 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots,a_n)\subseteq B_n\),若 \(T=\{(i,\pi_i)\mid 1\le i<n\}\subseteq S\),则:
\[val_S(T)+\sum_{i=1}^n(n-a_i)=coinv(\pi) \]
证明考虑左式即计算没有被标记的格子的数量,考虑构建双射:对于一个没有被标记且没有放车的格子 \((i,j)\),考察二元组 \((i,\pi_j^{-1})\) 即可 .
同时有 \(coinv(\pi)+inv(\pi)=\binom n2\),所以也可以构建 \(inv(\pi)\) 与 \(val_S(T)\) 的关系 .
\(\textbf{定义 6.3}\ (k\text-棋盘数的\ q\text{-analogue}\ 形式)\)
对于 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots,a_n)\subseteq B_n\) 定义 \(S\) 的 \(q\)-analogue \(k\)-棋盘数:
\[[r_k(S)]_q=\sum_{T\in R_k(S)}q^{val_S(T)} \]
\(q=1\) 时即为 \(k\)-棋盘数 \(r_k(S)\) .
6.2 \(q\)-analogue 形式下的分解定理
\(\textbf{定理 6.2}\ (q\text{-analogue 下降幂棋盘多项式分解定理})\)
对于 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots,a_n)\):
\[\sum_{k=0}^n[r_k(S)]_q[x]_q^{\underline{n-k}}=\prod_{i=1}^n[x+a_i-i+1]_q \]
只需要在 \(x\in\N\) 处证明,\(S\) 下面加 \(x\) 行得到 \(S_x\),计算 \([r_n(S_x)]_q\):
首先可以一列一列考虑,对于第 \(i\) 列每个格子上面的所有格子可以给权值提供贡献所以第 \(i\) 列的贡献就是 \([x+a_i-i+1]_q\),乘起来即得:
另一方面考虑枚举 \(S\) 的合法子集 \(T\),计算所有合法方案中与 \(S\) 交集为 \(T\) 的方案的权值和 . 设 \(|T|=k\) 那么一列一列考虑可以得到 \(T\) 的贡献时 \(q^{val_S(T)}[x]_q^{\underline{n-k}}\),从而可得:
综合即证得定理 .
考虑代入 \(x=0\):
\(\textbf{引理 6.1}\)
对于 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots,a_n)\):
\[[r_n(S)]_q=\prod_{i=1}^n[a_i-i+1]_q \]
这样就得到了 \([r_n(S)]_q\) 的封闭形式,也可以得到 \(q\)-analogue \(k\)-命中数
的封闭形式 . 直接代入 \(q\) 即可计算满足条件的逆序对带权和在 . 对 \(q\) 求导代入 \(q=1\) 即可计算满足条件的逆序对的个数和 .
同时注意到 \(coinv(\pi)=inv(\overline{\pi})\),故对于减 Ferrers 棋盘也有类似的公式 .
7 Ferrers 棋盘的排列环数计数
7.1 有向图的覆盖多项式
对于棋盘 \(S\),若 \((i,j)\in S\) 则连边 \(i\to j\),从而可以从棋盘构建有向图 .
\(\textbf{定义 7.1}\text{ (有向图的覆盖多项式)}\)
对于 \(n\) 个点的有向图 \(G\),定义其覆盖多项式:
\[C(G,x,y)=\sum_{p\ge 0}\sum_{q\ge 0}c_G(p,q)x^{\underline p}y^{\underline q} \]其中 \(c_G(p, q)\) 表示用恰好 \(p\) 条链和恰好 \(q\) 个环覆盖所有点恰好一次的方案数,两个覆盖方案不同当且仅当使用的边集不同 .
\(\textbf{定理 7.1}\)
对于棋盘 \(S\subseteq B_n\),设有向图 \(G\) 为棋盘 \(S\) 对应的有向图,则:
\[C(G,x,1)=\sum_{k=0}^nr_k(S)x^{\underline{n-k}} \]
对比下降幂处的系数则只需要证明:
考虑构建双射,容易发现 \(n-k\) 条链的链覆盖和放 \(k\) 个车的方案构成双射 . 从而可以证明定理 .
这意味着可以通过覆盖多项式来求解棋盘多项式 . 同时可以发现覆盖多项式实际上是棋盘多项式的推广,相比棋盘多项式其在环数上也进行了记录,即 \(c_G(p, q)\) 表示的就是在棋盘 \(S\) 上放 \(n-p\) 个车使得对应到图上有 \(q\) 个环的方案数 .
\(\textbf{例题 7.1}\text{ (棋盘多项式计算)}\)
给定 \(n\) 和棋盘 \(S\subseteq B_n\),对于每个 \(T\subseteq[1,n]\cap\Z\) 求 \(S_T=\{(i,j)\in S\mid i,j\in T\}\) 的棋盘多项式 .
\(n\le 15\),\(|S|\le n\times n\) .
设 \(S\) 对应的有向图为 \(G\),问题即计算 \(G\) 的所有导出子图在 \(y=1\) 处的覆盖多项式 .
首先考虑计算 \(f_T,g_T\) 表示覆盖点集 \(T\) 的链和环的数量 . 考虑 DP,对于 \(f\) 比较简单,对于 \(g\) 令 \(dp_{T,j}\) 表示覆盖点集 \(T\)、起点为 \(T\) 编号最小的点、终点为 \(j\) 的一条链,最后考虑终点到起点是否有边即可 . 此处总时间复杂度为 \(O(2^nn^2)\) .
设 \(P_T=xf_T+g_T\),\(Q_T\) 表示 \(T\) 的所有划分的 \(P\) 乘积和,则可以得到 \([z^{\underline k}]Q_T=r_{|T|-k}(S_T)\) .
变换 \(P\to Q\) 即为集合幂级数的 exp,可以考虑代入点值 \(x=0\dots n\) 每次计算一元 exp 然后插值回去 .
总时间复杂度 \(O(2^nn^3)\) .
7.2 Ferrers 棋盘覆盖多项式分解定理
因为上述双射时 \(S\subseteq B_n\) 的时候成立的,所以 \(S\) 行列相差较大时并不适于考虑,因此对棋盘额外定义覆盖多项式是必要的 .
\(\textbf{定义 7.2}\text{ (棋盘与放车方案的对应图)}\)
对于一个棋盘或放车方案 \(S\),按如下过程构造其对应图 \(G_S\):
- \(G_S\) 包含所有编号属于 \(\Z\) 的点 .
- 对于 \((i,j)\in S\),\(G_S\) 中有边 \(i\to j\),否则没有边 .
\(\textbf{定义 7.3}\text{ (棋盘的覆盖多项式)}\)
定义所有元素的列标号不大于 \(n\) 的棋盘 \(S\) 的覆盖多项式
\[C(S,x,y)=\sum_{i=0}^n\sum_{j\ge 0}r_{i,j}(S)x^{\underline{n-i}}y^j \]其中 \(r_{i,j}(S)\) 表示在棋盘 \(S\) 上放 \(i\) 个车的合法方案中对应图的环数为 \(j\) 的方案数 .
\(\textbf{定理 7.2}\text{ (Ferrers 棋盘覆盖多项式分解定理)}\)
对于 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots,a_n)\subseteq B_n\):
\[C(S,x,y)=\prod_{a_i\ge i}(x+a_i-i+y)\prod_{a_i<i}(x+a_i-i+1) \]
只需要在 \(x\in\N\) 处证明,\(S\) 下面加 \(x\) 行(编号为 \(0\dots1-x\))得到 \(S_x\) . 考虑计算 \(\sum\limits_{T\in R_n(S_x)}y^{\operatorname{cycle}(G_T)}\) .
首先可以枚举 \(S\) 的合法子集 \(T\),计算所有合法方案中与 \(S\) 交集为 \(T\) 的方案贡献和 . 显然可以得到:
另一方面可以一列一列考虑,由 Ferrers 棋盘的性质可得对于 \(a_i\ge i\) 时立即成环否则不成环 . 从而可以得到:
综合即证得定理 .
下一章是在减 Ferrers 棋盘上的拓展 .
7.3 分解定理在减 Ferrers 棋盘上的扩展
如果想考察减 Ferrers 棋盘上的覆盖多项式分解定理,一列一列考虑时,对于 \(a_i\ge i\) 的情况在原命题中总是存在一个位置放车之后可以成环,但减 Ferrers 棋盘上这不总是能够实现的,因为在减 Ferrers 棋盘中对于 \(i<j\),如果 \((j,i)\in S,\,(i,i)\in S\),并不能推出 \((i,j)\in S\) .
先考察对于 \(i<j\),\((j,i)\in S,\,(i,i)\in S\) 能推出 \((i,j)\in S\) 的减 Ferrers 棋盘 .
\(\textbf{定义 7.4}\text{ (竖直型减 Ferrers 棋盘)}\)
定义减 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots,a_n)\) 是竖直型减 Ferrers 棋盘当且仅当对于任意 \(i,j\),\((j,i)\in S\) 可以推出 \((i,j)\in S\) .
\(\textbf{定理 7.3}\text{ (竖直型减 Ferrers 棋盘覆盖多项式分解定理)}\)
对于竖直型减 Ferrers 棋盘 \(S=F(a_1,a_2,\cdots,a_n)\),有:
\[C(S,x,y)=\prod_{a_i\ge i}(x+a_i-(n-i)+y-1)\prod_{a_i<i}(x+a_i-(n-i)) \]
证明和定理 9.2 类似,只需要从右往左考虑每一列即可 .
对于任意减 Ferrers 棋盘 \(S\),对格子 \((i,j)\in S\) 编号 \(\min\{i,j\}\),此时编号相同给定格子构成 L 形 . 考虑对于每个下端长于左端的 L 形交换下端和左端的长度,得到新的棋盘,如图:
断言:减 Ferrers 棋盘进行翻转操作之后得到的是一个竖直型减 Ferrers 棋盘;翻转操作前后覆盖多项式不变 .
下面将依次证明这两个断言 .
\(\textbf{引理 7.1}\)
棋盘 \(S\) 是减 Ferrers 棋盘当且仅当对所有在棋盘中的格子 \((i, j)\) 编号 \(\min\{i,j\}\) 后相同编号的格子构成一个 L 形,且若左端长度为 \(p_i\),下端长度为 \(q_i\),则 \(\forall p_i\neq0,p_i>p_{i+1},q_i>q_{i+1}\) .
前一部分是平凡的,对于存在某一个编号不构成 L 形的棋盘,一定存在某行或某列不满足恰有一段前缀的格子属于 \(S\) ,因此 \(S\) 一定不是减 Ferrers 棋盘 .
考虑按照编号从大到小加入每一个 L 形并维护每一列的高度,设仅考虑编号 \(\ge i+1\) 的格子构成的棋盘为 \(F(a_1,a_2,\cdots,a_{q_i+1})\),加入一个编号为 \(i\) 的 L 形相当于对 \(\{a\}\) 的一个长为 \(q_i-1\) 的前缀加一,最后在序列最前面插入一个 \(p_i\) .
那么此时同时满足以下两个条件是新棋盘是减 Ferrers 棋盘的充要条件:
- \(q_i>q_{i+1}\),否则将不满足 \(q_{i+1}\) 列恰有一段行前缀属于 \(S\) .
- \(p_i>p_{i+1}\),否则将不满足 \(\{a\}\) 单调不增 .
即证明引理 .
\(\textbf{定理 7.4}\)
对减 Ferrers 棋盘进行翻转操作后得到的棋盘一定是减 Ferrers 棋盘 .
对于相邻的两个编号 \(i,i+1\),只有编号为 $i 的 L 形不翻转,编号为 \(i+1\) 的 L 形翻转是非平凡情况,此时交换之后有 \(p_i>q_i>q_{i+1}\),\(q_i>q_{i+1}>p_{i+1}\),所以这两个 L 形仍然满足构成减 Ferrers 棋盘的条件 .
证明完毕 .
同时因为翻转过后棋盘满足 \(p_i\ge q_i\),所以同时它也是竖直型减 Ferrers 棋盘 .
\(\textbf{定理 7.5}\)
对于减 Ferrers 棋盘 \(S\) 和其翻转得到的竖直型减 Ferrers 棋盘 \(S'\) ,设集合 \(P_S\) 表示 \(G_S\) 中的所有简单有向链和简单环构成的集合,则存在一个双射:
\[\phi:P_S\to P_S \]使得若 \(T\in P_S\),则:
- \(\phi(T)\) 和 \(T\) 覆盖相同的点集 .
- \(\phi(T)\) 是简单环当且仅当 \(T\) 是简单环 .
考虑对 \(v=\max_{p_i>0}i\) 归纳 . 当 \(v=0\) 时 \(\phi(\{v\})=\{v\}\) 即满足条件 .
当 \(0\dots v-1\) 结论均成立时,考虑对于棋盘 \(S,S'\),将编号为 1 的格子删掉得到棋盘 \(S_0,S_0'\) 满足 \(S_0'\) 是 \(S_0\) 翻转得到的,从而存在双射 \(\psi:P_{S_0}\to P_{S_0'}\) 满足条件 . 加入编号为 1 的格子可看做在对应图上插入编号为 1 的点,原编号为正的点编号加一,然后从 1 向一段正整数的前缀连边,从另一段正整数的前缀向 1 连边,自环不重复连接 .
对于 \(T\in P_S\),若 \(T\in P_{S_0}\) 则 \(\phi(T)=\psi(T)\),若 \(T=\{1\}\) 则 \(\phi(T)=T\),否则考虑 1 在 \(T\) 中的情况以及 \(S\) 变为 \(S'\) 的过程中是否翻转编号为 1 的 L 形,可以得到对应 \(\phi(T)\) 的取值:
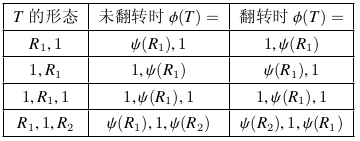
其中 \(R_1,R_2\) 为 \(P_{S_1}\) 中的某条简单有向链,逗号连接表示顺次首尾相连 .
容易验证 \(\phi\) 的一对原像和像满足同时不是环或同时是环,且构成它们的点集是一致的,故只需要证明这样的连边不会导致某条边不属于 \(S'\) 即可:
- 对于 \(R_1\) 或 \(R_2\) 大小 \(\le 1\) 的情况,其在 \(\psi\) 下的像为其本身,不难发现边是存在的 .
- 对于 \(R_1\) 或 \(R_2\) 大小 \(>1\) 的情况,可以利用减 Ferrers 棋盘的直接推论“从 1 能直接到达以及能直接到达 1 的集合总是其他点的对应集合的超集”论证,具体使用反证法,然后考察一个 \(\psi(R)\) 的起始/终止节点 \(w\) 即可 .
证明完毕 .
从而断言已被完全证明,综合可得:
\(\textbf{定理 7.6}\)
对于任意减 Ferrers 棋盘,存在一个竖直型减 Ferrers 棋盘与其拥有相同的覆盖多项式 .
那么减 Ferrers 棋盘的覆盖多项式就好做了 . 放一道 Itst 的互测神题:
\(\textbf{例题 7.2}\text{ (数圈圈)}\)
给定整数 \(n,y\) 和一个长度为 \(n\) 的整数序列 \(\{a_n\}\),保证序列单调不减或单调不增 .
构建有向图 \(G(V,E)\),其中 \(V=\{1,2,\cdots,n\}\),\(E=\{(i,j)\mid a_i\ge j\}\) .
定义边子集 \(T\subseteq E\) 合法当且仅当图 \(G'(V,T)\) 中每个点的入度和出度不超过 1,自环对对应点的入度和出度均贡献 1 . 定义一个合法边子集 \(T\) 的权值为 \(y^{\operatorname{cycle}(T)}\) . 我们认为 \(0^0=1\) .
对于所有 \(0\le k\le n\),求所有大小为 \(k\) 的合法边子集的权值和 .
\(1\le n\le 10^5\),\(0\le a_i\le n\),\(0\le y<998244353\) .
我想你已经会做了 .
以下是博客签名,正文无关
本文来自博客园,作者:yspm,转载请注明原文链接:https://www.cnblogs.com/CDOI-24374/p/17744770.html
版权声明:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议(CC BY-NC-SA 4.0)进行许可。看完如果觉得有用请点个赞吧 QwQ


 浙公网安备 33010602011771号
浙公网安备 33010602011771号