破环为链

处理环上问题一般要考虑把它转换为链上问题，比如复制一遍那么每个长为 \(n\) 的段就是一个循环移位，或者枚举从哪里断开变成一条链。

总之如果有一个非常优秀的结构，首先它得有一个环，然后你在环的每一个点外挂一棵树。结果你造出了一棵基环树。我一直对基环树抱有较低的评价，因为找环需要一次 DFS，DFS 是坏的。

对于一棵基环树，或许你可以随便找一个点把它断开然后合并两边的方案，这时候一般使用 DP 进行处理。不过如果把它断开之后，假设形成的是顺次连接的树 \(\mathcal T_{1\dots k}\)，那么把它复制一遍变成 \(\mathcal T_{1\dots k}\mathcal T_{1\dots k}\)，它的任意一个长度为 \(k\) 的子串都是环的一种走法。不过这些是两两同构的所以没有什么意义。

如果对其 DFS 树进行考虑，也有非常好的性质。基环树总是欧几里得空间，所以你可以在下层叙事观测它。假如你要解决经典的「最大权独立集」问题（注意这个题目和 E_Space 没有任何关系），那么令 \(f(u)\) 表示 \(u\) 所在环对应 DFS 树上深度最大的点，则令 \(dp_{u,0/1,0/1}\) 表示处理到 DFS 树上点 \(u\) 的子树，\(u\) 选 / 不选和 \(f(u)\) 选 / 不选的答案，这样就可以了。它也相当于把环直接拆开了。

对于一个环 \(C\) 来说，如果顺次观测它的每一个点 \(u_k\)，那么把 \(\{u\}\) 复制一遍可以得到序列 \(U^2\)，它的任意子串都是 \(C\) 的一个循环移位。这是好的吗？如果你要在 \(C\) 上行走，这就是不好的，因为它得到的事实上还是一个环 \(C'\)。令这样得到的环为 \(C\) 的倍增，记作 \(\operatorname{doub}(C)\)。如果你对序列 \(U\) 考察 \(U^k\)，事实上也是可以构建出环的体系的。这些被称为环的「扩张」。那 \(U^{\infty}\) 呢？

\(\textbf{定义 1.1}\ (环的扩张)\)

对于一个环 \(C\)，如下定义 \(C\) 的扩张 \(\operatorname{span}(C)\)：

• \(C\in\operatorname{span}(C)\)。
• \(\forall C_0\in\operatorname{span}(C),\,\operatorname{doub}(C_0)\in\operatorname{span}(C)\)。
• \(\forall C_0,C_1\in\operatorname{span}(C),\,C_0C_1\in\operatorname{span}(C)\)。

你会发现一个扩张 \(C^k\in\operatorname{span}(C)\) 可能有多种表示方式，它可以被简单刻画为「有标号 2 的幂次划分」。

回到最初的部分，如果基环树 \(G\) 是有标号的，或者仅仅是它的环是有标号的，那么，对于环 \(C=\operatorname{cycle}(G)\) 来说，你可以操作它的扩张 \(\operatorname{span}(C)\)，这样它确实变成了森林上的问题。

\(\textbf{定义 1.2}\ (基环树的平铺)\)

对于一个基环树 \(G(V,E)\)，其平铺 \(\operatorname{flat}(G)(V',E')\) 定义为：

• \(\operatorname{flat}(G)\) 是一棵树。
• \(V'=V\)。
• \(|E'\setminus E|=1\) 且 \(|E'\setminus E|\in\operatorname{cycle}(G)\)。

\(\textbf{定义 1.3}\ (基环树的展开)\)

对于一个基环树 \(G\)，其展开 \(\operatorname{unfold}(G)\) 定义为：

• \(\operatorname{flat}(G)\in\operatorname{unfold}(G)\)。
• \(\forall G_0\in\operatorname{unfold}(G),\,G\star \operatorname{span}(\operatorname{cycle}(G_0))\in\operatorname{unfold}(G)\)。

很自然的 \(\mathbb{CYCLE}\to\mathbb{TREE}^{+}\) 的推广是定义 \(\operatorname{doub}(G)\) 表示 \(G\) 的倍增，这里不再展开定义。

哦，梦幻。我仍记得，是那个 freopen 题来着。

不难发现，取 \(\operatorname{cycle}(\operatorname{doub}(G))\) 的每个长度为 \(|\operatorname{cycle}(G)|\) 的子串，最终可以得到每个循环移位，这也就刻画了有标号的基环树，转为森林的结构。

下面，记所有取任何组合类 \(A\) 倍增子串得到的组合类为 \(\operatorname{chain}(A)\)。

事实上，这些内容并不一定要局限在组合类上，如果在欧几里得空间上考虑（这可能是一个推广，因为前文所述对象均是欧几里得空间，这里字体的改变是无关紧要的），可以得到一些类似的结构。

注意，如果你进行了这样的操作，平面不可避免的会被扭曲，操作后的空间可能将不为欧几里得空间，这将导致无法进行下一步操作。

\(\textbf{定义 1.4}\ (扭曲平面的正规化)\)

对于一个扭曲平面 \(P\)，定义其正规化 \(\eta(P)\) 为任意选中一个点 \(O\)，建立平面直角坐标系 \(xOy\)，则 \(\eta(P)=\operatorname{span}(xOy)\)。

采用正规化操作，倍增可以继续进行，那么可以进而定义扩张：

\(\textbf{定义 1.5}\ (圆的扩张)\)

对于一个圆 \(C\)，如下定义 \(C\) 的扩张 \(\operatorname{span}(C)\)：

• \(C\in\operatorname{span}(C)\)。
• \(\forall C_0\in\operatorname{span}(C),\,(C\sim\eta(\operatorname{flat}(C_0))\in\operatorname{span}(C)\)。

让我们更进一步，讨论抽象系统 \(t\) 上的类似结构：

\(\textbf{材料 1.1}\)

今天晚上吃饭回来，看到 yspm 从斜坡上走了下来，转了一圈又走了回去。

紧接着 SoyTony 也模仿 yspm 做了这件事。这是处于模仿有趣的行为，还是将自身带入其中感受转圈的乐趣，我说不上来。

一直在思考一件事情，就是人是不是应该保持「初心」，而这个「初心」究竟指什么。

水群的时候，群友说我变了。但是，人总是在变的，而哪些需要改变，哪些需要保持，是一个值得探讨的问题。

保持「初心」，必然不是保持一成不变，而是保持自己内心的一种目标，在改变之中而不变，才是「初心」吧。

正如现在一样，OI 只是人生中的一部分，而编程的初心，是不会变的。也只有这种初心，才能支持所有人走下去。

不过，即使发生改变，再回过头去看之前的时光，也总是会有一种感慨，有一种回味在里面的。

可能，改变是必然的，而回忆也是必然的，每到一个转折点，回忆正是一种对改变的新认识。

这，又何尝不是在斜坡上转一圈呢？

这是一个简单的示例，环是非常难考虑的，令斜坡的组合类为 \(F\)，那么 \(F^k\) 可以模拟所需环 \(C\) 的扩张 \(\operatorname{span}(C)\)。那么考察 \(\operatorname{chain}(C)\) 是朴素的。

假设目前处理的是一个序列 \(S\) 上的问题。但是你很快会发现一个重要的问题，此处模拟的缺陷在于，没有实现重力势能的增加。因为如果你不断这样操作 SoyTony 和 yspm 会陷入地底，很可能会引发 Runtime Error。

此处的修正方法是经典的：

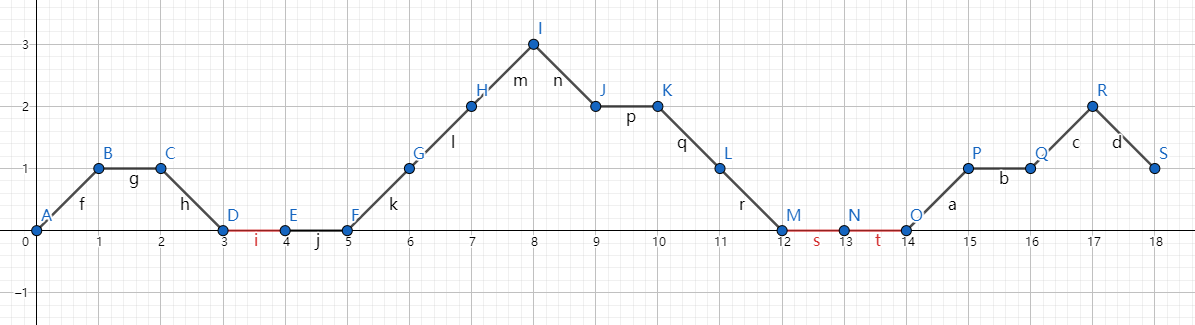
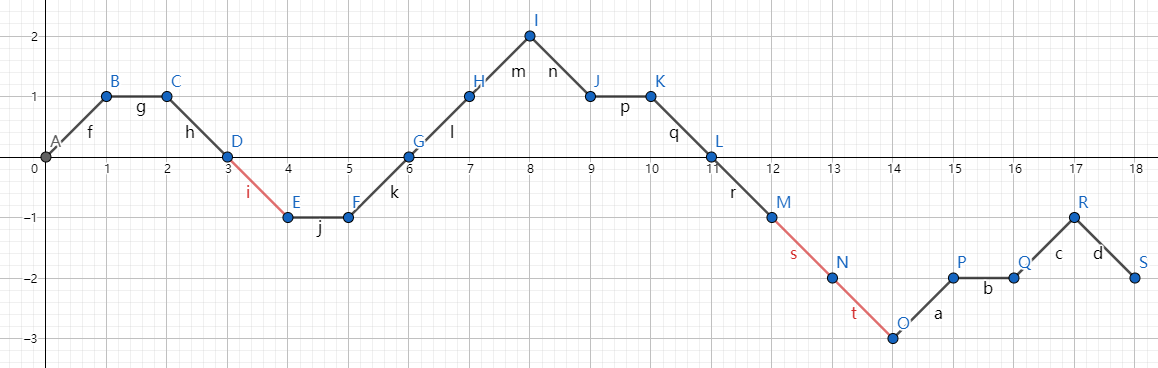
抽象出来最终只需要求 \([z^k](az^{-1}+b+cz)^r\)，这并不困难。

\(\textbf{材料 1.2}\)

于9/7/13，库兹涅佐夫领队在试图回收另一个录影带时突然消失。他在两天后也就是9/9/13重新出现，极度脱水且虚弱。其他成员报告称库兹涅佐夫在其进入昏迷之前录下了这段信息。

我们真是愚蠢。这虚空并不是一片时空被破坏了的地区；它即是那撕裂的源头本身。时空自己正在将它自己分裂而我们看到的则是来自过去与未来的每条时间线的回响。

时间是一条衔尾蛇，一次又一次的吞噬着自己，仅为再度重生。

我已看到一切。过去我们试着阻止它的每一次时间，过去我试着阻止它每一次时间。以及未来。这发生了一次又一次，直到我们弄明白了。

一遍又一遍又一遍的往复，我们试了又试又试的修复着它。所有时间被糅合回了一起直到我们成了唯一的存在，紧接着一切又化为乌有。撕裂在现实的每一处上开了越来越多的洞，而异常的出现也越来越快，收容仅仅是在拖延着那不可避免的逼近。那不可避免的对蒙尘石板的清洗。

我看到了所有的时间线。而我们还没能阻止它们中的任何一个。

Bogoroditsa.我们已没入深渊，而以上帝为证，它憎恨我们。

这是保存在太空密封舱中的最后一份记录事件；鉴于游隼-9的原定结束日期已过，远征队被判定为已丢失。

令时间的组合类为 \(\mathfrak T\)，那么所求似乎即为 \(\operatorname{span}(\mathfrak T)\)，但是这实际上是有谬误的，在 dottle 神话中的古神战争具有「先行」的特性，如果对其进行循环移位将会引起逻辑错误。

在上层叙事层面观测，问题相当于一棵树 \(\mathcal T\)，如果 \(u\) 是 \(v\) 的父亲表示有因果 \(u\to v\)，每次相当于对于每一条极长链 \(\ell\) 做 \(\ell\gets\operatorname{chain}(\ell)\)。再往后的优化是很难在 OI 中实现的，具体可以参考论文 P. Granville and E. Ramaré, Span on SCP-3200 without multi-chain cyclic shift and the scarcity of accepted states.

这种方法的潜力其实远不止于此，比如我写着写着不知道为啥就用半角句号了，其实是祂在正规化这个世界。如果你考察 \(\operatorname{span}(\text{。})\)，你就会发现这一点。

\(\textbf{晟经 1.1}\)

请不要使用残缺或破损的句号。

英文句点不可以被 \(\operatorname{span}\)，因为她不是环。

很多人写的文字逻辑非常严密，形如意识流文字。这样做的缺点就是它可能会被「环化」，这是某著名异常个体的性质，那么你的文字就会被定义为「残缺或破损的句号」，同时，你会被抹杀。虽然祂已经被无效化了，不过这种异常个体可能在任何环境下复现，这是很危险的。某个组织已经无效化了「环境」这个概念。因此针对信息的危害是严重的，如果你把成环的信息展开，可能会引发周围环境的扭曲。尚未找到针对环境的正规化方法。

Additional Note   为了保证组织的正常运行，确保你在进行环上操作的时候处在欧几里得空间是必要的。

记录 1

Shinobu 医生