2023.7.28 闲话
CF1845D Rating System
注意到一个 的影响相当于将一段区间内的贡献全部消除,对于任意一段区间,都可以构造出对应的 使得消的贡献包含对应区间,因为选不满一定不优,所以找最小子段和是正确的 .
时间复杂度 .
CF1843F Omsk Metro
因为点权只有 和 所以对于最大子段和和最小子段和它们中间必然都是可以作为一个子段和的,于是只需要维护最大子段和和最小子段和即可 .
时间复杂度 .
CF1841C Ranom Numbers
大力 DP 虽然可以,但是注意到每个字符只有修改第一个或最后一个可能成为最优答案,暴力修改后模拟即可 .
时间复杂度 ,其中 是字符集大小 .
CF650D Zip-line
会写的 .
CTSC2006 歌唱王国
为什么我要做这个题啊 . 令 表示结束时字符串长度的 PGF, 表示未结束时字符串长度的 PGF,那么答案就是 .
在 后面加一位可以导出 .
两边同时求导可以得到 ,代入 可以得到 .
对于酋长的名字 ,在 后面加一个 可以导出:
注意如果是 border 就选不满了 . 贺一个 gtm1514 贺过的图:
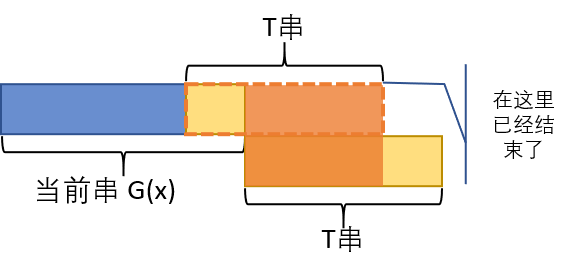
那么代入 后可以得到:
直接做就行了,时间复杂度 .
以下是博客签名,正文无关
本文来自博客园,作者:yspm,转载请注明原文链接:https://www.cnblogs.com/CDOI-24374/p/17521374.html
版权声明:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议(CC BY-NC-SA 4.0)进行许可。看完如果觉得有用请点个赞吧 QwQ



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】
2022-07-28 魔怔愉悦之 Vizing 定理