2023.6.5 闲话

隔壁 K8He 大肆宣传他优异的 whk 成绩，然而我物理甚至不及格 TAT（
UPD. 自我批评 .

原来那个宏定义双向 FOR 有点缺陷，以下是改进版：

#define FOR(i, a, b) for (int _L=a,_R=b,_D=(0<_R-_L)-(_R-_L<0),i=_L; i*_D<=_R*_D; i+=_D)

推一下 STAOI G - Round 2（虽然好像没有什么明确理由推这个）.

翻到一个 2022-04-23 整的东西，好像还挺有意义的（HTML 转义）：¿ == ¿ .

K8He 在被两个人依次推荐 AGC 后真的去做 AGC，真的非常恐怖。希望以后如果 K8He 要推题的话多多推荐 wtf19 .

K8He：化学奥赛不会用百度 .

推歌：イナくなっちゃえ大作戦 / みつあくま feat. 初音ミク .

推歌：To the Milky Way（怨念）

---

以下所有图都是官方题解的 .

目录

• AGC001A BBQ Easy
• AGC001B Mysterious Light
• AGC001C Shorten Diameter
• AGC001D Arrays and Palindrome
• AGC001E BBQ Hard
• AGC001F Wide Swap

AGC001A BBQ Easy

gtm1514 大神曾经说过，入门也要做难题也要做才健全……

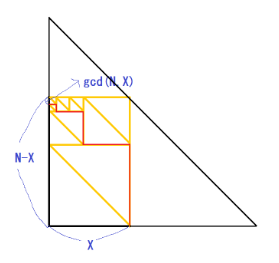
AGC001B Mysterious Light

\(3 (A - \gcd(A, B))\) Problem .

AGC001C Shorten Diameter

枚举最中间的点或者边，然后搜就行了 .

AGC001D Arrays and Palindrome

一种基本想法是对于一个 \(a\) 序列覆盖的区间 \([l,r]\) ，构造 \(b\) 序列覆盖 \([l,r-1]\)，那么不难发现 \([l,r]\) 必然全部相等 .

如此构造，则每个 \(a\) 覆盖的区间都对应相等，那么接下来只需要构造使得每个区间也相等即可，只需要让 \(b\) 序列的区间伸长到随便一个相邻的 \(a\) 管辖的位置即可，很自然的想法就是让它覆盖 \([l-1,r-1]\)，边界情况特殊处理一下就好了 .

不过这样只有 \(a\) 覆盖的区间长为偶数是对的，具体可以考虑对于偶数情况可以去掉首尾字符后变成原来的模式，而奇数所构建出的则是两个置换环的位置对应相等（也就是奇数位、偶数位对应相等）.

不过边界情况还是要特殊考虑，可以发现长度为奇数的段在开头和末尾时按如上构造是可以满足条件的 .

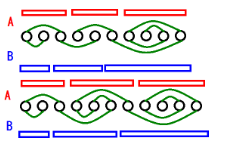
那么只需要把 \(a\) 中的奇数放到头尾就可以了，但是这样无法处理奇数段个数大于 2 的情况 . 其实，可以证明，这种情况一定是无解的 . 以下来自官方题解 .

假设 \(a\) 中有 \(O_a\) 个奇数段，\(b\) 中有 \(O_b\) 个奇数段，那么可以构建出的等价关系就是 \(\dfrac{n-O_a}{2}+\dfrac{n-O_b}2\) 个，而 \(n\) 个点需要全部等价至少需要 \(n-1\) 条边，则导出 \(\dfrac{n-O_a}2+\dfrac{n-O_b}2\ge n-1\)，于是不难得到 \(O_a+O_b\le 2\)，所以有多于 2 个奇数段的情况肯定是无解的 .

这样，所有情况已经考虑完毕，模拟即可 . 注意对于长度为 1 的区间和 \(m=1\) 的特殊处理 . 时间复杂度 \(\Theta(m)\) .

AGC001E BBQ Hard

经典，看组合意义就是格路计数，起点是 \((-a_i,-b_i)\) 终点是 \((a_j,b_j)\) .

那么用类似 Common（来自学长的馈赠 1）的 Trick，统一算所有起点的贡献，DP 处理即可 .

时间复杂度 \(\Theta(n+V^2)\) 其中 \(V\) 是值域 .

AGC001F Wide Swap

对于给出排列 \(p\)，将其看做置换，则可以求出其逆 \(\pi=p^{-1}\) .

那么操作的形式就变成了交换相邻的差值不小于 \(k\) 的数，字典序的限制也就是要求 \(\pi\) 中值小的尽量靠前 .

考虑归并，记一下前缀最小值就能合并了 . 时间复杂度 \(\Theta(n\log n)\) .

做法详细正确性证明可以看洛谷讨论区，我就不再复读一遍了 .