2023.6.1 闲话

儿童节，好耶！

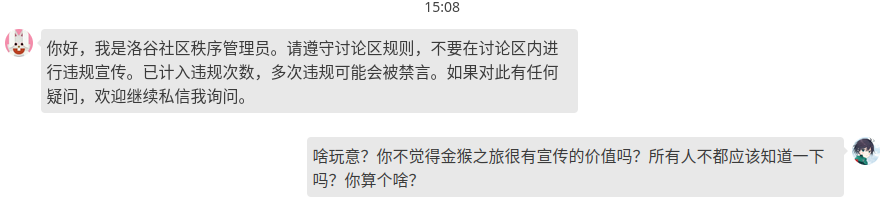
推歌：おもちゃの変異体 / サカダケイ feat. 歌愛ユキ .

推歌：Dialnote（绝世好歌）

ABC298Ex Sum of Min of Length

考虑每个点离 \(L_i\) 和 \(R_i\) 距离大小关系变化的分界位置：

• 如果 \(d(L_i,R_i)\) 是偶数，那么分界就是链 \(L_i-R_i\) 的中点 \(M\)，可以拆出来：
  \[\min\{d(L_i,x),d(R_i,x)\}=d(i,L_i)+d(i,R_i)-d(i,M)-\dfrac12d(L_i,R_i) \]

• 如果 \(d(L_i,R_i)\) 是奇数，此时分界在一条边上，令边的那个深度较大的邻接点为 \(M\)，那么考虑邻接点偏移到 \(M\) 总共产生了 \(\dfrac n2-\operatorname{size}(M)\) 的贡献，于是按前一种情况的方法算完之后加上 \(\dfrac n2-\operatorname{size}(M)\) 即可 .

发现最后都是拆成了 \(d(i,u)\) 其中 \(u\) 是定点的形式，那么换根预处理 \(\displaystyle f(u)=\sum_{i=1}^nd(u,i)\) 即可 .

时间复杂度 \(\Theta((n+q)\log n)\)，实现的好的话可以不带 log（不带 log 离线的比较好做，在线比较麻烦）.

ABC301F Anti-DDoS

可以发现一个串合法当且仅当最后一个后面有大写字母的小写字母左边没有两个相同大写字母 .

那么枚举这个小写字母，只需要计算：

• 对于一个前缀，没有两个相同大写字母的方案数 .
• 对于一个后缀，其开头作为最后一个后面有大写字母的方案数 .

第一个问题是平凡的，对于一个有 \(n\) 种大写字母和 \(m\) 个 ? 的串，可以通过枚举大写字母的数量来求得方案数：

\[\sum_{i=1}^{\min\{m,26-n\}}26^{m-i}\binom mi\binom{26-n}ii! \]

第二个问题考虑一个 DP，令 \(dp_{i,0/1}\) 表示 \(i\dots n\) 其中 \(i\) 是/不是大写字母且 \(i\) 是最后一个后面有大写字母的小写字母的方案数，转移平凡 .

这样的话枚举之后两部分答案乘起来求和即可，需要特殊处理整个序列只有大/小写字母或者所有小写字母都在大写字母后面的情况，方案数是 \(dp_{1,0}+dp_{1,1}\) .

时间复杂度 \(O(Sn)\) 其中 \(S=26\) 是我原神 uid 末两位 .

ABC302F Merge Set

就是相当于要对所有相交的集合连边权为 1 的无向边，考虑优化建图 .

对于集合 \(S\) 和元素 \(x\in S\)，连边 \(S\xrightarrow{0}x,\,x\xrightarrow{1}S\)，然后跑 01BFS 即可 .

时间复杂度 \(\Theta(n+m)\) .

ABC302G Sort from 1 to 4

按 \(1,2,3,4\) 的个数分成四段，那么令 \(a_{i,j}\) 表示第 \(i\) 段中 \(j\) 的数量，那么就是要让所有 \(i\neq j\) 的 \(a_{i,j}=0\) . 每次可以选在 \(i,j\) 段的 \(x,y\) 然后让 \(a_{i,x},a_{j,x}\) 加一，\(a_{i,y},a_{j,y}\) 减一 .

按行考虑可以发现肯定是先把 \((i,j),\,(j,i)\) 这种改成 \((i,i),(j,j)\)，模拟就可以了 .

时间复杂度 \(\Theta(n)\) .

ABC302Ex Ball Collector

首先考虑怎么做 \(v\) 一定的，对于每个 \((a_i,b_i)\) 连边，那么对于一个连通块来说，答案就是点数和边数的 min . 那么只需要求出所有连通块的点数边数 min 之和即可，并查集动态维护点数和边数就好了 .

如果 \(v\) 变的话考虑在树上 DFS，那么只需要处理加入一个点和删除一个点的贡献，把并查集改成可撤销并查集即可 .

时间复杂度 \(O(n\log n)\) .

ABC303G Bags Game

三次方复杂度的区间 DP 大家都会，就不说了 .

发现区间长度肯定是越转移越小，于是按区间长度从小到大处理，每次转移就是区间 max，ST 表即可 .

时间复杂度 \(\Theta(n^2\log n)\) .

---

image from wkh2008

png 也能动，好像是直接改扩展名的 trick？