
推歌:世界は可愛く出来ている
东方兽王园的灵梦新曲,还挺可爱的 .
看 PinkRabbit 数论课件有这个建立递归关系的 Trick(什么,你的课件都是从小学数学讲到 NOI 的吗).
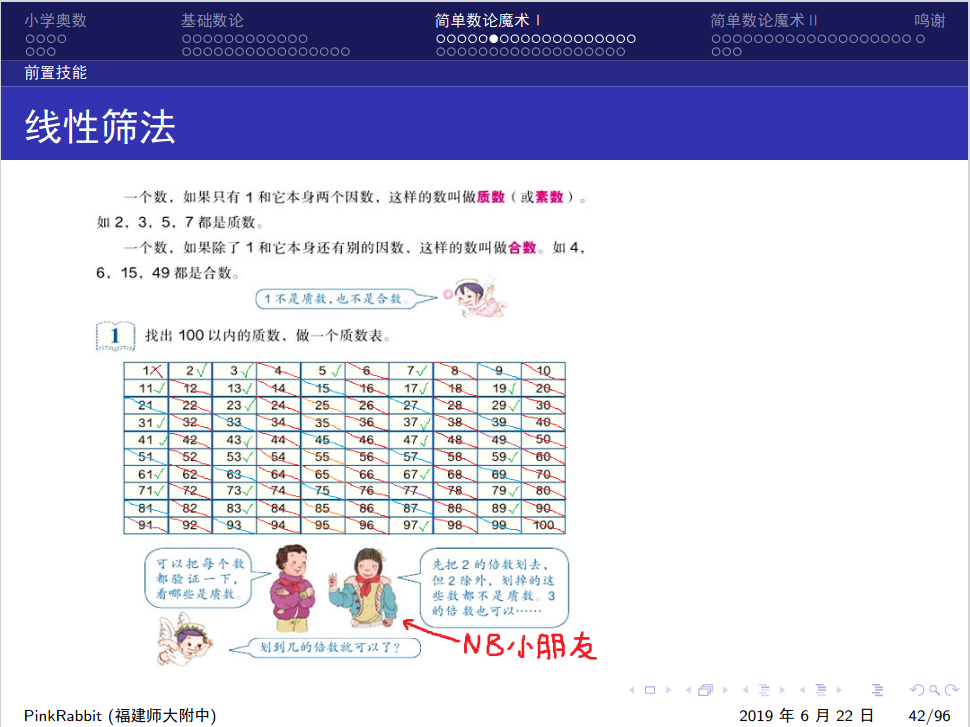
问题:计算 n∑i=1μ(i)[i⊥k] .
令 F(n,k)=n∑i=1μ(i)[i⊥k],则可以建立递归关系:
F(n,k)=n∑i=1[i⊥k]μ(i)=n∑i=1μ(i)∑d∣gcd(i,k)μ(d)=∑d∣kμ(d)⌊nd⌋∑i=1μ(id)=∑d∣kμ(d)⌊nd⌋∑i=1μ(i)μ(d)[i⊥d]=∑d∣kμ(d)2F(⌊nd⌋,d)
那么递归即可 . 有用的 d 肯定是 square-free 的,那么只有 2ω(d) 种 .
可以看成 DAG 上 1→n 所有路径点权积之和,而只有 1 的点权和 n 有关 . 所以如果 k 不变的话,可以处理出 F(k,k) 之后 Θ(1) 得到别的位置的答案 .
推广路线 1:使用完全一致的推导过程,不过 μ 改成了 φ(其中 φ−1 是 1φ(x),不是 Dirichlet 卷积逆):
F(n,k)=n∑i=1φ(i)gcd(i,k)φ(gcd(i,k))=n∑i=1φ(i)∑d∣gcd(i,k)(φ−1∗μ)(d)=∑d∣k(φ−1∗μ)(d)⌊nd⌋∑i=1φ(di)=∑d∣kφ(d)(φ−1∗μ)(d)⌊nd⌋∑i=1φ(i)gcd(i,d)φ(gcd(i,d))=∑d∣kφ(d)(φ−1∗μ)(d)F(⌊nd⌋,d)
推广路线 2:改成二维的:
F(n,m,k)=n∑i=1m∑j=1[i⊥j][j⊥k]=n∑i=1[i⊥j]m∑j=1∑d∣gcd(j,k)μ(d)=n∑i=1∑d∣kμ(d)⌊md⌋∑j=1[i⊥jd]=∑d∣kμ(d)n∑i=1⌊md⌋∑j=1[i⊥j][i⊥d]=∑d∣kμ(d)F(⌊md⌋,n,d)
(感觉这个推导非常科幻……怎么想出来这么厉害的东西的)
应用:NOI2016 循环之美(其实就是推广路线 2).
题解(大众解法)
假设 n,m 同阶 .
额首先既约既约分数 xy 在 k 进制下纯循环当且仅当 y⊥k .
因为如果循环节长度是 c 那么肯定有 x≡x⋅kc(mody),又因为 x⊥y 那么就是 kc≡1(mody),所以只有 y⊥k 的时候才有满足条件的 c,这样就证明了结论 .
于是答案就是 n∑i=1m∑j=1[i⊥j][j⊥k],化简一下:
n∑i=1m∑j=1[i⊥j][j⊥k]=m∑i=1[i⊥k]n∑j=1[i⊥j]=min{n,m}∑d=1[d⊥k]μ(d)⌊nd⌋∑i=1⌊md⌋∑i=1[j⊥k]=min{n,m}∑d=1[d⊥k]μ(d)⌊nd⌋⌊md⌋∑j=1[j⊥k]
那么整除分块后就是要求:
f(n,k)=n∑i=1[i⊥k]g(n,k)=n∑i=1[i⊥k]μ(i)
分别看一下:
f(n,k)=n∑i=1[i⊥k]=n∑i=1[imodk⊥k]=⌊nk⌋f(k,k)+f(nmodk,k)g(n,k)=n∑i=1[i⊥k]μ(i)=n∑i=1μ(i)∑d∣gcd(i,k)μ(d)=∑d∣kμ(d)⌊nd⌋∑i=1μ(id)=∑d∣kμ(d)⌊nd⌋∑i=1μ(i)μ(d)[i⊥d]=∑d∣kμ(d)2g(⌊nd⌋,d)
这样对于 f 来说因为 k≤2000 所以预处理出小的 f 之后就能算了 .
对于 g 来说暴力记忆化递归算,因为外层有整除分块所以复杂度不太好分析 . 毛估估一下的话如果光看递归树大小涉及到的不同状态的数量是 O(ω(k)√n) 级别的,底层 k=1 的块筛部分用杜教筛的话时间复杂度就是 O(n2/3) . 那么可以得到一个时间复杂度的上界是 O(ω(k)logn+n2/3) .
那么整合一下的话时间复杂度就是 O(k+n2/3+ω(k)logn),可以通过 .
(我写的没有那么精细,算 g 是 O(n2/3+√klogn) 的也过了)
感觉也不是很麻烦为什么最后渲染出来这么长





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】