2023.5.26 闲话

Typical DP Contest，可以看看 .

正文里都用不了 JS 吗，我申请权限了啊（我记得 DeepinC 能用来着，，）

整了一个双向都能用的宏定义 for，感觉有点趣味：

#define FOR(i, a, b) for (int i=a, d##i=(a==b)?1:(b-a)/abs(a-b); i*d##i<=b*d##i; i+=d##i)

\(\Huge{\tt vim+经常保存+敲键盘响=？}\)

---

shaber W|A

Input: prove by induction sum of j from 1 to n = n(n+1)/(2.0000000000000000001) for n>0

---

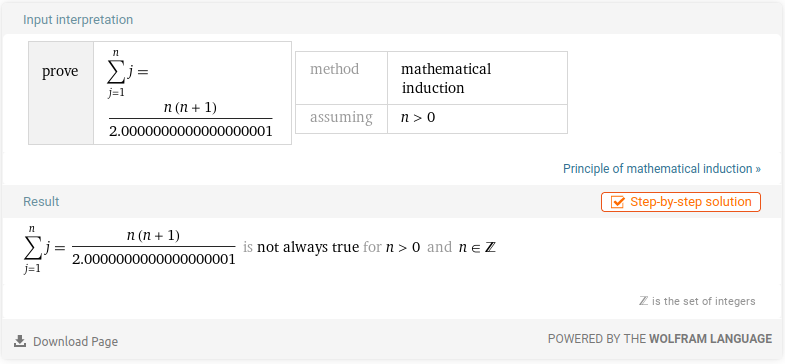
Karin 的弹幕

维护一个序列 \(\{a_n\}\)，\(q\) 次询问，支持：

• 单点修改 .
• 求对一段下标是等差数列的子序列的最大值 .

\(1\le n,q\le 7\times10^4\)，10s .

还行吧，等差数列其实就相当于模公差是定值，可以想根号分治 .

于是就令阈值是 \(B\)，大于 \(B\) 的公差暴力，小于等于 \(B\) 的公差对于每个公差线段树维护即可 .

时间复杂度 \(\Theta(n+nq/B+(nB+q)\log n)\)，设 \(n,q\) 同阶，则取 \(B=\sqrt{n\log n}\) 得最优时间复杂度 \(\Theta(n\sqrt{n\log n})\)，10s 还是能过的 .

ABC300E Dice Product 3

答案满足 \(f(n)=\dfrac{\sum\limits_{k=1}^6f(\lfloor n/k\rfloor)}6\) .

那么移项之后记忆化搜索即可，至少能分析到 3 个 log .

ABC300G P-smooth number

膜拜 liqingyang 大神 . 暴搜，递归到 \(k=2\) 处特判跳出，对于 \(n\) 较小的部分记忆化，因为状态数并不是很多就过了 .

（其实可以看样例那个极限数据答案才 2345134674）

标算是 meet-in-the-middle，把素因子分成 \(2,3,5,7,11,13\) 和其它，处理出仅含小素因子的序列 \(v_1\) 和仅含大素因子的序列 \(v_2\) .

特判 \(p\le 13\) 的情况 . 然后考虑满足条件的 \(x=pq\le n\) 其中 \(p,q\) 是在 \(v_1,v_2\) 里分别选的，那么枚举 \(p\) 后在 \(v_2\) 里二分 \(q\) 的范围就行了 .

极限情况 \(v_1,v_2\) 的长度分别是 511985 和 8860016，还可以接受 .