2023.4.26 闲话

蚌：

---

ABC299G Minimum Permutation

给值在 $[1,m]$ 的序列 $\{a_n\}$，找到一个长度为 $m$ 的字典序最小的子序列，且满足其是一个排列 .

$1\le m\le n\le 2\times 10^5$ .

考虑从前往后贪心选，根据一些观察可以知道如果三个位置 $i,j,k$ 满足 $a_i<a_j$ 且 $a_i=a_k$ 那么选 $a_i$ 一定不优，于是预处理每个数最后一次出现的位置后 单调栈维护即可 .

时间复杂度 $\Theta(n)$ .

ABC293F Zero or One

给正整数 $n$，问有多少个正整数 $b$ 使得 $b$ 进制下 $n$ 只含 0 和 1 .

最多 $1000$ 组询问，$2\le n\le 10^{18}$ .

¿

考虑阈值分治，设阈值 $B$，则对于 $b\le B$，暴力枚举每个 $b$ 后分解判断，对于 $b>B$，枚举每种 $b$ 进制下仅含 0 和 1 的数后二分出是否存在 $b$ .

那么时间复杂度就是单次 $\Theta(B\log n+2^{\log_B n}\log n\log_B n)$

这个平衡好像不太可能初等完成，不过取 $B=\Theta(2^{\sqrt{\log n}})$ 可以得到单次 $\Theta(2^{\sqrt{\log n}}(\log n)^{1.5})$ 的时间复杂度下界，实际我取的 $B=2\times 10^3$（是不是差有点大） .

有一种无脑做法：注意到 $b$ 肯定是 $n$ 或 $n-1$ 的因子，Pollard-Rho 分解后暴力判断即可 .

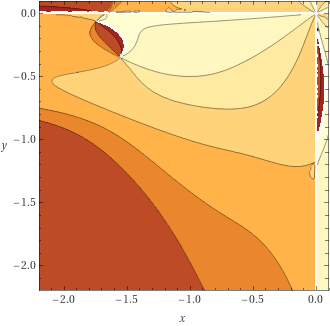
ABC292F Regular Triangle Inside a Rectangle

问 $a\times b$ 矩形里最大能放边长多大的等腰三角形 .

$1\le a,b\le 10^3$ .

弃疗 .

不难发现肯定是 $a,b$ 相差比较远就直接平放，否则固定一个端点另两个在边上 .

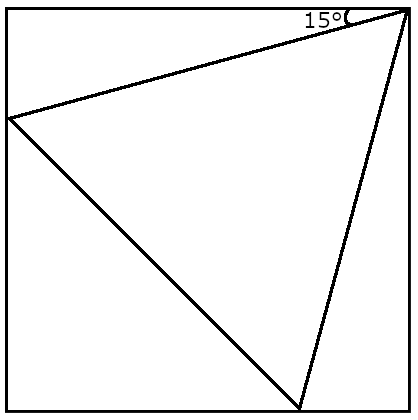
如图是 $1\times 1$ 的情况（固定一个端点另两个在边上）.

不失一般性让 $a\le b$，那么 $a\le \dfrac{2\sqrt3}3b$ 时比较显然答案就是 $2\sqrt{b^2-\sqrt 3ab+a^2}$ .

否则 $a=b$ 时答案是 $a$，$a=\dfrac{2\sqrt3}3b$ 时答案是 $\dfrac{2\sqrt 3}3b$，这两个都平凡，根据数学直觉可以猜想答案是线性的，于是答案的表达式就可以得到了：

$$ans=\begin{cases}2\sqrt{b^2-\sqrt 3ab+a^2}&a\le\dfrac{2\sqrt3}3b\\\dfrac{2\sqrt 3}3a&a>\dfrac{2\sqrt3}3b\end{cases}$$

理性分析一下好像还是比较容易，因为不想配图所以就不写了 .

SCOI2009 游戏

对于所有 $1\dots n$ 的排列，问其所有置换环大小的 LCM 有多少种不同取值 .

$1\le n\le 1000$ .

发现排列并没有什么用，实际上置换环大小可以等价的转化为任意一组 $n$ 的拆分 .

然后再观察发现只有 square-free 的数有贡献，别的可以丢掉不看，然后整一个 $\Theta(n^2)$ 的 01 背包就完了 .

HNOI/AHOI2018 道路

给一个二叉树 $\mathcal T$，每个非叶子节点可以标记到左儿子的边或者到右儿子的边其一 .

每种情况的代价为

$$\sum_{i=1}^nc_i(a_i+x_i)(b_i+y_i)$$

其中 $a,b,c$ 给定，$x_i,y_i$ 分别为 $i$ 到根路径上未被标记的左儿子边 / 右儿子边个数 .

问最小代价是多少 .

$1\le n\le 2\times 10^4$，$1\le a_i,b_i\le 60$，树深度不大于 $40$ .

朴素 DP，令 $dp_{u,l,r}$ 表示 $u$ 到根有 $l$ 个未被标记的左儿子边，$r$ 个未被标记的右儿子边，转移平凡 .

需要根据树深度的限制卡一卡空间 .

时间复杂度 $\Theta(nV^2)$ .