2023.6.12 闲话
很多人不知道现在已经是 6.12 了,其实我生活在美国(不是地球上那个,但是同构),在机房只不过是我的投影。
推歌:
- 鏡の魔法 - ひとしずく×やま△ feat. 镜音レン .
- 魔法の鏡 - ひとしずく×やま△ feat. 鏡音リン & 鏡音レン .
这个其实我更偏好鏡の魔法一点,魔法の鏡就感觉旋律比较平淡了 . 一滴P 确实是很强大的,比如 Mr.シャーデンフロイデ、祝福のメシアとアイの塔和背徳の花都是非常优秀的曲目 .
推歌:Defection - TeddyLoidfeat feat. DELTA .
因为我 cnblogs 99 粉丝了,并且 joke3579 洛谷给我发私信了,非常愉悦,所以放了个这个 .
大概就是基于 Richard P. Stanley 的 Enumerative Combinatorics Volume 2 和 Catalan Addendum,不过只写了前面几个题(烂尾). Catalan 数的这类问题一般被称作 Catalania (Catalania = Catalan mania) 好像 .
我要是以后有空可能会补一下没看的题目,不过可能到 AFO 了也没空 .

不一定能完全领悟到原作者的意思,可能有的地方有问题 /kk
前置知识
基本定义
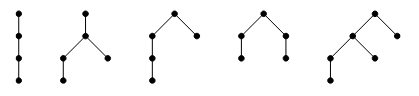
平面树 (plane tree):
- 有根:就是儿子顺序区分的树之类的,后文平面树一般都是有根的 .
- 无根:儿子顺序循环同构之类的 .
内部点 (internal vertix/node) 就是非叶子节点 . trivalent 树就是每个点度为 0 或 2 的树 .
OI 中好像不太用这种词,别不知道是啥了 .
可能和别的地方的定义不太一样,这个问题不大 .
文中右链默认极长 .
关于 Catalan 数
Catalan 数 满足以下等式:
Catalan 数 OGF 的封闭形式:
同时,有 .
另外,记
分别表示 Catalan 数偶数位和奇数位的 OGF .
常见问题:

(Enumerative Combinatorics Volume 2, Page 173)
这张图里有本文涉及的 Dyck 路和 ballot sequence 的定义,可能和别的地方不太一样,注意一下 .
正文
只写 6.19 章的可做非平凡题目 .
Exercises
计数 个点的平面树,满足每个满足儿子数量和父亲的儿子数量的最小值大于 1 的点的右链的长度都为偶数 .
用常见的构造 Dyck 路到平面树双射的方法即可变成问题 ,也就是下一个问题 .
(原文是 Plane trees with vertices such that the rightmost path of each subtree of the root has even length,疑惑)
计数长为 的 Dyck 路,满足每个 的极长连续段的长度为奇数 .
令 分别是长为 ,只在开头和结尾碰 轴,且每个 的极长连续段的长度为奇数 / 偶数的 OGF .
那么不难发现的是 且 . 由此解得 .
那么答案的 OGF 就是 ,很好 .
计数长为 的 Dyck 路,满足没有高为 2 的峰(一个峰定义为连续的步 和 夹住的点).
构造双射,首先在路径前添加一个 ,然后给所有没有高为 1 的峰的极长 Dyck 路抬高一层,最后删掉所有形如 的子 Dyck 路 .

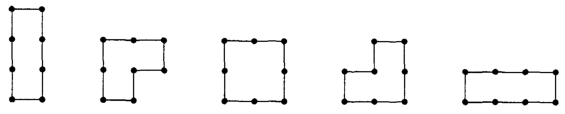
计数两条长为 的路径,其中只使用 步且只在开头和结尾处相交 . 如果两种方案看起来一样那么它们就一样 .
注:这种图案被称作 parallelogram polyomino .
直接考虑图案,令 表示第 行的方格数, 表示第 列的方格数,构造序列 :
次幂表示重复若干次 .
那么可以发现构造出了原问题到 ballot sequence 的双射 . 这样就做完了 .
计数两条长为 的路径,其中只使用 且在开头和结尾处相交,满足有一条路径永远不必另一条高 . 如果两种方案看起来一样那么它们就一样 .
去掉 中两条路径的开头和结尾步即变成这个问题 .
计数 个圆周上的点间连 条不相交弦的方案数 .
钦定一个点出发顺时针走,遇到一条弦的时候第一次走 ,第二次走 ,那么与 Dyck 路形成双射 .
计数 个有序点间连 条不相交弧的方案数,弧的方向只能向上 .
把 破环为链 .
计数 个有序点间连 条不相交弧的方案数,弧的方向只能向上,弧之间构成一棵树且弧两两不交 .
注:问题中的树被称作 noncrossing alternating tree .
注意到总有一条边从最左边的点连向最右边的点,考虑删掉这条边,那么问题可以被分为两个子问题,这导出了与 Catalan 数相同的递推式 .
计数对于任意 满足 的不减正整数序列 .
考虑从 走到 且不经过对角线的格路计数问题,考虑每个 步下方的面积即可构造出两者之间的双射 .
计数对于任意 满足 的递增正整数序列 .
使用常见手法去掉递增的严格:给 减 即变成问题 .
计数满足 且 的整数序列 .
考虑把第 位改成一个 后面接 个 ()即构造出与 ballot sequence 的双射 .
计数满足 且 的所有前缀和非负的整数序列 .
虽然和 是一样的,但是看起来好像也没那么平凡 . 和 就差一个首项,把首项也参与差分即可 .
Addendum
计数满足如下条件的有 个内部点的平面树的个数:
- 每个内部点的儿子数量为 1 或 2 .
- 儿子数量为 1 的点只在从根出发的右链上 .
按照 DFS 序遍历树,往左儿子走或者唯一的一个儿子走的时候走 U,否则走 D,那么就建立起这个和 Dyck 路的双射,关于构造与 Dyck 路的双射的一些说明见 2023.4.9 闲话 .
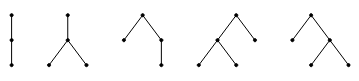
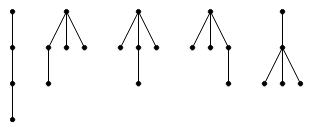
计数 个点的平面树,其中从左到右遍历根的每个子树先有大小是偶数的子树再有大小是奇数的子树 . 并且大小是偶数的子树被染上红色或蓝色 .
写出答案的 OGF 就是 .
那么根据一些玄学操作就可以得到 OGF 其实就是 .
好像是 L. Shapiro 的结果,具体证明过程我还不太清楚 .
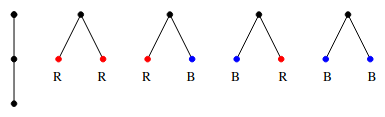
计数 个点的平面树,叶子被染成红色或蓝色 .
还是考虑构造与 Dyck 路的双射,开局走一个 U,按欧拉序遍历,如果往下走就 U,往上走就 D,不过蓝色叶子的位置走 UD,结尾走一个 D 结束 .
因为开局向上平移一位所以 UD 一定合法,又有红色叶子走 DU,这样就把红色叶子和蓝色叶子区分开了 . 这是相较于任意平面树的改进之处 .
计数有 个内部点的平面树,满足每个有两个儿子的结点的左儿子一定是内部点 .
按 DFS 序走,对于一条边 ,其中 离根较远 . 如果 没有兄弟,则如果 是左儿子,把它则走 U,如果是右儿子则走 D . 这样就和 Dyck 路双射了 . 其实就是和 差不多的方法 .
计数满足以下条件的平面树:
- 每个结点的儿子数量为 0, 1, 3 中的一个 .
- 有 个结点有 0 或 1 个儿子 .
构造双射:把二叉树分成左子树,右儿子的左子树和右儿子的右子树 .
或者写出答案的 OGF 满足 . 那么可以解得 .
计数 个点的无根平面树,其中每个点被染成红蓝两色(相邻结点不同色),且以一条边为根 .
考虑建立圆上不相交弦问题(即 )和此问题的双射 . 如下图构建一棵树 ,即原图的「内部对偶图」:
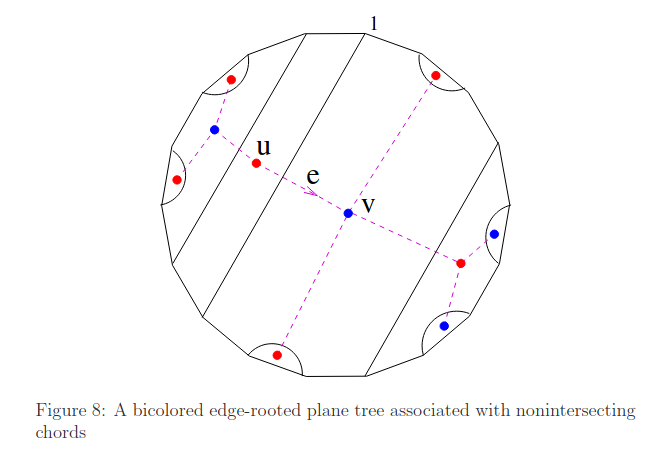
那么如果有 条弦,则 显然是 个点的无根平面树,让根边为与包含顶点 的弦相交的边,即图中 .
那么交替给每个点染色即可,这样就构建出了圆上不相交弦问题和此问题的双射 .
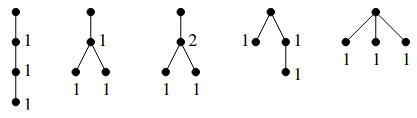
计数 个结点的平面树,每个非根结点有正整数点权,且满足如下条件:
- 叶子的点权为 .
- 对于任意不是叶子或根的结点,其点权不大于其儿子的点权和 .
- 深度最大的点在从根出发的右链上 .
首先删掉所有叶子的点权,然后将每个点的点权放到其到父亲的边上 . 从下往上处理每一条边,如果其点权为 ,则将其右边第 个节点移到父亲的最右子树上,然后删掉点权 . 这样就构造出了原问题与任意平面树的双射 .
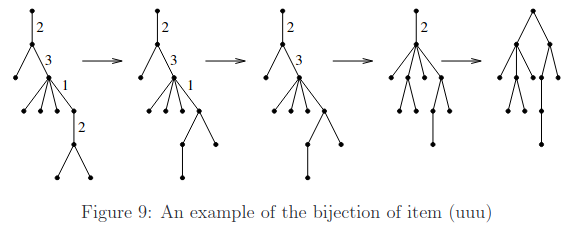
(注:满足前两条的树被称作 树)
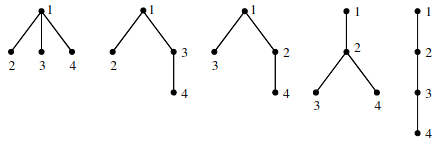
计数 个点的递增平面树 . 叶子节点编号从左到右依次递增 . 且 到 的路径包含所有内部点 .
令 ,则构建出与 的双射 .
计数 个点的有根树,每个内部点有左儿子,右儿子或者中儿子,如果有中儿子则不能有其它儿子,而且每个左儿子必须有非中儿子的儿子 .
论文链接:S. Forcey, M. Kafashan, M. Maleki and M. Strayer, Recursive bijections for Catalan objects, arXiv preprint .
论文建立了 , 和 AHOI2012 树屋阶梯 之间的双射 . 因为太长了就不展开在这里写了 .

以下是博客签名,正文无关
本文来自博客园,作者:yspm,转载请注明原文链接:https://www.cnblogs.com/CDOI-24374/p/17300507.html
版权声明:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议(CC BY-NC-SA 4.0)进行许可。看完如果觉得有用请点个赞吧 QwQ





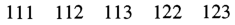
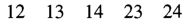



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】
2022-06-11 由竞赛图的分数序列构造出竞赛图