Segment Tree Beats! 初步和其他

不会渐进表示，全无脑用 $\Theta$ 了 /kk

区间最值问题
- 不含区间加减的情况
- 划分数域
历史最值问题

区间最值问题

不含区间加减的情况

Gorgeous Sequence

维护序列 $\{a_n\}$ ， $q$ 次操作：

0 l r v，对于所有 $i\in[l,r]$ 令 $a_i\gets\min\{a_i,v\}$ .

1 l r，求 $\max_{i\in[l,r]}\{a_i\}$ .

2 l r，求 $\sum_{i=l}^ra_i$ .

线段树每个结点上维护和 $s$ ，最大值 $mx$ ，最大值出现次数 $c$ ，严格次大值 $se$ 和区间 checkmin 的标记 .

每次 checkmin 走到结点 $u$ 时：

若 $mx\le k$ ，直接退出 .
若 $se<k<mx$ ，直接修改所有 $mx$ 并打上标记（这里 checkmin 标记和 cover 标记效果一致）.
若 $k\le se$ ，递归进入子结点 .

关于复杂度分析，是关于「标记回收」的系列理论，具体的，称每个节点的最大值为「标记」，并且删去标记值与其父亲结点相同的标记 .

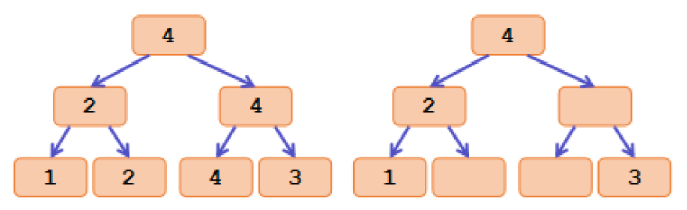
这样线段树中最多有 $n$ 个标记，且每个标记的值都大于其子树中标记的最大值（后者实际上就是严格次大值） . 这样每一个位置实际的值就相当于从它对应位置的叶子出发向上走遇到的第一个标记的值 .

定义标记类满足：

同一次 checkmin 操作产生的标记属于同一类 .
同一类标记下传产生的标记属于同一类 .
否则属于不同类 .

接下来定义每一个标记类的权值等于这一类标记和线段树根节点形成的虚树大小 . 令势能函数 $\Phi(x)$ 为线段树中所有标记类的权值和 .

那么依次分析操作对势能的影响：

对于一次 checkmin 操作，只会增加一个标记类，权值等于打标记时经过的点数，这显然是 $\Theta(\log n)$ .
对于一次标记下传，只让对于类标记的权值增加 $\Theta(1)$ .
考虑暴力递归子节点的过程，这意味着 $v\le se$ 即每到一个节点至少回收一个标记，那么势能减少 $1$ .

这样 $\Phi(x)$ 的总变化量就是 $\Theta(q\log n)$ .

经过以上分析，加上初始的势能，可以得到算法的时间复杂度为 $\Theta((n+q)\log n)$ .

Gorgeous Sequence

比较卡常，要用超级快读才能过 .

struct SegmentTree
{
#define mid ((l + r) >> 1)
#define ls (u << 1)
#define rs (u << 1 | 1)
	struct Node{int l, r, se, mx, cc, tag; ll s;}tr[N << 2];
	inline void pushup(int u)
	{
		tr[u].s = tr[ls].s + tr[rs].s;
		if (tr[ls].mx == tr[rs].mx){tr[u].mx = tr[ls].mx; tr[u].cc = tr[ls].cc + tr[rs].cc; tr[u].se = max(tr[ls].se, tr[rs].se);}
		else if (tr[ls].mx > tr[rs].mx){tr[u].mx = tr[ls].mx; tr[u].cc = tr[ls].cc; tr[u].se = max(tr[ls].se, tr[rs].mx);}
		else {tr[u].mx = tr[rs].mx; tr[u].cc = tr[rs].cc; tr[u].se = max(tr[ls].mx, tr[rs].se);}
	}
	inline void pushdown(int u)
	{
		if (!~tr[u].tag) return ;
		if (tr[ls].mx > tr[u].tag){tr[ls].s -= 1ll * tr[ls].cc * (tr[ls].mx - tr[u].tag); tr[ls].mx = tr[ls].tag = tr[u].tag;}
		if (tr[rs].mx > tr[u].tag){tr[rs].s -= 1ll * tr[rs].cc * (tr[rs].mx - tr[u].tag); tr[rs].mx = tr[rs].tag = tr[u].tag;}
		tr[u].tag = -1;
	}
	void build(int u, int l, int r)
	{
		tr[u].l = l; tr[u].r = r; tr[u].tag = -1;
		if (l == r){tr[u].s = tr[u].mx = a[l]; tr[u].cc = 1; tr[u].se = -1; return ;}
		build(ls, l, mid); build(rs, mid+1, r);
		pushup(u);
	}
	void checkmin(int u, int L, int R, int v)
	{
		if (tr[u].mx <= v) return ;
		int l = tr[u].l, r = tr[u].r;
		if (inrange(l, r, L, R) && (tr[u].se < v)){tr[u].s -= 1ll * tr[u].cc * (tr[u].mx - v); tr[u].mx = tr[u].tag = v; return ;}
		pushdown(u);
		if (L <= mid) checkmin(ls, L, R, v);
		if (R > mid) checkmin(rs, L, R, v);
		pushup(u);
	}
	pair<ll, int> query(int u, int L, int R)
	{
		int l = tr[u].l, r = tr[u].r;
		if (inrange(l, r, L, R)) return make_pair(tr[u].s, tr[u].mx);
		pushdown(u);
		ll as = 0; int amx = 0;
		if (L <= mid){auto _ = query(ls, L, R); as += _.first; chkmax(amx, _.second);}
		if (R > mid){auto _ = query(rs, L, R); as += _.first; chkmax(amx, _.second);}
		return make_pair(as, amx);
	}
#undef rs
#undef ls
#undef mid
}T;

划分数域

Picks loves segment tree

维护序列 $\{a_n\}$ ， $q$ 次操作：

1 l r v，对于所有 $i\in[l,r]$ 令 $a_i\gets\min\{a_i,v\}$ .

2 l r v，对于所有 $i\in[l,r]$ 令 $a_i\gets a_i+v$ .

3 l r，求 $\sum_{i=l}^ra_i$ .

一种维护两套标记的思路：考虑分别维护最大值和非最大值部分的标记，checkmin 可以看成只对最大值操作，区间加对两种值都操作，于是分别维护最大值的区间加标记和非最大值的区间加标记即可 .

这也就是「划分数域」的思路，将整个数域划分为最大值和非最大值后分别维护 .

可以分析到 $O((n+q)\log^2 n)$ ，比较松上界（如果有别的好 1log 做法最好还是不要划分数域比如那个叫 V 的题目）.

应用：序列（A 层邀请赛 1），UOJ#515 前进四（卡常），CF1290E Cartesian Tree.

AcrossTheSky loves segment tree

维护序列 $\{a_n\}$ ， $q$ 次操作：

1 l r v，对于所有 $i\in[l,r]$ 令 $a_i\gets\min\{a_i,v\}$ .

2 l r v，对于所有 $i\in[l,r]$ 令 $a_i\gets\max\{a_i,v\}$ .

3 l r，求 $\sum_{i=l}^ra_i$ .

把数域分成最大值，最小值和其他，那么分别维护区间和，区间最大值和最小值以及出现次数，次大值和次小值，那么 checkmin 和 checkmax 用传统 seg-beats 方法即可 .

时间复杂度 $O((n+q)\log^2n)$ .

应用：BZOJ4695 最假女选手 . 论文里叫 Mzl loves segment tree 的题目 .

ChiTuShaoNian loves segment tree

维护序列 $\{a_n\},\{b_n\}$ ， $q$ 次操作：

1 l r v，对于所有 $i\in[l,r]$ 令 $a_i\gets\min\{a_i,v\}$ .

2 l r v，对于所有 $i\in[l,r]$ 令 $b_i\gets\min\{b_i,v\}$ .

3 l r v，对于所有 $i\in[l,r]$ 令 $a_i\gets a_i+v$ .

4 l r v，对于所有 $i\in[l,r]$ 令 $a_i\gets b_i+v$ .

5 l r，求 $\max_{i\in[l,r]}\{a_i+b_i\}$ .

数域划分为：同时在 $a,b$ 中是区间最大值的元素，只在 $a,b$ 中一个是区间最大值的元素（这里是两个划分，有点麻烦于是合起来写了）和其他位置 . 那么分别维护标记即可 .

时间复杂度是 $O((n+q)\log^2n)$ ，扩展到 $k$ 个序列就是维护 $2^k$ 套标记（好像叫 Picks loves segment tree VI）.

历史最值问题

双半群模型

半群：对集合 $\cal D$ 和二元运算 $\times$ 满足 $\cal D\times D\to D$ 且 $\times$ 有结合律 .

幺半群：对集合 $\cal D$ 和二元运算 $\times$ 满足 $\cal D\times D\to D$ 且 $\times$ 有结合律，存在单位元 .

交换半群：对集合 $\cal D$ 和二元运算 $\times$ 满足 $\cal D\times D\to D$ 且 $\times$ 有交换律和结合律 .

范围：对于修改查询信息的限制，常见范围：常见的范围有序列区间，树简单路径，二维平面矩形，高维正交范围，半平面范围，圆范围 .

双半群模型：范围修改查询问题的抽象数据结构模型 .

问题描述：

给一个初始集合 $I_0$ ，一个有限集合 $I\sub I_0$ ，询问集合 $Q\sub 2^{I_0}$ 满足 $I_0\in Q$ ，交换半群 $(\mathcal D,+)$ ，半群 $(\mathcal M,*)$ ，二元运算 $\cal\times:D\times M\to D$ .

结合律： $\forall a\in\mathcal D,\,b,c\in\mathcal M,\ (a\times b)*c=a\times(b*c)$ .
分配律： $\forall a,b\in\mathcal D,\,c\in\mathcal M,\ (a+b)\times c=a\times c+b\times c$ .

按顺序执行 $Q$ 个操作，每个操作是修改或者查询操作，第 $t$ 个操作被描述为：

范围修改：给出 $q_t\in Q,\,f_t\in\mathcal M$ ，定义 $d_t(x)=\begin{cases}d_{t-1}(x)*f_t&x\in q_t\\d_{t-1}(x)&\text{otherwise.}\end{cases}$ .
范围查询：给出 $q_t\in Q$ ，定义 $d_t(x)=d_{t-1}(x)$ ，答案为 $\displaystyle\sum_{x\in q_t\cap I}d_t(x)$ .

所有操作和初始权重均离线给出 .

记号： $n=|I|$ 初始权重个数， $q$ 操作数 .

大致来源于 lxl，有小改动 .

那么考虑一个问题要维护的话其实就是构造出 $\mathcal D,\mathcal M$ 和三个运算 $+,*,\times$ .

案例：

NOIP2022 比赛

给序列 $\{a_n\},\{b_n\}$ ， $q$ 次操作，每次给 $l,r$ ，求

$\sum_{p=l}^r\sum_{q=p}^r(\max_{i\in[p,q]}\{a_i\})(\max_{i\in[p,q]}\{b_i\})$

首先初步转化是离线下来右端点排序扫描线，然后维护 $\{a\},\{b\}$ 的单调栈，于是需要维护的问题就是：

维护两个序列 $\{x_n\},\{y_n\}$ ，支持：

对于 $\{x\}$ 或 $\{y\}$ 的区间覆盖操作 .

求区间的历史 $x_i\cdot y_i$ 和 .

那么可以考虑线段树维护 .

大多数情况下传的标记信息都是在维护 $\mathcal D$ 的增量，以及别的什么东西比如区间覆盖啥的 .

于是可以首先注意到区间覆盖的引导，至少要有表示覆盖的标记 $c_x,c_y$ 下传 .

尝试构造 $\mathcal D$ ，观察到 $x_i\times y_i$ 的结构其实看起来要先维护 $\sum x_i,\sum y_i,\sum x_i\cdot y_i$ ，答案 $s$ 和区间长 $len$ ，那么可以记作五元组 $\mathcal D=(s_{xy},s_x,s_y,s,len)$ .

那么考虑修改带来的影响（即考虑标记下传），套路地操作可以设成 $\mathcal M=(c_x,c_y,m_{xy},m_x,m_y,m)$ 表示覆盖标记下传前（显然是要把覆盖的优先级放低一点要不然不好维护）信息对子树中 $s$ 的增量贡献 $m_{xy}\cdot s_{xy}+m_x\cdot s_x+m_y\cdot s_y+m\cdot len$ .

注：此处的「套路地操作」实际上相当于将 $\mathcal D$ 看做行向量， $\mathcal M$ 看做方阵，然后在其上定义广义矩阵乘法等运算 .

根据定义可以验证 $\mathcal D,\mathcal M$ 分别是交换半群和半群 .

于是只需要构造 $\cal D+D\to D,M*M\to M,D\times M\to D$ 即可，其实就是信息合并，标记合并和标记对信息的影响三部分 .

到这里整个双半群模型的用法基本已经明晰了，后面的过程基本就是传统线段树过程就不写了可以看别的题解 .

问题描述

~~懒得写，直接粘论文~~：

使用标记维护的问题

CPU 监控

给一个序列 $\{a_n\}$ ， $q$ 次操作，支持区间覆盖，区间加，区间最大值，区间历史最大值 .

$1\le n,m\le 10^5$ .

考虑设计双半群模型， $\mathcal D$ 直接设成 $\mathcal D=(m,m_h)$ 表示区间最大值和历史最大值就行了，不过 $\mathcal M$ 如果只维护覆盖和加的标记的话 $\cal M*M\to M$ 的时候如果有加负数的情况无法记录历史最大值信息就没法进行了，所以对每个标记引入「历史最大」版本，具体的，构造 $\mathcal M=(c,c',a,a')$ 表示覆盖操作前对 $m$ 的增量为 $a$ ， $m$ 的历史最大增量为 $a'$ ，覆盖操作覆盖为 $c$ ，历史最大覆盖操作为 $c'$ 的信息 .

那么 $\cal D+D\to D,M*M\to M,D\times M\to D$ 都不是很困难了，具体细节可以看一下代码 .

cmd_block 的理解思路是看做维护「标记队列」orz.

CPU 监控

struct SegmentTree
{
#define mid ((tr[u].l + tr[u].r) >> 1)
#define ls (mid << 1)
#define rs (mid << 1 | 1)
	struct Node{int l, r, mx, hmx, cov, ad, had, hcov; bool iscov;}tr[N << 1];
	inline void pushup(int u){tr[u].mx = max(tr[ls].mx, tr[rs].mx); tr[u].hmx = max(tr[ls].hmx, tr[rs].hmx);}
	inline void pcover(int u, int v, int hv)
	{
		tr[u].iscov = true; tr[u].mx = tr[u].cov = v;
		chkmax(tr[u].hcov, hv); chkmax(tr[u].hmx, hv);
	}
	inline void padd(int u, int v, int hv)
	{
		if (tr[u].iscov){pcover(u, tr[u].cov + v, tr[u].cov + hv); return ;}
		chkmax(tr[u].had, tr[u].ad + hv); chkmax(tr[u].hmx, tr[u].mx + hv);
		tr[u].ad += v; tr[u].mx += v;
	};
	inline void pushdown(int u)
	{
		padd(ls, tr[u].ad, tr[u].had); padd(rs, tr[u].ad, tr[u].had); tr[u].ad = tr[u].had = 0;
		if (tr[u].iscov){pcover(ls, tr[u].cov, tr[u].hcov); pcover(rs, tr[u].cov, tr[u].hcov); tr[u].iscov = false; tr[u].cov = -INF;}
	}
	void build(int u, int l, int r)
	{
		tr[u].l = l; tr[u].r = r;
		if (l == r){tr[u].mx = tr[u].hmx = a[l]; return ;}
		build(ls, l, mid); build(rs, mid+1, r);
		pushup(u);
	}
	void add(int u, int L, int R, int v)
	{
		int l = tr[u].l, r = tr[u].r;
		if (inrange(l, r, L, R)){padd(u, v, v); return ;}
		pushdown(u);
		if (L <= mid) add(ls, L, R, v);
		if (R > mid) add(rs, L, R, v);
		pushup(u);
	}
	void cover(int u, int L, int R, int v)
	{
		int l = tr[u].l, r = tr[u].r;
		if (inrange(l, r, L, R)){pcover(u, v, v); return ;}
		pushdown(u);
		if (L <= mid) cover(ls, L, R, v);
		if (R > mid) cover(rs, L, R, v);
		pushup(u);
	}
	pii query(int u, int L, int R)
	{
		int l = tr[u].l, r = tr[u].r;
		if (inrange(l, r, L, R)) return make_pair(tr[u].mx, tr[u].hmx);
		pushdown(u);
		int amx = -INF, ahmx = -INF;
		if (L <= mid){pii _ = query(ls, L, R); chkmax(amx, _.first); chkmax(ahmx, _.second);}
		if (R > mid){pii _ = query(rs, L, R); chkmax(amx, _.first); chkmax(ahmx, _.second);}
		return make_pair(amx, ahmx);
	}
#undef rs
#undef ls
#undef mid
}T;

一些应用（怎么这么多）：SPOJ GSS2，HNOI2016 序列，CF997E Good Subsegments，清华集训2015 V，UOJ#169 元旦老人与数列（数域划分后维护），LuoguP6242 【模板】线段树 3（融合怪）.

posted @ 2023-03-24 11:54 yspm 阅读(476) 评论(6) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 2022.8.22 闲话 — union

· 2022.10.2 闲话

· Segment tree Beats!

· 吉老师线段树

· 线段树进阶笔记

阅读排行：
· winform 绘制太阳，地球，月球运作规律
· TypeScript + Deepseek 打造卜卦网站：技术与玄学的结合
· AI 智能体引爆开源社区「GitHub 热点速览」
· 写一个简单的SQL生成工具
· Manus的开源复刻OpenManus初探

公告

一言（ヒトコト）：

见过我家那只可爱的宠物么？它的名字叫大白。

—— 王者荣耀

昵称： yspm
园龄： 5年1个月
粉丝： 220
关注： 215

+加关注

2025年3月

日

一

二

三

四

五

六

Jijidawang

Jijidawang

Segment Tree Beats! 初步和其他

区间最值问题

不含区间加减的情况

划分数域

历史最值问题

双半群模型

问题描述

使用标记维护的问题

以下是博客签名，正文无关

公告

搜索

常用链接

合集

随笔分类

随笔档案

阅读排行榜

推荐排行榜