2022.11.3 闲话

 

集合论初步

可能会有点混用 $\N$ 和 $\omega$ .

目录

• 集合论初步
  • ZFC 系统
    • 初步建立
    • 走向无穷
    • 顺序的理论基础
  • 基本概念
    • 势
    • 良序与集合比较
  • 投入生产
    • 集合论意义的有序对与关系
    • 冯诺依曼的自然数体系

ZFC 系统

初步建立

公理化系统中对原始概念不作定义，而只给出一些限定条件和定义，并在此基础上进行推理 . 同样，公理集合论中对集合不作定义，它是我们讨论的唯一对象 .

集合间未定义的基本关系（属于）：$A\in B$，可以说 $A$ 是 $B$ 的一个元素 .

以下命题用一阶谓词逻辑表示，因为比较精确且不易产生歧义 . 我觉得读者应该都能把一阶谓词逻辑看懂并翻译 . 有些用谓词写非常繁琐我就用文字了哈 .

定义等于：

「ZFC-1」外延公理 Atom of Extensionality

$$\forall A,B,(\forall x,(x\in A\iff x\in B)\Longrightarrow A=B)$$

「ZFC-2」空集公理 Atom of Extensionality

$$\exists A,\forall x, (x\notin A)$$

空集公理承认不包含任何元素的集合是存在的，这样就避免了追究元素到底是什么，更重要的是，空集公理承认了至少有一个集合存在，这样就有一个构造集合论大厦的开始了 . 根据外延公理，我们可以得到空集唯一，也就是所有空集都相等，这个空集后面就记做 $\varnothing$ 了 .

「ZFC-3」偶集公理 Atom of Pairing

$$\forall a,\forall b,\exists A,\forall x,(x\in A\iff x=a\lor x=b)$$

「ZFC-4」并集公理 Atom of Union

$$\forall M,\exists A,\forall x,(x\in A\iff\exists X(X\in M\land x\in X))$$

偶集公理开始对集合进行打包，构造更上层的集合，并集公理将打好的多个包合并为一个包，实际上就是开始构建 $\cup$ 运算了 .

并集公理配合上偶集公理，可以继续扩展集合元素的数量，于是任何有限集都可在有限步内构造完成 . 要注意，并集公理并不限于两个集合的并 .

下面不加说明，引入运算交 $\cap$，并 $\cup$，差 $-$，二元关系子集 $\subseteq$，真子集 $\subset$ . 这些大家应该都知道 .

一个没啥用的容斥：

$$\left| {\bigcup\limits_{i=1}^n{{A_i}}}\right| =\sum\limits_{k=1}^n{{{(-1)}^{k-1}}\sum\limits_{1\le{i_1}<\cdots<{i_k}\le n}{\left| \bigcap_{j=1}^kA_{i_j}\right| }}$$

「ZFC-5」幂集公理 Atom of Power Set

$$\forall A,\exists P,\forall X,(X\in P\iff X\subseteq A)$$

「ZFC-6」子集公理 Atom Schema of Separation

$$\forall B,\exists A,\forall x,(x\in A\iff x\in B\land C(x))$$

其中 $C(x)$ 是随便一个条件 .

幂集公理和子集公理也是相互配合着的，幂集构建了一个很大的上层集合，为子集公理提供了非常好的限制集 . 子集公理说明集合不能是过于庞大的汇合，这就消除了一些 Native Set Theory 中存在的悖论，例如：

• 一切不属于自己的集合（罗素悖论 / Russell's Paradox）.
• 包含所有集合的集合 .

可以根据子集公理得到，上面两个东西都不存在 .

另外，有些写教材的人非常喜欢花体，于是集合 $A$ 的幂集记做 $\mathscr P(A)$ .

走向无穷

「ZFC-7」无穷公理 Atom of Infinity

$$\exists A,(\varnothing\in A\land (\forall a(a\in A\Longrightarrow a^+\in A)))$$

可能这个式子需要一些注解 . 定义 $a^+=a\cup\{a\}$ 为 $a$ 的后继 (successor)，对于一个包含 $\varnothing$ 的集合，如果它的任意元素的后继还在其中，则它称为归纳集 (inductive set) .

无穷公理其实就表明，至少存在一个归纳集 .

归纳集是我们构造的第一个无穷集，比如自然数就是归纳集 . 但要注意一个归纳集中可能含有自然数之外的的其它元素，需要剔除它们才能得到纯正的自然数集 . 当然，有了一个归纳集作为限制集，加上用子集公理可以这样定义自然数集：

$$\omega=\{n\mid n\in\text{any inductive set}\}$$

我希望你还记得 inductive set 是啥意思 /hsh

归纳原理 Induction Principle

若 $A$ 是 $\omega$ 的一个子归纳集，则 $A=\omega$ .

这表明 $\omega$ 是最小的归纳集，这个归纳原理也就是数学归纳法的基础了 .

关于归纳，我们等会再说，现在进入下一个话题 .

顺序的理论基础

「ZFC-8」选择公理 Atom of Choice

对于一个集簇 $(A_i)_{i\in I}$，选 $a_i\in A_i$，则存在簇 $(a_i)_{i\in I}$ .

带选择公理（AC）的 ZF 体系才叫 ZFC 系统 .

定义存在最小数的全序叫做良序 (well order)，$s(a)=\{x\in A\mid x<a\}$ 称作 $a$ 在 $A$ 中的前段 (initial segment) . 可以知道，对于一个良序，其所有截断（对于线状的全序，截取其左边部分称为截断）都是前段 . 则可以得到：

超限归纳原理 Transfinite Induction Principle

若 $W$ 是良序，$A\subseteq W$ 且 $\forall a, \in W(s(a)\subset A\Longrightarrow a\in A)$，则 $A=W$ .

超限递归定理 Transfinite Recursive Theorem

存在满足递归定义 $u_a=f(u\restriction s(a))$ 的函数 .

P.S. 如果你不认识 $\restriction$ 这个符号，可以看一下「投入生产」部分的「集合论意义的有序对与关系」.

良序的其他内容放在基本概念里了，接下来：

「ZFC-9」替换公理 Atom Schema of Replacement

$$\forall x\in A,\forall y_1,\forall y_2,(\varphi (x,y_1) \land\varphi (x,y_2)\Longrightarrow y_1=y_2)\Longrightarrow\exists B=\{y\mid\exists x,\varphi (x,y)\}$$

「ZFC-10」正则公理 Atom of Regularity

$$\forall A,\exists x,(x\in A\land x\cap A=\varnothing)$$

替换公理非常重要，如果公式恐惧我可以翻译v一下，其实就是「如果给定集合的任一元素都有唯一的集合与之对应，这些集合可以组成集合」，当然这句话也可能有歧义，具体还是看原文最清晰 .

而正则公理则略显多余，它避免了过大集合的产生，但其它 9 条公理其实构造不出那样的集合 . 不过它存在这么长时间了肯定也是有它的道理的啊 .

根据替换公理，可以构造出集合的序数，不过这要到后面说了 .

基本概念

势

定义：存在一一映射的两个集合 $A,B$，称其等势 (equinumerous)，记做 $A\approx B$ .

比如说对于有限集，大小相等就是等势，几个无限集的例子：$f(x)=2x$ 将整数映射到偶数，$f(x)=\cot\pi x$ 将 $(0,1)$ 映射到实数，所以它们都等势 . 也可以理解为「大小相等」.

如果从集合 $A$ 到集合 $B$ 存在单射，则称 $A$ 受制于 $B$，记做 $A\preccurlyeq B$，若与此同时 $A,B$ 不等势，则称 $A$ 严格受制于 $B$，记做 $A\prec B$ .

受二元关系制的良性由 Schröder–Bernstein Theorem（后记 SB 定理）表出：

Schröder–Bernstein Theorem

$$A\preccurlyeq B\land B\preccurlyeq A\Longrightarrow A\approx B$$

这不显然吗

证明有很多，这里就不说了 .

---

利用等势，「有限」和「无穷」就可以被 well-defined 了：和某个自然数等势的集合称为有限集，否则称为无穷集 . 这个自然数是根据集合定义的，其实就和那个后继集一样，定义 $0=\varnothing$，$n^+=n\cup\{n\}$ 就好了，关于自然数，后面再详说 .

这个定义的良性也是需要证明的，即证不同的自然数不等势（归纳一下），从而有限集只与一个自然数等势，这个自然数也叫集合的势，集合 $A$ 的势记做 $N(A)$ .

一个事情：对于 $A\subseteq B$，若有 $N(A)=N(B)$，则 $A,B$ 都是无穷集，否则 $A,B$ 都是有限集，此时 $N(A)>N(B)$ .

定义受制于 $\omega$ 的集合叫可数集，可以证明 $\Z$，$\omega\times\omega$（或者 $\mathbb Q$ 也可以这样表出）等都是可数的 .

这里乘是笛卡尔积，不知道可以看一下「投入生产」.

证明 $\omega\times\omega$ 是可数集是很经典的，大家都知道 Cantor 表吧！

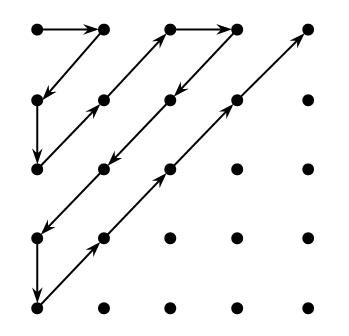
证明 $\mathbb R$ 是不可数的：对角论证，懒得说了 .

$\omega$ 的势一般用 $\aleph_0$ 表示，$\R$ 的势一般用 $C$ 表示（注意这里还不是 $\aleph_1$），根据二进制表出浮点数则可以得到 $\R\approx 2^{\omega}$，也就是 $C=2^{\aleph_0}$ .

显然 $\aleph_0$ 是最小的无穷势，假设下一个无穷势记作 $\aleph_1$，则是否有 $\aleph_1=C$？

更一般的，

连续统假设

$$\forall \alpha\in\mathbb N_+,\aleph_{\alpha+1}=2^{\aleph_{\alpha}}$$

大家有兴趣可以证一下！Gödel 和 Cohen 先后证明了连续统假设和 ZFC 兼容且独立，也就是说，ZFC 中连续统假设是不可证明的 . 虽然至今仍未找到合适的公理系统使其成立（即可被证明）.

良序与集合比较

对于良序 $(X,\le_X),(Y,\le_Y)$，如果存在双射 $f:X\to Y$ 使得 $a\leqslant _Xb\iff f(a)\leqslant _Yf(b)$，则称 $X,Y$ 相似 (isomorphic)，记作 $X \simeq Y$ .

可以发现，良序到其子集的相似映射总有 $x\le f(x)$（感性理解一下还是挺直观的），进而可以得出良序不能和其截断相似和良序间相似映射的唯一性 .

良序比较：因为由超限递归原理容易证明它们要么相似，要么一个相似于另一个的前段，所以对齐头部看一下长度就完了 .

良序化原理 Well-ordering Theorem

任何集合都可以良序化 .

证明略 . 于是因为任何集合可以良序化，而良序集可较，所以任何集合可较 .从而有三歧性：$A\approx B$，$A\prec B$，$B\prec A$ 恰有一个成立 .

推论：

Zorn 引理

如果序集的任意链有上界，则它有极大值 .

把序集良序化然后一波操作即可 . 事实上，选择公理、良序原理和 Zorn 引理可以看做是等价的 .

---

顺序已经构造好了，现在可以标号了 . 定义满足 $\forall x\in\alpha,(s(x)=x)$ 的良序集 $\alpha$ 称为序数 .

序数唯一性：显然归纳一下可以得到所有自然数都是序数，进一步用超限归纳原理还可以证明相似的序数必是相等的，序数唯一性也就能证了 .

序数都是良序集，它们也就满足三歧性，所以它们可以一字排开，而且每个序数还可以定义后继（其实也是 $a\cup\{a\}$ 的形式）.

提问：所有集合都有其对应的序数吗？

考察良序集中那些有序数的前段，这些序数的并（替换公理）就是要找的序数 .

计数原理

任何良序集 $X$ 都相似于唯一序数 $\alpha=\operatorname{ord}(X)$ .

序数可以作为自然数的扩展，不是自然数的序数叫超限数，可以按如下方法定义序数的加法和乘法，它们满足大部分运算定律，但乘法不满足交换律和右分配律：

1. $\alpha +\beta ={\rm ord}(\{(x,0)\mid x\in\alpha\}\cup\{(1,x)\mid x\in\beta\})$ .
2. $\alpha\cdot\beta ={\rm ord}(\alpha\times\beta )$ .

序数仅能扩展自然数「序」的性质，但却不能体现「量」的性质，因为不同的序数可以是等势的 . 这些等势的序数有最小者，把它作为「量」的度量，称为基数 (cardinal number)，$X$ 的基数记做 $\operatorname{card}(X)$ .

基数是势的量化描述，非自然数的基数称为超限基数，显然最小的超限基数是 $\aleph_0$ .

由序数原理自然可知每个序集都有都有对应基数，这样 SB 定理变得非常显然，不过这个证明依赖于选择公理 AC，有点遗憾 .

基数的加法、乘法和幂都容易定义，以及一般的运算律都容易证明 . 通过 Zorn 引理和反证法可以得到（以下 $b$ 均为超限基数）：

• 加法吸收律：若 $a\le b$，则 $a+b=b$ .
• 乘法吸收律：若 $1\le a\le b$，则 $a\cdot b=b$ .
• 幂的降底律：若 $2\le a\le b$，则 $a^b=2^b$ .

后面还能探索很远啊……你可以试试，说不定就菲尔兹奖了呢？

投入生产

集合论意义的有序对与关系

有序对 (ordered pairs) 的集合论表出：$(a,b)=\{a,\{a,b\}\}$，可以发现确实是有序的！

笛卡尔积 $A\times B$ 在限制集 $\mathscr P(A\cup B)$ 定义为 $A\times B=\{(a,b)|a\in A\land b\in B\}$ .

---

现在定义关系，关系可能是离散数学的内容吧 . 定义：只包含有序对的集合叫关系（其实这个应该是定义的二元关系，你开心就好）.

然后就是定义关系的定义域 $\operatorname{dom}(R)$，值域 $\operatorname{ran}(R)$，逆 $R^{-1}$ 和复合 $R\circ S$，还有我们熟悉的函数概念，$X$ 到 $Y$ 的一切函数组成的集合记做 $Y^X$，然后还有单射、满射、双射（一一映射）的概念，以及象和原象 .

$F$ 的限制 (restriction) $F\restriction A$ 定义为 $F\restriction A =\{(x,y) \in F\mid x\in A\}$ .

冯诺依曼的自然数体系

定义：$0=\varnothing$，$n^+=n\cup\{n\}$ .

接下来需要验证这样的自然数集是否合理，首先验证是否任意两个自然数 $a,b$ 都可比，满足三歧性：$a=b$，$a<b$，$b<a$ 恰有一个成立 .

根据数学归纳法可以得到 $a\in b$ 或 $a\subset b$ 即可作为 $a<b$ 的一个定义 .

排序后，自然数序列有开头而没有结尾，这个简单的性质使之区别于其它数集，而且也是后面扩展为超限数的基础 . 这个性质一般表现为：

最小数定理

$$\forall S\subseteq\mathbb N,\exists x\in S,\forall y\in(S-\{x\}),x<y$$

证明很简单，不说了 .

类似于自然数的定义，有一种常见的递归序列 $u_{n^+}=f(u_n)$，序列的后一项依赖于前一项，这样的序列能否成为集合？直觉上看它和自然数集本质上是相同的，只要证明存在一个从自然数集到该序列的函数即可，这就是递推原理 (Recursive Theorem) . 虽然这个函数有明显的限制集，但由于是递归定义的，无法用有限的条件来描述它，所以简单地用子集公理是不行的 .证明方法和自然数集的定义是类似的，即找寻满足条件的关系中最小那个（所有关系的交集），继而只要用归纳原理证明它满足递归条件且是函数即可 .

有了递推原理，就可以按如下递归的方法定义自然数上的诸多二元运算，它们都是 $F:\omega\times\omega\to\omega$ 上的函数 ：

1. $a+0=a$，$a+b^+=(a+b)^+$ .
2. $a\cdot 0=0$，$a\cdot b^+=a\cdot b+a$ .
3. $a^0=1$，$a^{b^+}=a^b\cdot b$ .

可以根据定义验证其普通性质 .

第二归纳法：

第二归纳原理 Second Induction Principle

集合 $A\subseteq \N$ 若满足 $\forall x \in \N,(x<n\Longrightarrow x\in A)\iff n\in A$，则 $A=\omega$ .

第二递归定理 Second Recursive Theorem

存在满足递归定义 $u_n=f(u\restriction n)$ 的函数 .

是不是很像超限归纳原理和超限递归原理？

这样 $\N$ 就构建好了，也可以轻松以此为基础构建 $\Z$ 和 $\mathbb Q$ .

关于构建 $\R$ 啊，历史上有两个优秀的实数模型，一个来自康托尔的战友戴德金，一个来自康托尔 . 戴德金分割将一个实数定义为有理数集的一个分割，这个简单而有效的定义非常适合于实数运算；康托尔则用无穷有理数列定义实数，本质是将实数定义为实无穷 . 不说了，再说跑题了 .