2022.11.2 闲话

SoyTony 大定理：

$$\begin{bmatrix}1\\&1\\&&1\\&&&\ddots\\&&&&1\end{bmatrix}=-32+\mathrm i=\begin{pmatrix}1&2&3&4&\cdots&n\\1&2&3&4&\cdots&n\end{pmatrix}$$

---

SoyTony 的歌词

Y.M.C.A.

Young man, theres no need to feel down.
I said, young man, pick yourself off the ground.
I said, young man, cause youre in a new town
Theres no need to be unhappy.
Young man, theres a place you can go.
I said, young man, when youre short on your dough.
You can stay there, and Im sure you will find
Many ways to have a good time.
Its fun to stay at the Y-M-C-A.
Its fun to stay at the Y-M-C-A.
They have everything for you men to enjoy,
You can hang out with all the boys ...
Its fun to stay at the Y-M-C-A.
Its fun to stay at the Y-M-C-A.
You can get yourself cleaned, you can have a good meal,
You can do whatever you feel ...
Young man, are you listening to me?
I said, young man, what do you want to be?
I said, young man, you can make real your dreams.
But you got to know this one thing!
No man does it all by himself.
I said, young man, put your pride on the shelf,
And just go there, to the Y-M-C-A.
Im sure they can help you today.
Its fun to stay at the Y-M-C-A.
Its fun to stay at the Y-M-C-A.
They have everything for you men to enjoy,
You can hang out with all the boys ...
Its fun to stay at the Y-M-C-A.
Its fun to stay at the Y-M-C-A.
You can get yourself cleaned, you can have a good meal,
You can do whatever you feel ...
Young man, I was once in your shoes.
I said, I was down and out with the blues.
I felt no man cared if I were alive.
I felt the whole world was so tight ...
Thats when someone came up to me,
And said, young man, take a walk up the street.
Theres a place there called the Y-M-C-A.
They can start you back on your way.
Its fun to stay at the Y-M-C-A.
Its fun to stay at the Y-M-C-A.
They have everything for you men to enjoy,
You can hang out with all the boys ...

三角形垂心存在性

全等相似那些 Method 我不会 .

目录

• 三角形垂心存在性
  • Method 1
  • Method 2
  • Method 3
  • Method 4

Method 1

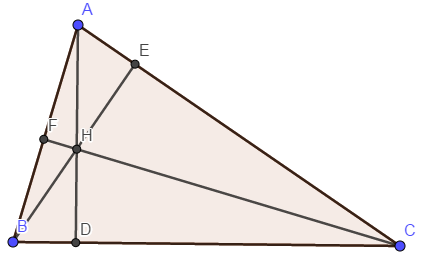
熟知：

角元塞瓦定理

有一三角形 $\triangle ABC$ 和三个点 $D,E,F$，有 $D,E,F$ 与 $\triangle ABC$ 在同一平面内且均不在三角形三边所在直线上，则 $AD,BE,CF$ 三线共点当且仅当

$$\dfrac{\sin\angle BAD}{\sin\angle CAD}\cdot \dfrac{\sin\angle ACF}{\sin\angle BCF}\cdot \dfrac{\sin\angle CBE}{\sin\angle ABE}=1$$

于是因为显而易见的

$$\begin{aligned}&\dfrac{\sin\angle BAD}{\sin\angle CAD}=\dfrac{\sin(\frac{\pi}2-\angle B)}{\sin(\frac{\pi}2-\angle C)}=\dfrac{\cos B}{\cos C}\\&\dfrac{\sin\angle ACF}{\sin\angle BCF}=\dfrac{\sin(\frac{\pi}2-\angle A)}{\sin(\frac{\pi}2-\angle B)}=\dfrac{\cos A}{\cos B}\\&\dfrac{\sin\angle CBE}{\sin\angle ABE}=\dfrac{\sin(\frac{\pi}2-\angle C)}{\sin(\frac{\pi}2-\angle A)}=\dfrac{\cos C}{\cos A}\end{aligned}$$

三式相乘显然得 $1$ .

证毕 .

Method 2

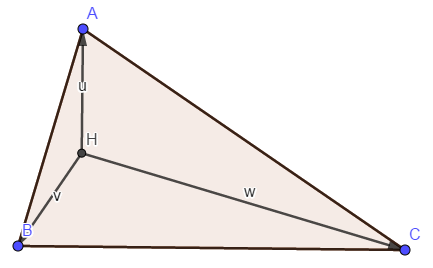
令 $\overrightarrow{HA}=\overrightarrow u$，$\overrightarrow{HB}=\overrightarrow v$，$\overrightarrow{HC}=\overrightarrow w$ .

假设现在已知 $HA\perp BC$，$HB\perp AC$，欲证 $HC\perp AB$ .

于是显而易见 $(\overrightarrow u-\overrightarrow v)\overrightarrow w=0$，$(\overrightarrow v-\overrightarrow w)\overrightarrow u=0$ .

两式相加即可得到 $(\overrightarrow u-\overrightarrow v)\overrightarrow v=0$，翻译一下就是 $HC\perp AB$，证毕 .

还确实挺简洁的啊！

Method 3

建系！如图，以 $AB$ 为 $x$ 轴，$AB$ 对应的高为 $y$ 轴建立平面直角坐标系：

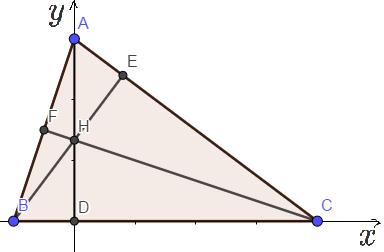
这样就只需要证明 $BE,CF$ 交点在 $y$ 轴上 .

然后就只需要求 $BE,CF$ 的解析式了，有 $AB,AC$ 的解析式就随便求了吧 .

后面都是 dirty-works，不想写了，直接证毕了！

Method 4

假装我们已经得到了外心存在性（其实也挺水的这个），然后就得到的是三条中垂线交点是外接圆圆心 .

反向构造一个中点三角形，如图：

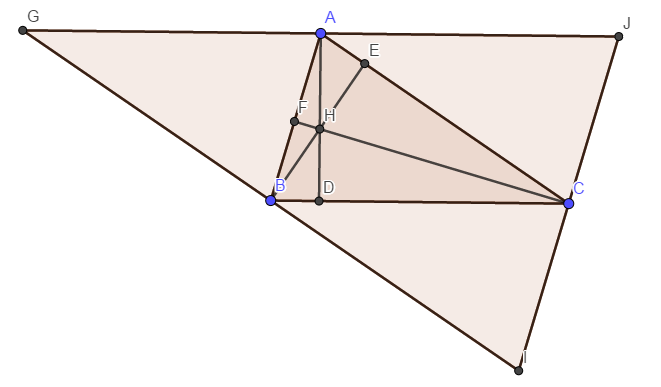
于是问题就变成了这样：

已知 $CF,BE,AD$ 是 $\triangle GIJ$ 的三条中垂线，交于点 $H$，$B,C,A$ 分别是 $GI,IJ,JG$ 的中点，求证：$CF,BE,AD$ 是 $\triangle ABC$ 的三条高 .

证明就大概是因为 $A$ 是 $JG$ 中点，$C$ 点是 $IJ$ 中点，所以 $AC//GI$ . 又 $GI\perp BE$，所以 $AC\perp BE$，于是 $BE$ 就是 $AC$ 边上的高了 .

剩下两个同理，然后就证完了 .

一个类似的是把三角形的类似重心规约到切心 .