Jijidawang

2022.11.1 闲话

原来还打算写一个包含三个树上博弈的闲话，不过懒得写了 .

在没人看的闲话里推流没人看的游记：CSP 游记 .

UPD. SoyTony 歌词

Save Me

It started off so well
They said we made a perfect pair
I clothed myself in your glory and your love
How I loved you
How I cried
The years of care and loyalty
Were nothing but a sham it seems
The years belie we lived the lie
"I love you 'til I die"
Save me, Save me, Save me
I can't face this life alone
Save me Save me Save me
I'm naked and I'm far from home
The slate will soon be clean
I'll erase the memories
To start again with somebody new
Was it all wasted
All that love ?
I hang my head and I advertise
A soul for sale or rent
I have no heart, I'm cold inside
I have no real intent
Save me, Save me, Save me
I can't face this life alone
Save me Save me
Oh I'm naked and I'm far from home
Each night I cry and still believe the lie
I love you 'til I die
(Save me, Save me, Save me)
Yea, yeah
Save me yeah Save me oh Save me
Don't let me face my life alone
Save me, Save me
Oh I'm naked and I'm far from home

魔法少女とチョコレゐト / 魔法少女与巧克力

Я　らりぱっぱらぱっぱっぱらっぱ
Я 啦哩啪啪啦啪啪啪啦啪

らりぱっぱらぱっぱっぱらっぱ
啦哩啪啪啦啪啪啪啦啪

純粋が仇になる世界で
在这个纯洁使我们自食其果的世界上

Я　らりぱっぱらぱっぱっぱらっぱ
Я 啦哩啪啪啦啪啪啪啦啪

らりぱっぱらぱっぱっぱらっぱ
啦哩啪啪啦啪啪啪啦啪

また来週も戦えるかな
可否下周再战？

可愛い衣装まとって
我穿上可爱的衣服

決めポーズで光って
摆好姿势散发光芒

ピュアな想い　魔法に変えて
将我纯洁的感情 转变成魔法

みんなの平和願って
祈愿大家的和平

邪悪に立ち向かって
勇敢面对邪恶

それを匿名はディスった
匿名之人却指责道

「本当は〇〇なんでしょ？」
「你真〇〇啊，不是吗？」

「ぶっちゃけ〇〇なんでしょ？」
「不开玩笑，难道不〇〇吗？」

自分がそう思うから
因为这就是你所深信着的

みんな〇〇であって欲しいんでしょ
你只是觉得每个人都〇〇吧

そんな手垢のついた
带着你们那老一套

よくある風評で
司空见惯的谣言

錆びつく魔法のステッキ
魔法棒渐渐染上锈迹

知らん　知らん
不知道 不知道

はぁ　正直もうやめたい（はぁ）
唉 说真的已经累了（唉）

魔法少女をやめたい（はぁ）
不想再当魔法少女了（唉）

誰が敵か味方かわかんないし
毕竟我已分不清孰敌孰友

「陰険」で　「強欲」で
「阴险」 「贪婪」

「滑稽」で　「外道」で
「滑稽」 「异端」

魔法がとけるチョコみたいに
如同将魔法融化的巧克力一般

Я　らりぱっぱらぱっぱっぱらっぱ
Я 啦哩啪啪啦啪啪啪啦啪

らりぱっぱらぱっぱっぱらっぱ
啦哩啪啪啦啪啪啪啦啪

純粋が仇になる世界で
于此被我们的纯洁所反噬的世界之中

はぁ　正直もうやめたい（はぁ）
唉 说真的想放弃了（唉）

魔法少女をやめたい（はぁ）
不愿再做魔法少女了（唉）

もう　好きな人だけ守っていたい
我只愿守护我所爱之人

Я　だんだんでぃだん
Я 铛铛滴铛

だんだんでぃだん
铛铛滴铛

Я　だんだんでぃだんだんだんでぃ
Я 铛铛滴铛铛铛滴

だんだんと身勝手になる
我变得越来越自私

魔力が煮え立つ
魔法也随之沸腾

不満で調合したポーションがパリン
混合了不满的药水砰地一声

「お前ら〇〇なんでしょ？」
「你们都是〇〇吧？」

「性根が〇〇なんでしょ？」
「本质上也就是〇〇吧？」

怒りにまかせ
任凭愤怒

脳内で〇〇しちゃうでしょう
在脑内〇〇了吧

やり返しはナンセンス
报复只是无稽之谈

気に病んでもスルーです
烦恼全部抛在一边

光失ったブローチ
胸针变得黯淡无光

腐る　腐る
堕落 堕落

はぁ　正直もうやめたい（はぁ）
唉 说真的已经累了（唉）

魔法少女をやめたい（はぁ）
不想再当魔法少女了（唉）

視聴者の期待に応えるたびに
每当我回应观众的期望

「完璧」で　「超人」で
「完美」 「超人」

「清廉」で　「潔白」で
「清廉」 「无辜」

嘘で固めたチョコみたいに
好似被谎言所掩盖的巧克力一般

Я　らりぱっぱらぱっぱっぱらっぱ
Я 啦哩啪啪啦啪啪啪啦啪

らりぱっぱらぱっぱっぱらっぱ
啦哩啪啪啦啪啪啪啦啪

甘い味が病みつきでしょう
这丝甜蜜真令人着迷啊

はぁ　正直もうやめたい（はぁ）
唉 说真的想放弃了（唉）

魔法少女をやめたい（はぁ）
不愿再做魔法少女了（唉）

「やめないで」って言われんの
你还在期待着大家会说

期待してない？
「请留下来」吗？

ファンの善意の〇〇も
粉丝们的善意的〇〇

心配してる〇〇も
和担心的〇〇

〇〇〇〇〇！！
〇〇〇〇〇！！

すべて耳を塞いでしまったの
对此全部充耳不闻

はぁ　正直もうやめたい（はぁ）
唉 说真的已经累了（唉）

魔法少女をやめたい（はぁ）
不想再当魔法少女了（唉）

誰が敵か味方かわかんないし
因为我早已分不清孰敌孰友

「陰険」で　「強欲」で
「阴险」 「贪婪」

「滑稽」で　「外道」で
「滑稽」 「异端」

魔法がとけるチョコみたいに
如同将魔法融化的巧克力一般

Я　らりぱっぱらぱっぱっぱらっぱ
Я 啦哩啪啪啦啪啪啪啦啪

らりぱっぱらぱっぱっぱらっぱ
啦哩啪啪啦啪啪啪啦啪

魔法で最低な人を消そう
用魔法将恶人全部抹消

はぁ　正直もうやめたい（はぁ）
唉 说真的已经累了（唉）

魔法少女をやめたい（はぁ）
不想再当魔法少女了（唉）

自分ごと消えちゃって　さようなら
连同自己也一起抹除 永别

Я　らりぱっぱらぱっぱっぱらっぱ
Я 啦哩啪啪啦啪啪啪啦啪

らりぱっぱらぱっぱっぱらっぱ
啦哩啪啪啦啪啪啪啦啪

純粋が仇になる世界で
在这个与纯洁为仇的世界里

Я　らりぱっぱらぱっぱっぱらっぱ
Я 啦哩啪啪啦啪啪啪啦啪

らりぱっぱらぱっぱっぱらっぱ
啦哩啪啪啦啪啪啪啦啪

また来週も観てくれるかな
下周还会来看我吗

今天是 11 月的第一天啊 .

目录

理性理解凸透镜成像规律

透镜的高斯成像公式：

\[\dfrac 1u+\dfrac 1v=\dfrac 1f \]

或者说 \(f\) 是 \(u,v\) 的调和平均值 .

证明到处都有，就不说了 .

成实像当且仅当 \(u+v\ge 4f\) .

\(u\in(2f,+\infty)\)

\[v=\dfrac1{\dfrac1f-\dfrac 1u}<\dfrac1{\dfrac1f-\dfrac1{2f}}=2f \]

当 \(u\to\infty\) 时 \(v\to f\)（右侧）.

故可得 \(u\in(2f,+\infty)\) 时，\(v\in(f,2f)\) .

\(u=2f\)

\[v=\dfrac1{\dfrac1f-\dfrac 1u}=\dfrac1{\dfrac1f-\dfrac1{2f}}=2f \]

故可得 \(u=2f\) 时，\(v=2f\) .

\(u\in(f,2f)\)

\[v=\dfrac1{\dfrac1f-\dfrac 1u}>\dfrac1{\dfrac1f-\dfrac1{2f}}=2f \]

\[v=\dfrac1{\dfrac1f-\dfrac 1u}<\dfrac1{\dfrac1f-\dfrac1f}=+\infty \]

故可得 \(u\in(f,2f)\) 时，\(v\in(2f,+\infty)\) .

\(u=f\)

\[v=\dfrac1{\dfrac1f-\dfrac 1u}=\dfrac1{\dfrac1f-\dfrac1f}=+\infty \]

故可得 \(u=f\) 时，\(v=\infty\) 也就是不成像 .

因为凸透镜不能发散光，于是此时形成的是平行光 .

\(u\in(0,f)\)

\[v=\dfrac1{\dfrac1f-\dfrac 1u}<\dfrac1{\dfrac1f-\dfrac1f}=+\infty \]

\(u\to 0\) 时，\(v\to 0\) .

故可得 \(u\in(-\infty,f)\) 时，\(v\in(0,+\infty)\) .

？？？你玩我呢？

那么尝试得到一个更紧一点的界 .

\[v=\dfrac1{\dfrac1f-\dfrac 1u}=\dfrac{fu}{f-u}=\dfrac f{f-u}u \]

因为 \(u\in(0,f)\) 所以 \(\dfrac f{f-u}\in(1,+\infty)\) .

于是 \(v\in(u,+\infty)\)，这个界还不错是不是？

凸透镜成像规律

物距 \(u\) 像距 \(v\) 正倒 大小 虚实 位置关系 常见应用
\((2f, +\infty)\) \((f, 2f)\) 倒立 缩小 实像 物像异侧 照相机，摄像机
\(2f\) \(2f\) 倒立 等大 实像 物像异侧 测焦距
\((f, 2f)\) \((2f, +\infty)\) 倒立 放大 实像 物像异侧 幻灯机，电影，放映机，投影仪
\(f\) \(+\infty\) 不成像 不成像 不成像 不成像 强光聚焦手电筒
\((0, f)\) \((u, +\infty)\) 正立 放大 虚像 物像同侧 放大镜

副光轴作图法正确性证明

问题概述

给一个凸透镜，由光心，主光轴和两焦点表示，又给一条入射光线，作出其出射光线 .

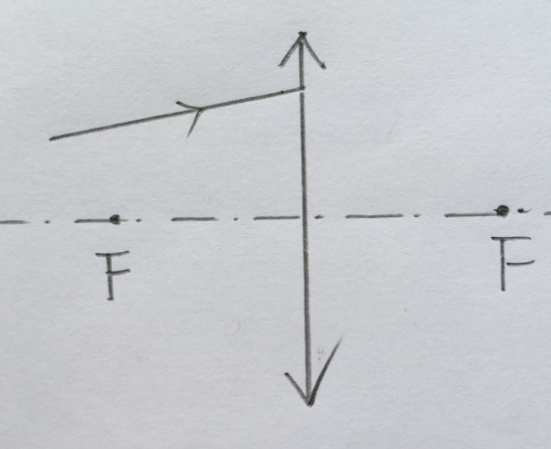
特殊光线法 / 成像法

首先在光线上随便取一点 \(A\)，可以做出其过凸透镜成的像，然后连接即可 .

副光轴法

过光心作入射光的平行线（即副光轴），然后等价的焦点就在原焦点的正上方（即作垂线）.

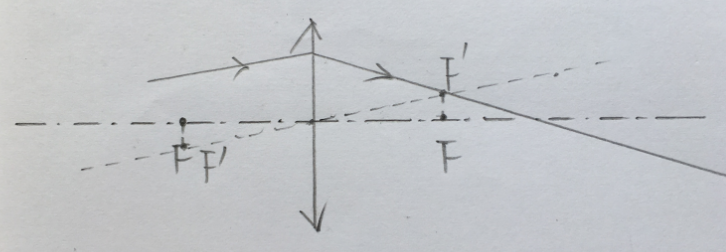
特殊光线法的正确性显然，现在试图证明特殊光线法则副光轴法正确：

左边的焦点叫 \(F_1\)，右边是 \(F_2\)，如图：

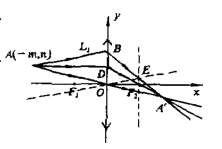
考虑特殊光线法的流程，首先在光线上随便取一点 \(A(-m,n)\)，直接解析，经过特殊光线法的 dirty-works 可以得到其像为 \(A'\left(\dfrac{fm}{m-f},-\dfrac{fn}{m-f}\right)\) .

令过 \(A\) 点的任一直线 \(\ell:y-n=k(x+m)\) 与凸透镜的交点坐标为 \(B(0,km+n)\)，\(A'B\) 所在直线与过焦点 \(F_2\) 的焦平面交于点 \(E\)，则可得 \(A'B\) 的解析式为 \(y-km-n=\dfrac{(km+n)(n-f)+fn}{fm}\)，进而可得 \(E\) 点坐标为 \((f,kf)\) .

从而 \(OE\) 的解析式为 \(y=kx\)，也就得到了平行于副光轴的光线折射后过副焦点交于像点 \(A'\)，证毕 .

其实这两个方法是完全等价的，具体可以看《中学物理》上的《副光轴作图法与特殊光线作图法等价》.

posted @ 2022-11-01 10:29  Jijidawang  阅读(167)  评论(1)  编辑  收藏  举报
😅​