2022.10.5 闲话

DTOI 感觉很强，膜拜 joke3579 .

只不过说好的数学题呐？咋变成三维偏序啦？

---

目录

• EntropyIncreaser 与菱形计数
  • 题面
  • 转换为三维问题
  • 转换为不相交路径计数
  • 应用半标准杨表的 Hook 公式
• ZJOI2022 计算几何

图源：

• https://loj.ac/p/6677 .
• https://www.cnblogs.com/psimonw/p/11454899.html .

EntropyIncreaser 与菱形计数

题面

求将边长为 \(a,b,c\) 的六边形分解成若干个小菱形的方案数，对某个素数取模 .

\(a, b, c\le 10^6\) .

转换为三维问题

相当于一个 \(a\times b\) 的网格，每个格子上可以堆至多 \(c\) 个方块，并且每个格子的方块数量不能超过它左边和上面的格子的方块数量 .

然后这样就看起来比较可做了，接下来我们大概有两条路可走 .

转换为不相交路径计数

将这个问题再转化为一个二维问题：从右上角的所有格子往左下角的所有格子对应着走，且不相交的方案数 .

转换过程和半标准杨表差不多 .

具体的

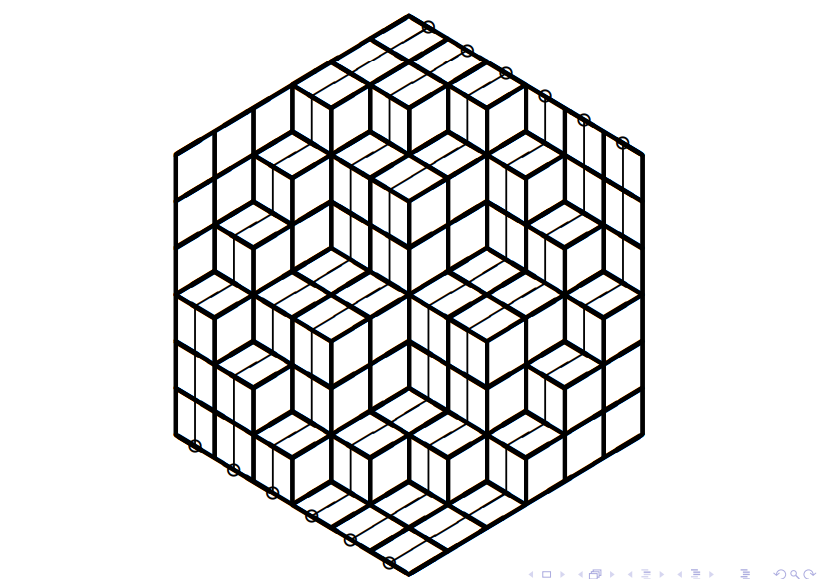
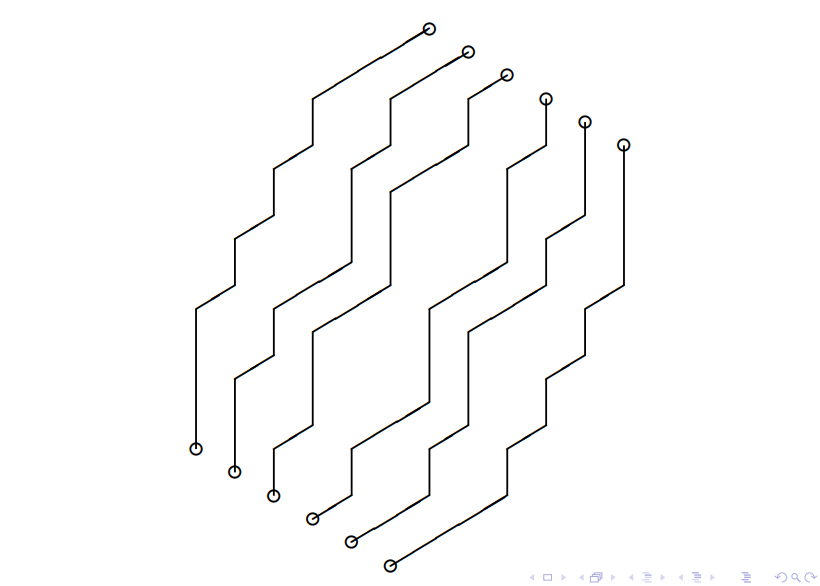
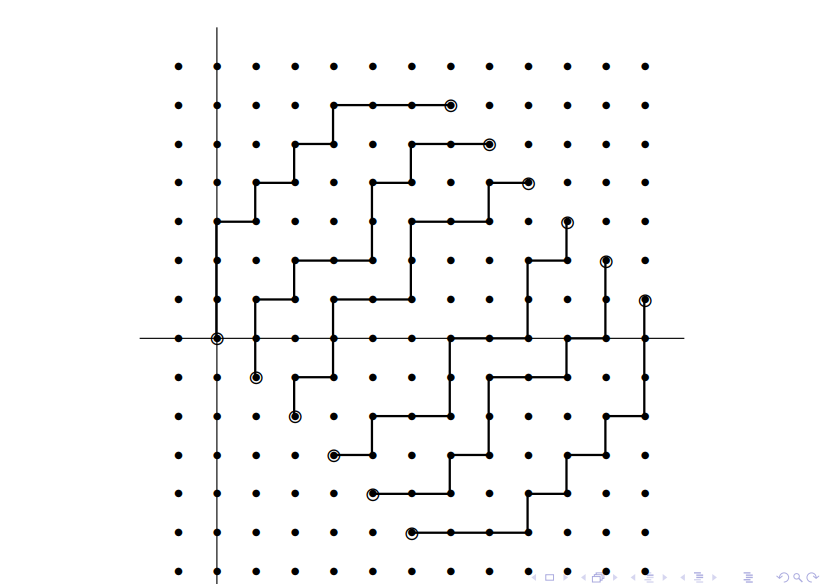
然后就可以用 LGV 引理解决了 .

然后答案就是（下面的矩阵只有第一个完整写开）

\[\begin{aligned}ans&=\det\left(\begin{bmatrix}\binom{a+b}a&\binom{a+b}{a-1}&\cdots&\binom{a+b}{a+1-c}\\\binom{a+b}{a+1}&\binom{a+b}a&\cdots&\binom{a+b}{a+2-c}\\\vdots&\vdots&\ddots&\vdots\\\binom{a+b}{a+c-1}&\binom{a+b}{a+c-2}&\cdots&\binom{a+b}a\\\end{bmatrix}\right)\\&=\det\left(\prod_{k=j+1}^c(a+k-i)\prod_{k=2}^j(b+i-k+1)\right)_{i,j=1}^c\cdot\prod_{i=1}^c\dfrac{(a+b)!}{(a+c-i)!(b+i-1)!}\\&=\det\left(\prod_{k=j+1}^c(a+k-i)\prod_{k=2}^j(k-b-i-1)\right)_{i,j=1}^c\cdot(-1)^{\frac{c(c-1)}2}\prod_{i=1}^c\dfrac{(a+b)!}{(a+c-i)!(b+i-1)!}\end{aligned} \]

Krattenthaler's Formula

\[\det\left(\prod_{k=2}^j(x_i+a_k)\prod_{k=j+1}^m(x_i+b_k)\right)_{i,j=1}^n=\prod_{1\le i<j\le n}(x_i-x_j)\prod_{2<i\le j\le n}(a_i-b_j) \]

于是

\[\det\left(\prod_{k=j+1}^c(a+k-i)\prod_{k=2}^j(k-b-i-1)\right)_{i,j=1}^c=\prod_{1\le i<j<c}(j-i)\prod_{2\le i\le j\le c}(a+b+j-i-1) \]

代入，令 \(\displaystyle F(k)=\prod_{i=0}^ki!\)，则

\[\begin{aligned}\mathrm{answer}&=\prod_{1\le i<j<c}(i-j)\prod_{2\le i\le j\le c}(a+b+j-i-1)\prod_{1\le i\le c}\dfrac{(a+b)!}{(a+c-i)!(b+i-1)!}(-1)^{\frac{c(c-1)}2}\\&=\prod_{i=1}^{c-1}i!\prod_{i=1}^{c-1}\dfrac{(a+b+i)!}{(a+b)!}\prod_{i=1}^c(a+b)!\prod_{i=1}^c\dfrac1{(a+c-i)!}\prod_{i=1}^c\dfrac1{(b+i-1)!}\\&=\dfrac{F(a)F(b)F(c)F(a+b+c)}{F(a+b)F(b+c)F(a+c)}\end{aligned} \]

直接算一下就是 \(\Theta(a+b+c)\) 的时空复杂度了 .

如果实现不优秀可能带一个求逆元的 log，都能过 .

发现这条路需要高超的代数技巧 . 我们看看另一条路 .

应用半标准杨表的 Hook 公式

形式化一下题面，就是一个 \(a\times b\) 矩形 \(h\)，满足：

• \(h_{i,j}\in[0,c]\cap\mathbb Z\) .
• \(h_{i,j}\le h_{i+1,j}\) .
• \(h_{i,j}\le h_{i,j+1}\) .

令 \(g_{i,j}=h_{i,j}+i\)，则

• \(h_{i,j}\in[1,a+c]\cap\mathbb Z\) .
• \(h_{i,j}<h_{i+1,j}\) .
• \(h_{i,j}\le h_{i,j+1}\)（因为只是加了一个 \(i\) 所以这里的约束还是 \(\le\)）.

这样显而易见 \(g,h\) 在这样的约束下构成双射，我们只需要计数 \(g\) .

可见 \(g\) 是一个半标准杨表 .

众所周知：

半标准杨表计数

\[f'_{\lambda}=\prod_{1\le i<j\le m}\dfrac{\lambda_i-i-\lambda_j+j}{j-i} \]

然后直接代入，进行一些朴素的变换就可以得到答案是

\[\dfrac{F(a)F(b)F(c)F(a+b+c)}{F(a+b)F(b+c)F(a+c)} \]

其中 \(\displaystyle F(k)=\prod_{i=0}^ki!\)，殊途同归 .

时空复杂度仍然是 \(\Theta(a+b+c)\) .

ZJOI2022 计算几何

九条可怜是一个喜欢计算几何的女孩子，她画了一个特别的平面坐标系，其中 \(x\) 轴正半轴与 \(y\) 轴正半轴夹角为 \(60\) 度 .

从中，她取出所有横纵坐标不全为偶数，且满足 \(-2 a + 1 \le x \le 2 a - 1\)，\(-2 b + 1 \le y \le 2 b - 1\)，\(-2 c + 1 \le x + y \le 2 c - 1\) 的整点 .

可怜想将其中一些点染色，但相邻的点不能同时染色 . 具体地，对于点 \((x, y)\)，它和 \((x, y + 1), (x, y - 1), (x + 1, y), (x - 1, y), (x + 1, y - 1), (x - 1, y + 1)\) 六个点相邻，可结合样例解释理解 .

可怜想知道在这个规则下最多能将多少点染色，以及染最多点的染色方案数 . 由于后者值可能很大，对于染色方案数，你只需要输出对 \(p=998244353\) 取模后的结果 . 注意不需要将最多染色点数取模 .

\(a,b,c\le 10^6\) .

首先转换一下题意，用样例解释的图来转换就是：

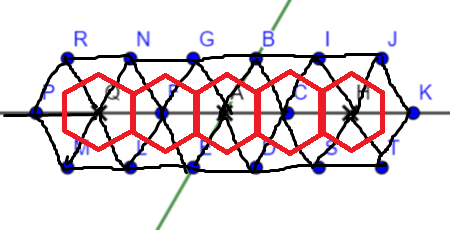
注意这样只有非平凡情况，也就是 \(a+b>c\) 的时候能转换 .

这样问题就是求那个红色部分的最大独立集，实际上可以和平面的立方体凸堆叠建立双射，就和 EntropyIncreaser 与菱形计数那个题一样了 .

通过一些观察可以发现这个题的 \(a,b,c\)（后面记作 \(a',b',c'\)）实际上就是原题中的 \(a+b-c\)，\(a+c-b\) 和 \(b+c-a\)，它们是对称式，这也印证了这个做法的正确性 .

显然存在完美匹配，于是最多的点数就是 \(a'b'+b'c'+c'a'\) .

根据 EntropyIncreaser 与菱形计数的结论可以直接解决第二问 .

前面忽略的 \(a+b\le c\) 的平凡情况，就是一个平行四边形，不难发现答案就是 \(4ab\) 和 \(1\) .

时间复杂度 \(\Theta(a+b+c+T)\) 或 \(\Theta(a+b+c+T\log p)\)，\(T\) 是询问次数 .

放一下代码吧，正好填了前面的坑：

const int N = 3e6 + 10, P = 998244353;
int fac[N], F[N];
inline int qpow(int a, int n)
{
	int ans = 1;
	while (n)
	{
		if (n & 1) ans = 1ll * ans * a % P;
		a = 1ll * a * a % P; n >>= 1;
	} return ans;
}
inline int inv(int x){return qpow(x, P-2);}
int main()
{
	fac[0] = F[0] = 1;
	for (int i=1; i<N; i++) fac[i] = 1ll * fac[i-1] * i % P;
	for (int i=1; i<N; i++) F[i] = 1ll * F[i-1] * fac[i] % P;
	int T, A, B, C; scanf("%d", &T);
	while (T--)
	{
		scanf("%d%d%d", &A, &B, &C);
		if (A > B) swap(A, B);
		if (B > C) swap(B, C);
		if (A > C) swap(A, C);
		if (A + B <= C){printf("%lld 1\n", 4ll * A * B); continue;}
		ll a = A + B - C, b = A + C - B, c = B + C - A;
		printf("%lld %lld\n", 1ll * a * b + 1ll * b * c + 1ll * a * c, 1ll * F[a-1] * F[b-1] % P * F[c-1] % P * F[a+b+c-1] % P * inv(F[a+b-1]) % P * inv(F[b+c-1]) % P * inv(F[a+c-1]) % P);
	}
	return 0;
}