2022.9.30 闲话

Preface

不要管这个叫 Preface 的 H1 .

TOC

目录

• Preface
• 正文
  • 题目描述
  • 题解
    • Subtask 1 & Subtask 2
    • Subtask 3
    • Subtask 4
    • Bonus

呃……

（鼠标）

我的 B 站 20 粉丝了！

\Apjifengc/

……

我在其他网站的粉丝远远是达不到这么多的……

……

……（话题是）我的黑历史！

（背的不对见谅，有部分省略）

---

原文 .

一个普及难度的题，Solution 可以写得多冗长？

Luogu P3909 异或之积

给一个序列 $\{a_n\}$，求

$$6\left(\sum_{i=1}^n\sum_{j=i+1}^n\sum_{k=j+1}^n a_ia_ja_k\right) \bmod (10^9+7)$$

$3\le n\le 10^6$ .

异或搁哪呐？

首先推一波柿子

$$\begin{aligned}6\sum_{i=1}^n\sum_{j=i+1}^n\sum_{k=j+1}^na_ia_ja_k&=6\sum_{i=1}^n\left(a_i\cdot\sum_{j=i+1}^n\sum_{k=j+1}^na_ja_k\right)\\&=6\sum_{i=1}^n\left(a_i\cdot\sum_{j=i+1}^na_j\cdot\sum_{k=j+1}^na_k\right)\end{aligned}$$

记 $\displaystyle S_{l,r}=\sum_{i=l}^ra_i$
则原式就等于

$$6\sum_{i=1}^n\left(a_i\sum_{j=i+1}^na_jS_{j+1,n}\right)$$

先处理出

$$R=\sum\limits_{j=2}^na_jS_{j+1,n}$$

然后 $\Theta(n)$ 暴力算第一个 $\displaystyle\sum$，第二个 $\displaystyle\sum$ 每次求完后将 $R\gets R-a_{i+1}S_{i+2,n}$ 即可 .

时空复杂度 $\Theta(n)$ .

---

伪代码：

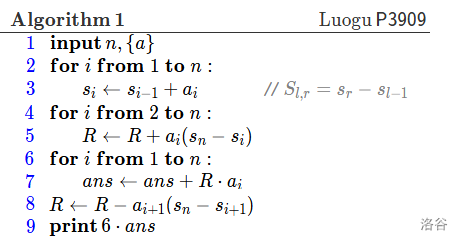
C++ 代码：

using namespace std;
const int N=1e6,MOD=1e9+7;
typedef long long ll;
int n,a[N];
ll S[N],ans,R;
inline __attribute__((always_inline)) ll sum(int l,int r){return ((S[r]-S[l-1])%MOD+MOD)%MOD;}
// 这个 inline __attribute__((always_inline)) 是加速用的，可以忽略 qwq
int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++){scanf("%d",a+i); S[i]=(S[i-1]+a[i])%MOD;}
	for (int i=2;i<=n;i++) R=(R+a[i]*sum(i+1,n)%MOD)%MOD;
	for (int i=1;i<=n;i++){ans=(ans+a[i]*R%MOD)%MOD; R=((R-a[i+1]*sum(i+2,n))%MOD+MOD)%MOD;}
	printf("%lld\n",6*ans%MOD);
	return 0;
}

---

发现以前写的东西还挺好玩的 hszxoj 规则类怪谈，SCP-1919810，？ .

闲话太水也不好，放个题吧，有人说是洛谷上那个叫约数个数和的题弱化版，额好像关系不是很大啊 /youl

好像当时出的时候是根据 3B1B 的感觉出的 .

以下是正文 desu！

正文

题目描述

设

$$x=\prod_{i=1}^{r}p_i^{\alpha_i}$$

其中 $p_i$ 为互不相同的素数，$\alpha_i$ 是大于 $0$ 的整数 .

则令

$$f(x,t)=\prod_{i=1}^r\sum_{j=0}^{\alpha_i}(p_i^j)^t$$

给定 $n,k$，求：

$$\sum_{i=1}^nf(i,k)$$

答案对 $10^9+7$ 取模 .

• Subtask 1 (10 pts)：$1\le n\le 10^4$ .
• Subtask 2 (30 pts)：$1\le n\le 10^5$ .
• Subtask 3 (20 pts)：$1\le n\le 10^6$，$\mu^2(n)=1$.
• Subtask 4 (40 pts)： $1\le n \le 10^6$ .

对于所有数据 $1\le T\le 10$，$1\le n\le 10^6$，$k\in[0,2]$ .

题解

Subtask 1 & Subtask 2

乱搞 / 暴力

Subtask 3

令 $g_p(x)=x^p$，那么推一下这个 $f(n,k)$ 是啥

$$\begin{aligned} \prod_{i=1}^r\sum_{j=0}^{\alpha_i}g_{k}(p_i^j)&=\sum_{i=0}^{\max\{\alpha_i\}}\prod_{j=1}^{r}[\alpha_j\le i]g_{k}(p_j^i)\\&=\sum_{i=0}^{\max\{a_i\}}f_{k}\left(\prod_{j=1}^{r}[\alpha_j\le i]p_j^i\right)\\&=\sum_{d\mid i}g_{k}(d)\\&=\sigma_k(i)\end{aligned}$$

其中 $\sigma_k(n)$ 是 $n$ 的所有约数的 $k$ 次方和 .

所以问题就是要求

$$\sum_{i=1}^n\sigma_k(i)$$

暴力求就可过这一档了 .

Subtask 4

$\sigma_k$ 是积性函数，可以线性筛，然后就可以得到满分了 .

或者写 $O(n\log n)$ 调和级数算法也行 .

Bonus

显然这么经典的问题是有更优做法的 .

众所周知的，有 （$*$ 是狄利克雷卷积）

$$\mu*1=\mathrm{Id}_k$$

$$\sigma_k=1*\mathrm{Id}_k$$

于是，

$$\mu*\sigma_k=\mathrm{Id}_k$$

用杜教筛就可以做出 .

$\mu$ 函数和 $\mathrm{Id}_k$ 的前缀和非常好做，前者杜教筛一下，后者用公式即可 .

时间复杂度大概就是 $\Theta(n^{3/4})$，不知道这里用 $\Theta$ 对不对 .

更优做法我就不会了 .

要是想跑的快快的可以分段打表 .

---

$X$ 是为仅取非负整数值的随机变量，定义其 PGF 为

$$G_X(z)=\mathbb{E}\left(z^X\right)=\sum_{i=0}^{\infty}\operatorname{Pr}(X=i)z^i$$

则有：

1. $G_X(1) = 1$ .
2. $\mathrm E(X^{\underline{k}}) = G_X^{(k)}(1)$ .
3. $\operatorname{Var}(X) = G^{''}_X(1)+G^{'}_{X}(1)-G^{'}_X(1)^2$ .
4. $G_X(z)G_Y(z) = G_{X+Y}(z)$ .