2022.8.21 闲话

今天来一个最炫民族风

最炫民族风

ねぇねぇねぇ。（呐呐呐。） —— ピノキオピー

ねぇねぇねぇ。　＠君へ
呐呐呐。 发送了@你的

一方通行のメンションです
那自说自话的消息

夜明けまで二人　喋っているのに
明明两人直到黎明 都还在聊个不停

ひとりごとみたいな感じ
却还是有着孤单的感觉啊

「チョコレート
「有时候会突然

食べたい時あるよね」
很想吃巧克力啊」

「ノーメイクで可愛い子
「光是素颜就很可爱的人

無敵だね」
简直无敌啊」

「腹立つけどアイツ優しいよね」
「虽然十分不爽 不过那家伙人确实蛮好呢」

ねぇねぇねぇ。　話を聞いてよ
呐呐呐。听我说话啊

目が合わないけど
虽然没有对上视线

「はいはいはい」
“嗯嗯嗯”

興味はないけど
就算兴趣各不相同

「へえ、それで？」
「哦~然后呢？」

笑えないけど
虽然没什么好笑的

「面白いね」
「真有趣啊」

何も感じないけど
即便内心不为所动

「嬉しい」
「好高兴」

聞いてないでしょ
你没在听吧

聞いてないでしょ
你没在听吧

聞いてないでしょ
你没在听吧

知ってるもん
我早就猜到了

こっちの「好き」は
我发过去的「喜欢」

届いてるかな
你真的有收到吗

ねぇねぇねぇ。　＠君へ
呐呐呐。对你发起的@

一方通行のメンションです
只是自言自语的消息

夜明けまで二人　喋っているのに
明明天已微微亮了 两人都还在互发消息

ひとりごとみたいな感じ
却还是感觉若有所失啊

ねぇねぇねぇ。　臆病な劣等生
呐呐呐。胆怯的劣等生

ぼくたちは未経験です
我们仍然懵懂无知呢

世界中　「好き」で溢れてるのに
世界上 明明满溢着“喜欢”的感情

ひとりきりみたいな感じ
却总是觉得内心空荡荡的呢

あなたは今どんな感じ
你现在又是什么感觉呢

「パスコード毎回入力面倒だね」
「每次登录都要重输密码好麻烦的」

「GPS追跡アプリ　便利だね」
「GPS定位的APP 真方便啊」

「今夜は満月が綺麗だね」
「今夜满月的月色真美啊」

ねぇねぇねぇ。　話を聞いてよ
呐呐呐。听我说话呀

わかってないけど
虽然并没有理解

「わかります」
「知道啦」

良く知らないけど
虽然不是很清楚

「ああ、それね」
「啊，你说那个啊」

すべっているけど
虽然一直在别的软件刷个不停

「すべらんなあ」
「没有在刷啊」

ほんとは悲しいけど
即使内心很悲伤

「いぇいいぇい」
「耶耶~」

他愛ない嘘　他愛ない嘘
骗小孩的谎言 骗小孩的谎言

他愛ない嘘　ついてるよ
骗小孩的谎言 不停地在说着

こっちを振り向いて欲しいから
只因想让你看向我这边啊

ねぇねぇねぇ。ハートマーク消して
呐呐呐。删掉爱心的表情

照れ隠しのテンションです
只是想掩饰自己的羞涩啊

ドキドキに蓋をして向かい合う度
每当与你面对面时 都将悸动的心悄悄隐藏

他言語を使ってる感じ
感觉自己都语无伦次了

ねぇねぇねぇ。　端役の八等星
呐呐呐。只配当配角的八等星

不器用なりに夢を見て
傻傻地做着长长的梦

心の奥深くで迷子の恋
于内心深处迷路的爱情

他人事みたいな感じ
感觉和自己毫不相关啊

近いのに遠のいてる感じ
明明近在眼前 却又似远在天边

かまってちゃんって　なんで
你真够缠人的 为什么

身勝手だって　なんで
总是自说自话 为什么

悩んでしまって　不安で
就这样烦恼着 不安着

黙って　泡になっちゃう
沉默着 不小心化作了泡沫

アローン　アローン
Alone Alone

すれ違う双方の
彼此擦肩而过的

ねぇねぇねぇねぇ
呐呐呐呐

無関心も　安心も　紙一重さ
不关心也好 安心也好 也只是一线之隔

ねぇねぇねぇ。　＠君へ
呐呐呐。 发送了@你的

一方通行のメンションです
我自说自话的消息

夜明けまで二人　喋っているのに
明明直到太阳升起 两人都还在聊个不停

ひとりごとみたいな感じ
却还是有着孤单的感觉啊

ねぇねぇねぇ。　臆病な劣等生
呐呐呐。胆怯的劣等生

ぼくたちは未経験です
我们仍然懵懂无知呢

世界中　「好き」で溢れてるのに
世界上 明明满溢着“喜欢”的感情

ひとりきりみたいな感じ
却总是觉得内心空荡荡的呢

あなたは今どんな感じ
你现在是什么感觉呢

二人とも大好きな感じ
是两个人都超喜欢的感觉

片方を選べない感じ
还是难以从两个人抉择的感觉呢

---

IEEE754 浮点数标准

TOC

目录

• IEEE754 浮点数标准
  • 二进制小数与科学计数法
  • 浮点数存储结构
    • IEEE754 存储标准
    • Normalized - 规格化的浮点数
    • Denormalized - 非规格化的浮点数
    • Infinity & NaN - 特殊情况
    • 浮点数分布
    • 示例浮点数
    • 其他类型的浮点数
  • 舍入与精度误差
    • 浮点数精度范围
    • 浮点数舍入
  • Reference

IEEE754 标准链接：https://www.zhihu.com/question/21711083/answer/2388960865 .

IEEE754 创建了一个二进制数到实数的单射（实际上不均匀） .

IEEE754 的初标准在 1985 年发布，也是现在广为流传的版本，被大多数语言所采用 . 事实上后来已经有了更新的标准了，不过两者间没有太大的区别 .

小工具：IEEE754 Converter

二进制小数与科学计数法

初赛我们就学过二进制小数吧，形式大概是这样的：

\[B=\sum_{i=-n}^m2^ib_i \]

早在初中一年级我们就学过科学技术法：\(x=a\cdot 10^n\)，when \(1\le a<10\) .

我们把它变成二进制：\(B=x\cdot 10^y\)，这就是定点数存储方法 .

浮点数存储结构

IEEE754 存储标准

标准提供了四种最常见的规范：

• 单精度 (single) 浮点数 (32bit)
• 双精度 (double) 浮点数 (64bit)
• 延伸单精度 (extended single) 浮点数 (over 43bit)
• 延伸双精度 (extended double) 浮点数 (over 79bit)

IEEE754 规定，浮点数的存储形如

\[value = sign\times exponent\times fraction \]

也就印证了那张经典图：

（值得一提的是，标准中 \(\pm0.0\) 都存在，于是我们做题的时候可能会遇到输出 -0.000000 的情况吧）

CSAPP 里写的标准和此类似：

于是根据 \(s,M,E\)，我们的数可以分为四类：

Normalized - 规格化的浮点数

这是一般情况 .

当 exp 子段不全为 \(0\) 且不全为 \(1\) 时，则浮点数是规格化的 .

在这种情况中，阶码字段被解释为以偏置（biased）形式表示的有符号整数（注意这种表示方法将会在非规格化浮点数中再次提到）.

也就是说，阶码的值是 \(E = e - Bias\)，其中 \(e\) 是无符号数 .

\(e\) 表示为 \(e{k-1}\dots e_1e_0\)，而 \(Bias=2^{k-1}-1\)

小数字段 frac 被解释为描述小数值 \(f\in(0,1)\)，其二进制表示为 \(0.f_{n-1}\dots f_1f_0\)，也就是二进制小数点在最高有效位的左边 .

尾数 \(M\) 定义为 \(M = 1 + f\)，于是我们有时候也说 \(M\) 是 \(1\) 开头的小数，因为根据 \(f\) 的表示，我们可以得到

\[M=1.f_{n-1}\dots f_1f_0 \]

然后因为我们总是能够调整阶码 \(E\)，使得 \(M\in[1,2)\) 之中（假设没有溢出），于是我们可以增加一位精度，因为首位是 \(1\) 不用存 .

Denormalized - 非规格化的浮点数

当 exp 为全 \(0\) 时，所表示的数是非规格化形式 .

此时 \(E=1-Bias\)，\(M=f\) . \(1-Bias\) 便于平滑转变 .

非规格化数有两个用途 .

• 首先,它们提供了一种表示数值 \(0\) 的方法 .
• 非规格化数的另外一个功能是表示那些非常接近于 \(0\) 的数。它们提供了一种属性，称为逐渐溢出 . 其中，可能的数值分布均匀地接近于 \(0.0\) .

（实际上这也导致浮点数分布不均匀）

Infinity & NaN - 特殊情况

注：NaN 是 Not a Number 的意思，也就是不是一个（实）数 .

当指阶码全为 \(1\) 时：

• 当 frac 域全为 \(0\) 时，得到的值表示无穷，符号看 s .
• 否则是 NaN .

可能产生 NaN 的有：

• \(\infty+(-\infty)\) .
• \(0\times\infty\) .
• \(0/0\)，\(\infty / \infty\) .
• 模 \(0\)，被 \(\infty\) 模（为啥浮点数能取模？？？）
• 负数开根号 .

浮点数分布

\([-1,1]\) 的浮点数分布：

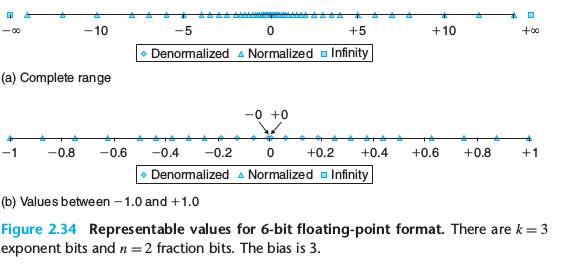
实际上，IEEE754 标准中，\([0,2)\) 里的浮点数比 \([2,\infty)\) 里的浮点数多，可以看 知乎回答 .

示例浮点数

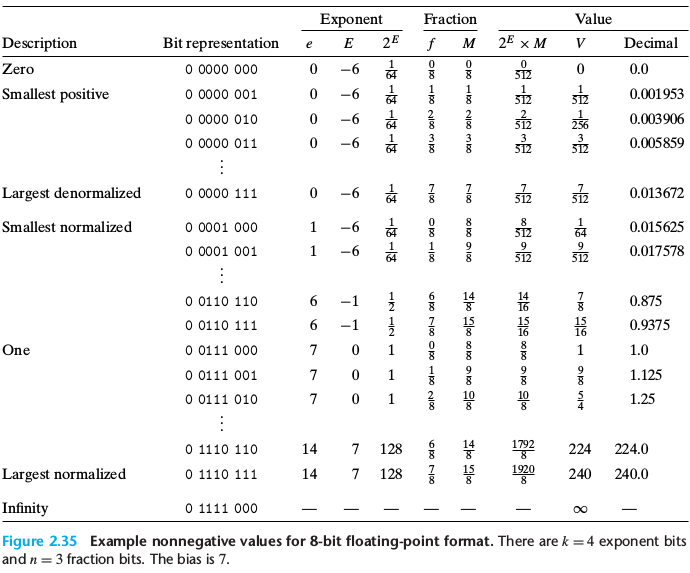
其他类型的浮点数

• 半精度 (Half) 浮点数 (16bit)
  
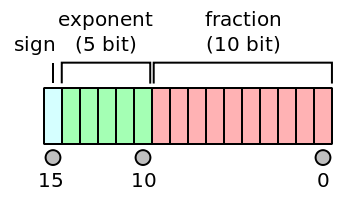
• 四精度 (Quadruple) 浮点数 (128bit)
  
• 八精度 (Octuple) 浮点数 (256bit)
  

延伸精度与上面的又不太一样 .

延伸精度可以视为 精度运算的中间变量，就好像 \(32\) 位整数相乘时，要取到 \(64\) 位一样 .

延伸双精度定为 \(79\) 位以上，便于执行比双精度更精确的计算 . 一些储存标准中为扩展精度提供了专门的最高位 . 按照维基百科最高位的存在使延伸精度可以表示更多 额外状态，比如运算中的精度损失 .

C++ 中 long double 可以实现延伸双精度，长度为 \(80/96/128\) 位 .

舍入与精度误差

浮点数精度范围

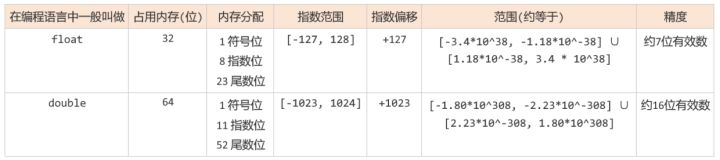
浮点数舍入

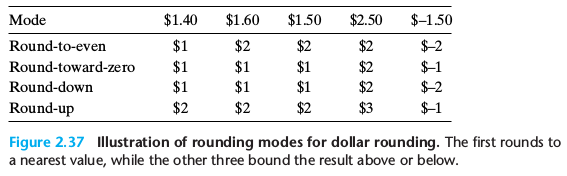
上面是舍入模式的几个例子，相信大家都看懂了 .

C++ 中可以通过 fesetround 调整舍入模式，fegetround 获取舍入模式 .

Reference

• 深入理解计算机系统 / CSAPP
• IEEE 754浮点数标准详解
• IEEE754浮点数表示法——浮点数的范围和误差
• https://www.luogu.com.cn/blog/nederland/