2022.8.2 闲话

UPD. SoyTony 钦定其为钓鱼博 .

《ツギハギスタッカート》

ツギハギだらけの君との时间も

そろそろ终わりにしよう

この糸 ちぎるの

色とりどり 散らばるでしょ

ねぇ ほら あの时の言叶

重ねた 无駄な时间

この糸 ちぎるだけ

不揃いだね 笑えるでしょ

tick tack tick tack 円を描いて

ding dong ding dong あそびましょ

tick tack tick tack 结んで开いて

ding dong ding dong じゃあまたね

解(ほつ)れた糸が嗫く

君よ いっそいっそ いなくなれ

変わらない このままなら

たぶん きっと きっと なんてことない

少し軽くなるだけ

ねぇ いっか いっか 舍てちゃえば

気づかない そのままなら

だけど ずっと ずっと 好きかもな

少しだけ 痛いかな･･･

気づけば気にしてる画面も

そろそろ见饱きた

アレ抜き コレ抜き それじゃ

つまんないんでしょ 退屈でしょ

flick tap flick tap 面を滑って

swipe tap swipe tap 「A.R→T」

flick tap flick tap 开いて 叩いて

swipe swipe swipe swipe もう嫌だな

ズルズル 糸が呟く

君よ いっそ いっそ いなくなれ

変わらない このままだよ

だから きっと きっと なんてことない

少し寂しくなるだけ

もう いっか いっか 舍てちゃえば

気づかない そのままだし

たぶん ずっと ずっと 好きだけど

少しだけ 痛いけど･･･

･･･♪･･･

･･･らんらん･･･

･･･だから･･･

だから いっそ いっそ いなくなれ

変わらない このままだし

たぶん きっと きっと なんてことない

少し寂しくなるけど

ねえ いいの? いいの? 舍てちゃうよ?

気づかない? まだ気づかないなら･･･

･･･そっか そっか 好きなのは･･･

最初から 仆だけ

･･･tick tack tick tack

･･･ding dong ding dong

･･･♪･･･

ツギハギだらけの君との时间を

そろそろ终わりにしよう

この糸 ちぎるだけ

简単でしょ? 笑えるよね?

闲话结束！

\[\Huge\color{red}{\text{WARNING!WARNING!WARNING!}} \]

\[\Huge\color{red}{\text{以下均为瞎扯，请勿当真！}} \]

\[\Huge\color{red}{\text{以下均为瞎扯，请勿当真！}} \]

\[\Huge\color{red}{\text{以下均为瞎扯，请勿当真！}} \]

\[\Huge\color{red}{\text{WARNING!WARNING!WARNING!}} \]

---

对于序列 \(\{a\}\)，令 \(\operatorname{len}(l,r)=r-l+1\)，\(\operatorname{Gmin}_k(l,r)\) 为 \(a_{l\dots r}\) 的 \(k\) 小值，\(\operatorname{Gmax}_k(l,r)\) 为 \(a_{l\dots r}\) 的 \(k\) 大值 .

特别的，\(\min(l,r) = \operatorname{Gmin}_1(l,r)\)，\(\max(l,r) = \operatorname{Gmax}_1(l,r)\)；\(\operatorname{secmin}(l,r) = \operatorname{Gmin}_2(l,r)\)，\(\operatorname{secmax}(l,r) = \operatorname{Gmax}_2(l,r)\).

---

Problem 1

给一个序列 \(\{a\}\)，求

\[\sum_{1\le l\le r\le n}(\max(l,r)-\min(l,r)) \]

答案不超过 64 位无符号整数表示范围 .

首先我们可以拆成最大值和减最小值和，因为答案不超过 64 位无符号整数表示范围，所以直接自然溢出的话答案是对的 .

最大值和最小值本质相同，以最大值为例，这个可以分治，考虑对于一个区间 \([l,r]\)，找出最大值出现位置 \(pos\)，然后分治 \([l,pos)\) 和 \((pos,r]\)，跨过 \(pos\) 的区间的最大值必然都为 \(pos\)，简单统计一下即可 .

ST 表找区间最大值位置，这样是 \(O(n\log n)\) 的 .

我们两遍单调栈找出每个点作为 max 能扩展到的左右端点，大力统计答案即可 \(O(n)\) .

---

Problem 2

给一个序列 \(\{a\}\)，求

\[\sum_{1\le l\le r\le n}\max(l,r)\cdot\min(l,r) \]

答案对 \(2^{64}\) 取模 .

CDQ 分治（烟丝儿飘渺说不算 CDQ 分治），考虑如何维护跨过区间的 max 乘 min，可以双指针扫几遍，\(O(n\log n)\) .

或者线段树扫描线，单调栈维护 max / min，每次 max 和 min 最多改一个（区间长度大于 1），所以可以平凡算贡献，\(O(n\log n)\) .

模数是 \(2^{64}\)，撤操作不能用逆元 .

---

Problem 3

给一个序列 \(\{a\}\)，求

\[\sum_{1\le l\le r\le n}\max(l,r)^{\min(l,r)} \]

答案对 \(10^9+9\) 取模 .

此题已经死了，祝大家万事如意 .

---

Problem 4

给一个序列 \(\{a\}\)，求

\[\sum_{1\le l\le r\le n}\operatorname{rnd}\{\max(l,r),\min(l,r)\} \]

的期望，对 \(10^9+9\) 取模 .

其中 \(\operatorname{rnd}\{A,B\}\) 表示在 \(A,B\) 均匀随机选取一个得到的结果 .

算出所有方案之和然后除以方案数即可 .

方案之和可以简单计算，\(O(n\log n)\) .

---

Problem 5

给一个序列 \(\{a\}\)，求

\[\sum_{1\le l\le r\le n}(\max(l,r)\lor\min(l,r)) \]

答案对 \(10^9+9\) 取模（\(\lor\) 为按位或）.

可以直接大力 CDQ 分治解决，线段树不好维护这个，\(O(n\log n)\) .

---

Problem 6

给一个序列 \(\{a\}\)，求

\[\sum_{1\le l\le r\le n}(\max(l,r)+\min(l,r))^2 \]

答案对 \(10^9+9\) 取模 .

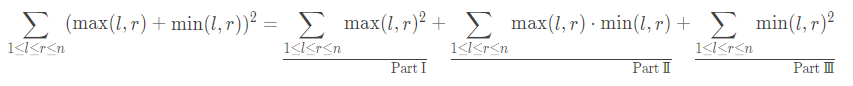
三部分分别维护即可（\(\text{Part I}\) 和 \(\text{Part III}\) 用 Problem 1 类的分治，\(\text{Part II}\) 就是 Problem 2）

时间复杂度 \(O(n\log n)\) .

---

Problem 7

给一个序列 \(\{a\}\)，求

\[\sum_{1\le l\le r\le n}(\operatorname{secmax}(l,r)-\operatorname{secmin}(l,r)) \]

答案不超过 64 位无符号整数表示范围 .

开两个单调栈维护 max 和 secmax，min 同理 .

然后线段树扫描线就行了，\(O(n\log n)\) .

CDQ 分治似乎是要带个 \(2^4\) 的常数 .

---

Problem 8

给一个序列 \(\{a\}\)，求

\[\sum_{1\le l\le r\le n}[\gcd(\max(l,r),\min(l,r))=1] \]

答案对 \(998244353\) 取模 .

SoyTony 做法：枚举一个点 \(i\)，算他和哪些数互素，然后分别算以 \(i\) 为最大值的区间和以那些数为最小值的区间，然后转成区间覆盖解决 .

时间复杂度我不知道 .

---

Problem 9

给一个序列 \(\{a\}\)，求

\[\sum_{1\le l\le r\le n}\lambda(\max(l,r))\lambda(\min(l,r))\lambda(\max(l,r)\cdot \min(l,r)) \]

其中 \(\lambda\) 为刘维尔函数 \(\lambda(x)=(-1)^{\Omega(x)}\)，其中 \(\Omega(x)\) 为 \(x\) 的不同素因数个数 .

答案不超过 64 位无符号整数表示范围 .

因为 \(\lambda\) 是完全积性函数所以原题变成求

\[\sum_{1\le l\le r\le n}\lambda(\max(l,r))^2\lambda(\min(l,r))^2 \]

可以 CDQ 分治解决 /oh/oh/oh

---

Problem 10

给一个序列 \(\{a\}\)，求

\[\sum_{1\le l\le r\le n}\sum_{l\le l'\le r'\le r}\min(l',r')+\max(l',r') \]

答案对 \(998244353\) 取模 .

算一下每个点被多少子区间包含大概就好了，\(O(n^2\log n)\) .

编不下去了……

---

SoyTony's Bonus（改编）

给一个序列 \(\{a\}\)，求

\[\sum_{1\le l\le r\le n}\left(\dfrac{\max(l,r)^{\operatorname{secmin}(l,r)}}{\operatorname{Gmax}_3(l,r)}+\dfrac{\min(l,r)^{\operatorname{secmax}(l,r)}}{\operatorname{Gmin}_3(l,r)}\right)^{f_{typ}(\max(l,r))} \]

• \(typ=1\)：\(f(n)=\mu(n^2)\) .
• \(typ=2\)：\(f(n)=n\) .
• \(typ=3\)：\(f(n)=\varphi(n)\) .
• \(typ=4\)：\(f(n)=\lambda(n)\)（刘维尔函数）.
• \(typ=5\)：\(f(n)=F(n)\) (Fibonacci 数列）.

答案对 \(10^9+7\) 取模 .