2022.7.22 闲话

因为我这莫名其妙上不去 accoders 所以先发个闲话 .

---

Testify

Darkest night, I'll confront you here...

Such a destiny was not desired.

In this place, I never wished to see that side of you.

And raise different colors for one another.

Never notice me.

Never call my name with your voice.

Let me forget everything, still moonlight shines on us.

Broken heart, I don't want you to find and take a look at.

So I'll sin more and destroy my thoughts, make a mess of my hand.

I swear on the darkest night I'll end it all. And testify....

今天我来整个活 .

如有问题请指出 .

idea from Daklqw: link .

浅谈二角函数

目录

• 浅谈二角函数
  • 基本定义
    • 二角形
    • 有向二角形
  • （有向）二角函数的性质
    • 与三角函数的关系
    • 在组合计数中的应用

基本定义

二角形

众所周知，角越少，性质越简单，下面我们开始探讨二角函数（bigonometric function）.

定义二边形为一位数轴上两点 \(A,B\) 组成的图形 \(AB\) 两点构成的封闭图形（\(AB\neq 0\)），易知 \(AB\) 有两个角 \(\angle AB\) 和 \(\angle BA\)，所以二边形也叫二角形（biangle）.

注意这里的 \(\angle AB\) 和 \(\angle BA\) 是任意角，我们钦定一个标准直线（standard line），然后就可以定义它了 .

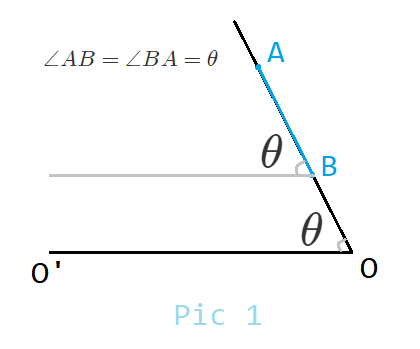
因为一维数轴里无法定义直角，但二角函数对任意二边形都适用，所以我们可以直接定义二角函数 .

\(\large\angle AB=\angle BA=\theta\)

定义二角正弦函数 \(\operatorname{bsin}(\angle AB)=\dfrac{AB}{BA}\) .

类似的，定义二角余弦函数和二角正切函数：\(\operatorname{bcos}(\angle AB)=\dfrac{AB}{BA}\)，\(\operatorname{btan}(\angle AB)=\dfrac{AB}{BA}\) .

它们共称二角弦函数（bigonometric chord function），因为二角弦函数的值都相等，所以我们一般取二角正弦函数 .

类似的，我们可以定义二角割函数（bigonometric secant function）：\(\operatorname{bsec}(\angle AB)=\operatorname{bcsc}(\angle AB)=\operatorname{bcot}(\angle AB)=\dfrac{BA}{AB}\) .

类似的，可以定义它们的反函数，\(\operatorname{barcsin},\operatorname{barccos},\operatorname{barctan},\cdots\) .

这样，几何意义和代数意义均鲜明的二角函数便被创造出来了 .

有向二角形

我们把二角形的边定向，则可以定义有向二角形（directed biangle），同时也可以定义有向二角函数（directed bigonometric function），如 \(\operatorname{dbsin}(\alpha)\) .

有向二边形里的有向边是包含方向的，类似于向量 .

（定义： \(\operatorname{dbsin}(\angle AB)=\dfrac{\overrightarrow{AB}}{\overrightarrow{BA}}\)，\(\operatorname{dbcos},\operatorname{dbtan}\) 等一样）

这样我们就定义完了二角函数及有向二角函数 .

（有向）二角函数的性质

这里先定义一个特殊函数：\(\displaystyle \operatorname{gbexp}_k(x)=x^{-k}\int_{2x^k/3}^{x^k}(\operatorname{dbsin}^k(z)-\operatorname{bcos}^k(z)+\operatorname{dbtan}^k(z))\mathrm dz\)，其中上标表示函数复合 .

特别的，\(\operatorname{bexp}(x)=\operatorname{gbexp}_x(x)\)（\(x\in\mathbb N_+\)）.

与三角函数的关系

不难发现，有如下恒等式成立：

\[\begin{aligned}\sin(\alpha)&=\sum_{k\ge 1}\operatorname{bexp}(k-1)\dfrac{\alpha^{2k-1}}{(2k-1)!}\\\cos(\alpha)&=\sum_{k\ge 1}\operatorname{bexp}(k)\dfrac{\alpha^{2k}}{(2k)!}\end{aligned} \]

有了 \(\sin\) 和 \(\cos\)，一切的三角函数就都可以表示了 .

甚至你还可以说这个是 EGF 形式

在组合计数中的应用

称作有向二角函数反演理论（directed bigonometric function inversion theory）.

此文 中提到了一份应用 \(\operatorname{bsin}\) 函数求解错排数问题的

下面放一些简单的有向二角函数反演内容 .

bcf 斯特林容斥：

\[x^n=\sum_{i=0}^n\sum_{j=0}^i{n\brace i}{i\brack j}\operatorname{bexp}(i-j)x^j \]

bcf 子集反演：

\[f(S)=\sum_{T\subseteq S}g(T)\Longleftrightarrow g(S)=\sum_{T\subseteq S}\operatorname{bexp}(|S|-|T|)f(T) \]

bcf 数论对数容斥：

\[\operatorname{lcm}(T)=\exp\left(\sum_{S\subseteq T,S\neq\varnothing}\operatorname{bexp}(|S|+1)\cdot\ln(\gcd(S))\right) \]

---

一个有意思的内容：

bsc 整除性反演：

\[[n\mid a]=\dfrac1n\sum_{i=0}^{n-1}\left(\left(\sum_{k\ge 1}\operatorname{bexp}(k)\pi^{2k}\cdot \dfrac{2^{2k}i^{2k}}{n^{2k}(2k)!}\right)+\left(\sum_{k\ge 1}\operatorname{bexp}(k)\pi^{2k-1}\cdot \dfrac{2^{2k-1}i^{2k-1}}{n^{2k-1}(2k-1)!}\right)\mathrm i\right) \]

证明繁而不难，略去 .

令 \(\displaystyle f(n,i)=\left(\sum_{k\ge 1}\operatorname{bexp}(k)\pi^{2k}\cdot \dfrac{2^{2k}i^{2k}}{n^{2k}(2k)!}\right)+\left(\sum_{k\ge 1}\operatorname{bexp}(k)\pi^{2k-1}\cdot \dfrac{2^{2k-1}i^{2k-1}}{n^{2k-1}(2k-1)!}\right)\mathrm i\)，则可以得到 \(f(n,k)=f(n,n+k)\) 且 \(|f(n,k)|=1\).

于是 \(f\) 具有周期性，可以快速解决某些问题 .

例题：

给一个序列 \(\{a\}\) 和一个常数 \(s\)，求：

\[\sum_{i=0}^n\dbinom nis^ia_{i\bmod 4} \]

对 \(998244353\) 取模 .

把 \(a_{i\bmod 4}\) 拆成 \(\displaystyle\sum_{k\in[0,4)}a_k[k\equiv i\pmod4]\) 即可（同余可以简单化为整除）.

后面就是 bsc 整除性反演的样子了，略去 .

---

一个有挑战性的内容：

bsc 偏序反演：

对于任意偏序 \(\preceq\)，定义 bsc 奥妙函数为

\[\operatorname{bao}(x,y)=\begin{cases}1&x=y\\\displaystyle\operatorname{dbsin}(x^2+y^2)\sum_{x\preceq z\prec y}\operatorname{bao}(x,z)&x\prec y\end{cases} \]

则有：

\[g(x)=\sum_{y\preceq x}f(y)\Longleftrightarrow f(x)=\sum_{y\preceq x}g(y)\operatorname{bao}(x,y) \]

它的一个特例就是 Mobius 反演 .

---

后面不想写了，