来自学长的馈赠1 社论

Alice

注意到一奇一偶的情况只能变成俩奇数，于是对面再给变回一奇一偶, 直到有一个为 $0$ 就可以赢了 .

于是一奇一偶必胜，两奇必败，两偶数的同时除以几个 $2$ 即可，容易证明除因子不影响答案 .

Box

假设没有停止这个东西，可以一直取 . 设取完第 $i$ 种颜色的球的次数为 $X_i$，则答案就是 $X=\min\{X_i\}$ .

min-max 容斥，则

$$\mathbb E(X)=\sum_{T\subseteq X\land T\neq\varnothing}(-1)^{|T|-1}\mathbb E(\max\{T\})$$

根据神秘组合意义可以得到当 $|T|=x$ 时 $\displaystyle\max\{T\}=mx + \dfrac{mx}{mx+1}\cdot m(n-x)$ .

于是把 $|T|$ 相等的写在一起，即得

$$\mathbb E(X)=\sum_{i=1}^n(-1)^{i-1}\dbinom ni\left(mi + \dfrac{mi}{mi+1}\cdot m(n-i)\right)$$

可以 $O(n\log n)$ 算，然而会超时 .

可以把逆元提出来最后算，这样就可以过了 .

或者说只会有 $O(n)$ 个本质不同的 $mi+1$ 作为分母，考虑使用线性求任意 $n$ 个数的逆元之 Trick 即可 .

Common

Algorithm 1

不强于 2D - 2SUM 问题 .

首先定义 $\operatorname{encode}(a, b) = 4001a + b$ .

令 $\displaystyle t_k=\sum_{i=1}^n[\operatorname{encode}(a_i, b_j)=k]$，构造多项式：

$$F(z)=\sum_{k\ge 0}z^kt_k$$

于是考察卷积 $G=F^2$，则不难发现 $\displaystyle G(\operatorname{encode}(x,y))=\sum_{1\le i,j\le n}[b_i+b_j=x][c_i+c_j=y]$ .

那么我们暴力枚举一波 $x,y$，答案就可以算了：

$$\begin{aligned}ans&=\sum_{1\le x,y\le n}a_{x,y}\sum_{1\le i,j\le n}[b_i+b_j=x][c_i+c_j=y]\\&=\sum_{1\le x,y\le n}a_{x,y}\cdot G(\operatorname{encode}(x,y))\end{aligned}$$

注意到模数是 $998244353$，于是可以一次 NTT $O(m^2\log m)$ 求 $G$，别的操作都不超过 $O(m^2)$ .

总复杂度 $O(m^2\log m)$，常数非常大，跑不进 2s TAT .

Algorithm 2

注意到 $a$ 矩阵是由递推形式给出 .

于是可以在 $a$ 上操作，相当于 $\Theta(n^2)$ 次操作一起做 .

具体的，对于每个 $i$，在 $(-b_i,-c_i)$ 上加一，递推后在 $(b_i,c_i)$ 处统计答案即可 .

负下标可以平移解决 .

Do not ak

题目链接 .

没学过分块.psd

开摆！

---

UPD. 我还是补补吧 😃

UPD. Give up.

UPD. Never Gonna Give You Up!!!

---

时间复杂度 $O(f(x))$ 空间复杂度 $O(g(x))$ 记 $O(f(x))-O(g(x))$ .

Tip. 统计两个有序数组间产生的逆序对个数可以归并（即归并排序的合并两数组部分） .

首先分块，块长设为 $B$ .

那么就有两种情况：

Case 1 左右端点 $l,r$ 不在同一块内 .

考虑一下逆序对贡献的产生：

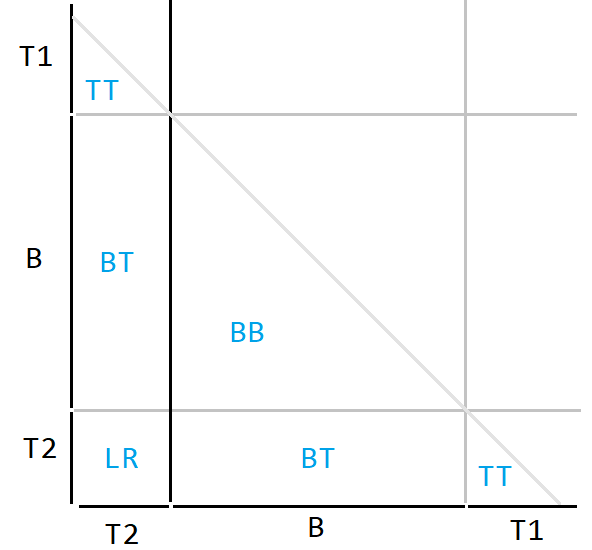
如图，$T_1,T_2$ 是左右散块，$B$ 是若干整块，于是就有贡献：

• TT：散块自己内部贡献 .
• BB：整块自己内部贡献 .
• BT：散块对整块贡献 .
• LR：散块间贡献 .

对于 TT，我们处理一个 $pre_i,suf_i$，表示 $i$ 到其所在块左端点 / 右端点的逆序对贡献，这个可以权值树状数组扫一遍得到 .

这样就可以直接干了，总复杂度 $O(n\log n) - O(n)$ .

对于 BT，我们只需要对于左侧散块的每个数 $x$，统计中间有多少个数 $\le x$；对于右侧散块每个数 $x$，统计中间有多少个数 $\ge x$ .

这个可以 $O(n^2/B) - O(n^2/B)$ 预处理前缀和 .

对于 LR，块内排序，直接归并即可，$O(B) - O(1)$ .

对于 BB，考虑预处理出所有答案 .

双指针，设目前左右端块为 $l,r$，则直接加上以前有的贡献，再枚举块内元素 $x$，用以前维护过的东西求出前面若干块内 $\ge x$ 即可 .

复杂度 $O(nB) - O(B^2)$ .

Case 2 左右端点 $l,r$ 在同一块内 .

拆成两个前缀逆序对之差和块间逆序对，前者预处理，后者归并 .

于是 $O(B)-O(n)$ .

取 $B = \sqrt n$ 得最优复杂度 $O(n\sqrt n)-O(n\sqrt n)$ .

Code

using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
constexpr int N = 1e5 + 7, B = 514;
int n, q, a[N], pre[N], suf[N], buc[N], c[N], lt[B][N], bl[B][B];
int bs, bcnt, L[B], R[B], bel[N];
pii b[B][B];
struct FenwickTree
{
	int f[N];
	static inline int lowbit(int x){return x & -x;}
	inline void clear(){memset(f, 0, sizeof f);}
	inline void add(int x, int a){for (int i=x; i<=n; i+=lowbit(i)) f[i] += a;}
	inline int query(int x)const{int ans = 0; for (int i=x; i; i&=i-1) ans += f[i]; return ans;}
}F;
inline void init()
{
	for (int i=1; i<=bcnt; i++)
	{
		L[i] = (i-1) * bs + 1; R[i] = min(i*bs, n);
		for (int j=L[i]; j<=R[i]; j++) bel[j] = i;
	}
	for (int i=1; i<=n; i++) b[bel[i]][i-L[bel[i]]+1] = make_pair(a[i], i);
	for (int i=1; i<=bcnt; i++) stable_sort(b[i]+1, b[i]+R[i]-L[i]+2);
	for (int i=1; i<=bcnt; i++)
	{
		F.clear(); ll sum = 0;
		for (int j=L[i]; j<=R[i]; j++){pre[j] = (sum += j - L[i] - F.query(a[j])); F.add(a[j], 1);}
		F.clear(); sum = 0;
		for (int j=R[i]; j>=L[i]; j--){suf[j] = (sum += F.query(a[j])); F.add(a[j], 1);}
	}
	for (int i=1; i<=bcnt; i++)
	{
		int minn = n+1, s = 0;
		for (int j=L[i]; j<=R[i]; j++){++c[a[j]]; chkmin(minn, a[j]);}
		for (int j=minn; j<=n; j++){s += c[j]; buc[j] += s;}
		for (int j=L[i]; j<=R[i]; j++) --c[a[j]];
		for (int j=1; j<=n; j++) lt[i][j] = buc[a[j]-1];
	}
	for (int i=1; i<=bcnt; i++)
		for (int j=1; j<i; j++)
			for (int k=L[i]; k<=R[i]; k++) bl[i][j] += R[j] - lt[j][k];
}
inline ll query(int l, int r)
{
	if ((l<1) || (r<1) || (l>n) || (r>n) || (l>r)) return 0;
	if (bel[l] == bel[r])
	{
		ll ans = pre[r];
		int le = L[bel[l]], ri = R[bel[l]];
		if (l != le) ans -= pre[l-1];
		for (int i=1, c=0; i<=ri-le+1; i++)
		{
			int _ = b[bel[l]][i].second; 
			if (_ < l) ans -= c;
			c += ((l <= _) && (_ <= r));
		} return ans;
	}
	ll ans = suf[l] + pre[r];
	int lb = bel[l], rb = bel[r], le = L[lb], ri = R[rb];
	for (int i=lb+1; i<rb; i++) ans += pre[R[i]] + bl[i][i-1] - bl[i][lb]; // 整块间
	for (int i=l; i<=R[lb]; i++) ans += lt[rb-1][i] - lt[lb][i];
	for (int i=L[rb]; i<=r; i++) ans += L[rb] - R[lb] - 1 - (lt[rb-1][i] - lt[lb][i]); 
	for (int i=1, j=1, c=0; i<=R[lb]-le+1; i++)
	{
		while ((j <= ri - L[rb] + 1) && (b[rb][j].first < b[lb][i].first)){c += (b[rb][j].second <= r); ++j;}
		if (b[lb][i].second >= l) ans += c;
	}
	return ans; 
}
int main()
{
	scanf("%d%d", &n, &q);
	bs = 300; bcnt = (n-1) / bs + 1;
	for (int i=1; i<=n; i++) scanf("%d", a+i);
	init();
	int l, r; ll lstans = 0;
	while (q--)
	{
		scanf("%d%d", &l, &r); l ^= lstans; r ^= lstans;
		printf("%lld\n", lstans = query(l, r)); 
	} return 0;
}