2022 暑假 🐍🐋

Updating ...

7.20

二维凸包

定义就不说了

Andrew 算法

按照 $x$ 坐标为第一关键字，$y$ 坐标为第二关键字从小到大排序 .

从第一个点开始，如果下一个点在栈顶的两元素所连成直线的左侧就入栈（用叉积简单判断），如果在右侧，则栈顶元素出栈，并继续判断栈顶的两个新元素与下一个点的关系，这样到最后得到的是上半个凸包，只需要再倒序来一遍，便可以求出下凸包 .

Andrew 算法

using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int, int> pii;
const int N = 114514;
const db INF = 1e12;
int n;
struct point{db x, y; point(db a=0, db b=0) : x(a), y(b){}}p[N];
template<typename T>
inline T sqr(const T& x){return x * x;}
inline db dist(const point& a, const point& b){return sqrt(sqr(a.x - b.x) + sqr(a.y - b.y));}
inline db slope(const point& a, const point& b){return a.x == b.x ? INF : (a.y - b.y) / (a.x - b.x);}
int st[N], top;
int main()
{
	scanf("%d", &n);
	for (int i=1; i<=n; i++) scanf("%lf%lf", &p[i].x, &p[i].y);
	stable_sort(p+1, p+1+n, [&](point a, point b){return (a.x == b.x) ? (a.y < b.y) : (a.x < b.x);});
	db ans = 0;
	for (int i=1; i<=n; i++)
	{
		st[++top] = i;
		while ((top > 2) && (slope(p[st[top]], p[st[top - 2]]) < slope(p[st[top - 1]], p[st[top - 2]]))){st[top - 1] = st[top]; --top;} 
	}
	for (int i=1; i<top; i++) ans += dist(p[st[i]], p[st[i+1]]);
	top = 0;
	for (int i=n; i>=1; i--)
	{
		st[++top] = i;
		while ((top > 2) && (slope(p[st[top]], p[st[top - 2]]) < slope(p[st[top - 1]], p[st[top - 2]]))){st[top - 1] = st[top]; --top;} 
	}
	for (int i=1; i<top; i++) ans += dist(p[st[i]], p[st[i+1]]);
	printf("%.2f\n", ans); // ans ==> 凸包周长
	return 0;
}

动态凸包

操作：

加点
询问一个点 $(x,y)$ 是否在凸包内 .

也是 Andrew 算法的思路 .

用两个 std :: map 分别维护上下凸壳，加点的时候如果不在凸包内就尝试用其尝试删除其相邻的点，并不断删除至无法删除为止（用叉积简单判断），每个点只会最多被删除一次，故复杂度正确 .

CF70D Professor's task

using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int, int> pii;
const int N = 114514;
inline ll det(const int& a, const int& b, const int& c, const int& d){return 1ll * a * d - 1ll * b * c;}
struct DCH // Dymanic Convex Hull, from EI
{
	template<typename op>
	struct UD_DCH
	{
		map<int, int> M;
		inline bool check(int x, int y)
		{
			auto it = M.lower_bound(x);
			if (it == M.end()) return false;
			if (it -> first == x) return op()(y, it -> second);
			if (it == M.begin())  return false;
			auto jt = it; --jt;
			return op()(det(it->first - jt->first, it->second - jt->second, x - jt->first, y - jt->second), 0); 
		}
		inline bool remove(std :: map<int, int> :: iterator it)
		{
			if (it == M.begin()) return false;
			auto jt = it, kt = it; --jt; ++kt; 
			if (kt == M.end()) return false;
			if (!op()(det(it->first - jt->first, it->second - jt->second, kt->first - jt->first, kt->second - jt->second), 0)){M.erase(it); return true;}
			return false;
		}
		inline void insert(int x, int y)
		{
			if (check(x, y)) return ;
			M[x] = y;
			auto it = M.find(x); auto jt = it;
			if (it != M.begin())
			{
				--jt;
				while (remove(jt++)) --jt;
			}
			if (++jt != M.end()) while (remove(jt--)) ++jt;
		}
	};
	UD_DCH<greater_equal<ll> > top; UD_DCH<less_equal<ll> > down;
	inline void insert(int x, int y){top.insert(x, y); down.insert(x, y);}
	inline bool check(int x, int y){return top.check(x, y) && down.check(x, y);}
}D;

树的直径与重心

树的直径

定义：~~树中离得最远的两个点之间的路径~~ 树上的最长简单路径 .

求法：

两次 BFS / DFS：先从任意一点 $P$ 出发，找离它最远的点 $Q$，再从点 $Q$ 出发，找离它最远的点 $W$，$W$ 到 $Q$ 就是直径 .
树形 DP：一条直径可以拆成两条直链拼起来，于是维护子树直链最大值 & 次大值即可，这个可以 DP 简单维护 .

性质：

直径两端点必是叶子 .
某个距离任意点最远的点一定是某个直径的一个端点 .
两棵树 $\mathcal T_1,\mathcal T_2$ 的直径分别是 $u\leftrightarrow v$，$x\leftrightarrow y$，则用一条边将两棵树连接后，新直径的端点必然在 $\{u,v,x,y\}$ 中 .
（3 推论）一棵树加一个节点接叶子上，直径端点最多变化一个 .
所有直径中点相同 .

树的重心

定义：节点数最大子树的节点数最小的点

求法：

可以一次 DFS 得到子树 & 子树补信息，然后暴力判即可 .
从某个点开始，向节点数超过整棵树节点数的一半的方向走，若其所有儿子的节点数均小于等于其整棵树节点数的一半，那么该节点为树的重心 .

性质：

一棵树最多有两个重心，若有则相邻 .
只有以重心为根，每个子树的大小才不会超过总点数一半 .
把两个树通过一条边相连得到新树的重心在原来两个树的重心之间的简单路径上 .
（3 推论）把一个树添加或删除一个叶子，那么它的重心最多移动 1 .
树中所有点到某个点距离和中，到重心距离和是最小的

cdq 分治

简要思想

对于一个东西，分两份分治考虑：

左边自己的贡献 .
右边自己的贡献 .
左右之间的贡献 .

三维偏序

陌上花开

$n$ 个三元组 $(a_i,b_i,c_i)$，令 $ f(i) $ 表示满足 $ a_j \leq a_i $ 且 $ b_j \leq b_i $ 且 $ c_j \leq c_i $ 且 $ j \ne i $ 的 $j$ 的数量 .

对于 $d \in [0, n)$，求 $f(i) = d$ 的数量 .

首先第一维排序，然后对它 cdq 分治 .

左右分别排序，双指针 + 树状数组即可处理左右信息的合并 .

时间复杂度 $O(n\log^2 n)$ .

优化 DP

Building Bridges

有 $n$ 根柱子依次排列，每根柱子都有一个高度。第 $i$ 根柱子的高度为 $h_i$ .

现在想要建造若干座桥，如果一座桥架在第 $i$ 根柱子和第 $j$ 根柱子之间，那么需要 $(h_i-h_j)^2$ 的代价 .

在造桥前，所有用不到的柱子都会被拆除，因为他们会干扰造桥进程。第 $i$ 根柱子被拆除的代价为 $w_i$，注意 $w_i$ 不一定非负，因为可能政府希望拆除某些柱子 .

现在政府想要知道，通过桥梁把第 $1$ 根柱子和第 $n$ 根柱子连接的最小代价 . 注意桥梁不能在端点以外的任何地方相交 .

令 $\{s\}$ 为 $\{w\}$ 的前缀和 .

令 $dp_i$ 为把第 $1$ 根柱子和第 $i$ 根柱子连接的最小代价，转移：

\[dp_i=\min_{j<i}\{dp_j+(h_i-h_j)^2+s_{i-1}-s_j\} \]

斜率优化的形式，但是两维都不单调 .

常见处理方法就是动态凸包（平衡树），cdq 分治或李超线段树 .

我们对下标 cdq 分治，于是只需要处理左边对右边的转移，左边建出凸包后，右边既可以排序也可以直接在凸包上二分 .

时间复杂度 $O(n\log^2 n)$ .

对时间维分治

维护一个数据结构，支持矩形加，矩形求和 .

假做法：二维线段树 / 四分树（单次最坏 $O(n))$）

真做法：树套树 .

考虑离线后对时间维做 cdq 分治，那么我们只需要处理两侧之间的贡献 .

观察可以发现，只有左侧的修改对右侧的询问有贡献，于是可以扫描线 .

时间复杂度 $O(n\log^2 n)$ .

虚树

省流：

树上问题，求一堆关键点间的信息 .

只需要留下关键点及其 LCA 即可 .

维护时只需维护一条右链，具体见 OI Wiki .

一个例子是 HEOI2014 大工程 .

7.22

快速乘：

\[a\cdot b\bmod p = \left(a-p\left\lfloor\dfrac{ab}p\right\rfloor\right)\bmod p \]

除可以 long double 算，因为 $p<2^{64}$ 所以后面直接 unsigned long long 自然溢出即可 .

BSGS

解关于 $x$ 的方程：

\[a^x\equiv b\pmod p \]

其中 $p$ 是素数 .

大概就是以 $\sqrt p$ 为块长分块然后块内块间直接暴力，类似光速幂吧 .

注意做 $q$ 次 BSGS 的时间复杂度是 $O(\sqrt{pq})$，$p$ 是模数 .

BSGS

unordered_map<int, int> H;
inline int BSGS(int p, int b, int n)
{
	if (!(b%p)) return -1;
	int m = sqrt(p) + 1, base = n % p;
	for (int i=0; i<=m; i++, base = 1ll * base * b % p) H[base] = i;
	base = qpow(b, m, p);
	int tmp = 1;
	for (int i=1; i<=m; i++){tmp = 1ll * tmp * base % p; if (H[tmp]) return ((1ll * i * m - H[tmp]) % p + p) % p;}
	return -1; 
}

矩阵的这样的高次同余方程也能这么整 .

整体二分

决策单调性

7.25

线性基

定义与构建

异或向量空间的一组基 .

构造：按位扫一遍 .

合并可以暴力合，也可以启发式合，但是一般来说要合的线性基大小都是一样的所以不用启发式合 .

线性基 Linear Basis

struct basis
{
public: 
	inline void reset(){memset(t, 0, sizeof t);}
	inline void insert(ll x)
	{
		for (int i=B-1; i>=0; i--)
		{
			if (!(x >> i & 1)) continue;
			if (!t[i]){t[i] = x; return ;}
			x ^= t[i];
		}
	}
	inline basis& operator += (const basis& rhs)
	{
		for (int i=0; i<B; i++)
			if (rhs[i]) this -> insert(rhs[i]);
		return *this;
	}
	inline basis operator + (const basis& rhs)const{basis _ = *this; _ += rhs; return _;}
	inline basis& operator = (const basis& rhs){for (int i=0; i<B; i++) t[i] = rhs[i]; return *this;}
	basis(){reset();}
	~basis() = default;
protected:
	static const int B = 63;
	ll t[B];
	inline ll operator [](const unsigned& id)const{return t[id];}
	inline ll& operator [](const unsigned& id){return t[id];}
	friend ll maxxor(const basis&);
};

经典问题

最大子集异或和

给一个集合 $S$，求一个集合 $T\subseteq S$ 使得 $\operatorname{xor}(T)=\displaystyle\bigoplus_{k\in T}k$ 最大 .

线性基按位从高到低扫一遍更新答案 .

正确性来自字典序贪心 .

最小子集异或和

给一个集合 $S$，求一个集合 $T\subseteq S \land T\neq\varnothing$ 使得 $\operatorname{xor}(T)=\displaystyle\bigoplus_{k\in T}k$ 最小 .

线性基中最小元素 .

kth 子集异或和

给一个集合 $S$，有一个集合 $T\subseteq S \land T\neq\varnothing$，求第 $k$ 大的 $\operatorname{xor}(T)=\displaystyle\bigoplus_{k\in T}k$ .

子集异或方案数

给一个集合 $S$ 和一个数 $x$，问有多少个集合 $T\subseteq S \land T\neq\varnothing$ 使得 $\operatorname{xor}(T)=\displaystyle\bigoplus_{k\in T}k=x$ .

根据 pl_er 定理我们知道方案数是均分的，于是我们只需要判断是否可以异或出来 .

类似插入，如果最后变成 0 了就说明能异或出来 .

动态线性基

给一个集合 $S$，支持插入删除元素，每次求一个集合 $T\subseteq S$ 使得 $\operatorname{xor}(T)=\displaystyle\bigoplus_{k\in T}k$ 最大 .

树上线性基

给一棵树 $\mathcal T$，多组询问，每次询问令 $u$ 到 $v$ 简单路径上的所有点权组成集合 $S$，求一个集合 $T\subseteq S$ 使得 $\operatorname{xor}(T)=\displaystyle\bigoplus_{k\in T}k$ 最大 .

类似倍增 LCA，倍增的处理 $t_{i,j}$ 表示 $i$ 往上跳 $2^j$ 步的线性基 .

线性基合并直接暴力即可，下面的 log 不计线性基合并复杂度 .

如果爆拆（LCA 做法）是 3log，类似 ST 表的合并方法是 2log，点分治可以 1log .

基环树

NOIP2018 提高组旅行

枚举每条边删了贪心 .

Hobson 的火车

树的情况就是子树内深度不大于 $k$ 的数个数，分块 $\Theta(n\sqrt{n\log n})$ 持久化线段树 $\Theta(n\log n)$，树上差分那个不知道咋做的 .

变成基环树考虑断一条边然后算边对每个点的贡献即可 .

时间复杂度 $\Theta(n\log n)$ .

创世纪 / 骑士 / 城市环路（基环树（带权）最大独立集）

考虑先对环的所有子树 DP，然后在环上 DP 拼起来 .

或者断一条边 DP，然后在边上算一下 .

时间复杂度 $\Theta(n)$ .

约会 Rendezvous

基环树 LCA

环缩起来考虑即可 .

基环树直径

处理前后缀答案环上每条边断一下算答案 .

有标号基环树计数

有根树的 EGF：$\displaystyle F(z)=\sum_{k\ge 0}k^{k-1}\dfrac{z^k}{k!}$ .

答案的 EGF：

\[G(z) =\frac{1}{2}\sum_{k\ge 1} \frac{F^k(z)}{k!}=-\dfrac{\ln(1-F(z))}2 \]

除以二是环正反两种情况 .

Urban Planning

问题可以转换成计数连通块数量 .

假设连完后一个环上有 $k$ 个内向树，大小分别为 $a_{1\dots k}$，则方案就是圆排列，即为

\[\displaystyle (k - 1)! \prod_{i = 1}^{k} a_i \]

特判 $k=1$ .

于是依次加入内向树 DP 即可 .

信息传递

基环树环长 .

直接 DFS .

带修信息传递（每次改父亲）

ETT 状物 .

Island

占位

Catalan 数

球迷购票问题 .
不穿过对角线的格路计数 .
原上选 $2n$ 个点两两连线不交方案数 .
凸多边形三角剖分方案数 .
出栈序列方案数 .
二叉树个数 .
$\pm1$ 构成的序列中部分和恒大于零的方案数 .

Catalan 数：1, 1, 2, 5, 14, 42, 132，……

Catalan 数公式：

\[C_n=\dfrac1{n+1}\dbinom{2n}n \]

\[C_n=\dbinom{2n}n-\dbinom{2n}{n-1} \]

\[C_n=\sum_{i=1}^nC_{i-1}C_{n-i} \]

\[C_n=\dfrac{C_{n-1}(4n-2)}{n+1} \]

wqs 二分

7.26

可持久化数据结构

数位 DP

$k$-D Tree

点分治

7.27

圆方树

AC 自动机

见 AC 自动机 .

01 分数规划

李超线段树

7.29

Manacher

manacher 算法可以求字符串的所有回文串 .

显然我们只需要算最长回文半径即可，首先把任意相邻两字符直接随便插一个字符，这样就只需要考虑奇回文了 .

我们观察两回文串相交时的情况大概就可以转移了，$O(n)$（具体看 SoyTony 的博客）.

Manacher

// 最长回文子串
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 1.1e7;
int n, d[N << 1], ans = 1;
string s = "$", t;
int main()
{
	cin >> t; n = t.length();
	for (char ch : t){s.push_back('?'); s.push_back(ch);}
	s.push_back('?'); n = (n << 1) + 1;
	for (int i=1,l=0,r=-1,j,k; i<=n; i++)
	{
		j = l+r-i;
		k = ((i > r) ? 1 : min(d[j], r-i+1));
		while ((i-k >= 1) && (i+k <= n) && (s[i-k] == s[i+k])) ++k;
		d[i] = k;
		chkmax(ans, d[i]/2*2 - (i&1^1));
		if (i+k-1 > r){l = i-k+1; r = i+k-1;}
	} printf("%d\n", ans);
	return 0;
}

魔改 Manacher：

双倍回文

字符串 $s$ 的倒置记作 $s^{\sf R}$ .

形如 $ww^{\mathsf R}ww^{\mathsf R}$ 的串被称为双倍回文串 .

给一个字符串，求最长双倍回文子串 .

维护一波 $ww^{\mathsf R}ww^{\mathsf R}$ 的回文半径即可 .

Antisymmetry

对于一个 01 串，如果取反（1 变成 0，0 变成 1）再翻转后和原串一样，就称作反对称字符串 .

给一个 01 串，求反对称子串个数 .

重定义一下回文就好了 .

Manacher 题大概 PAM 都能做吧 .

回文自动机 / 回文树

定义与构建

建两棵树，一棵树中的节点对应的回文子串长度均为奇数，另一棵树中的节点对应的回文子串长度均为偶数（奇根偶根） .

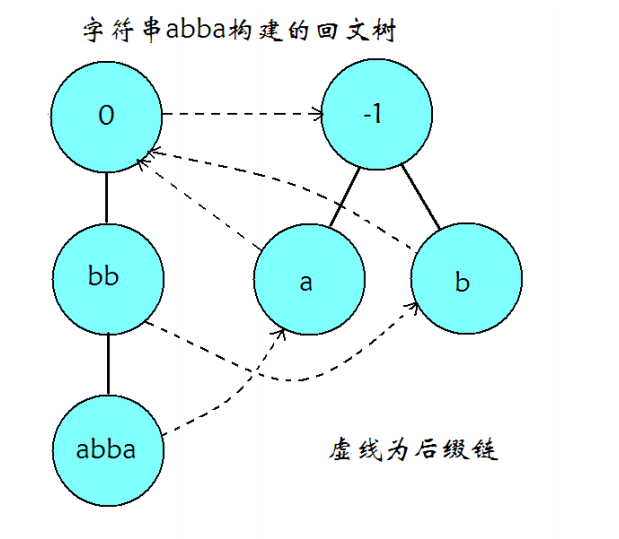
一个节点的 fail 指针指向的是这个节点所代表的回文串的最长回文后缀所对应的节点，转移边表示在原节点代表的回文串前后各加一个相同的字符（因为要保证回文）.

每个节点顺便记一下字符串长度，方便算 .

PAM 构造就是考虑增量构造 .

考虑构造完前 $p$ 个字符的回文树后，向自动机中添加在原串里位置为 $p+1$ 的字符。

我们从以上一个字符结尾的最长回文子串对应的节点开始，不断沿着 fail 指针走，直到找到一个节点满足 $s_p=s_{p-len-1}$，即满足此节点所对应回文子串的上一个字符与待添加字符相同，就可以连边了 .

大概就是：

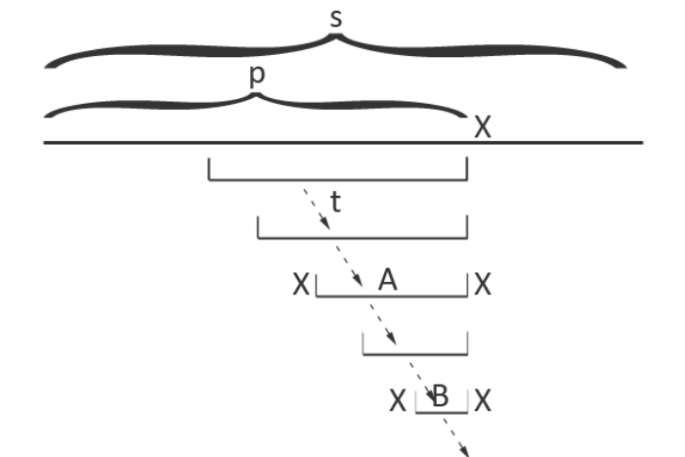
注意要先赋 fail 指针的值要不然有可能会错~~（具体问 Su_Zipei）~~ .

PAM

struct PAM
{
	static const int alphabet = 26;
	int sz, cc, lst, ch[N][alphabet], len[N], fail[N];
	char s[N];
	inline int newnode(int l){len[++sz] = l; fail[sz] = 0; memset(ch[sz], 0, sizeof sz); return sz;}
	inline void clear(){sz = -1; s[lst = cc = 0] = '$'; newnode(0); newnode(-1); fail[0] = 1;}
	inline int getfail(int x)
	{
		while (s[cc - len[x] - 1] != s[cc]) x = fail[x];
		return x;
	}
	inline void extend(char c)
	{
		s[++cc] = c;
		int now = getfail(lst);
		if (!ch[now][c - 'a']){int _ = newnode(len[now] + 2); fail[_] = ch[getfail(fail[now])][c - 'a']; ch[now][c - 'a'] = _;}
		lst = ch[now][c - 'a'];
	}
	inline void build(string s){for (char ch : s) extend(ch);}
	PAM(){clear();}
	~PAM() = default;
}T;

回文串

给一个字符串，求其所有回文子串在原串中出现的次数乘以这个子串的长度之最大值 .

PAM 跳的时候记录一下出现次数即可 .

Prüfer 序列

Prüfer 序列与树的转换

Prüfer 序列表明了一个完全图的生成树与数列之间的双射 .

即 Prüfer 序列可以将一个 $n$ 个结点的有标号的树用 $[1,n]$ 中的 $n-2$ 个整数表示 .

Prüfer 序列的建立方法：每次选择一个编号最小的叶结点并删掉它，然后在序列中记录下它连接到的那个结点。重复 $n$ 次后就只剩下两个结点 .

用堆实现是 $O(n\log n)$ 的 .

发现叶结点数是非严格单调递减的，要么删一个，要么删一个得一个，于是可以用一个指针维护一波，就是 $O(n)$ 了 .

从 Prüfer 序列生成树的方法是恰相反的 .

代码见 SoyTony 的博客 .

Cayley 公式及其推广

Cayley 公式

$n$ 个节点的有标号无根树有 $n^{n-2}$ 种 .

一些 exciting 的证法 .

根据 Prüfer 序列是双射的性质可以瞬间证明 .

推论 1

$n$ 个节点的有标号有根树有 $n^{n-1}$ 种 .

显然 .

推论 2

第 $i$ 个点度数为 $d(i)$ 的有标号无根树个数为

\[\dbinom{n-2}{d(1)-1,d(n)-1,\cdots,d(n)-1}=\dfrac{(n-2)!}{\displaystyle\prod_{i=1}^n(d(i)-1)!} \]

一个节点 $u$ 成为叶子节点之前每次删边都会在序列中出现，所以其在序列中出现次数为 $d(u)−1$ .

同时，编号最大的 $n$ 无论如何不会出现在序列当中，因此最后剩余的两个节点中，编号较大的一定是 $n$ .

于是多重组合数开整 .

推论 3

一个 $n$ 个点 $m$ 条边的带标号无向图有 $k$ 个连通块，我们希望添加 $k-1$ 条边使得整个图连通 .

令 $s_i$ 表示第 $i$ 个连通块的数量，则加边方案数为

\[n^{k-2}\cdot\prod_{i=1}^ks_i \]

看 OI Wiki，link .

例题：

UVA10843 Anne's game
洛谷 P4981 父子
HNOI2008 明明的烦恼
HNOI2004 树的计数

莫比乌斯反演

见 Möbius 反演注记 .

7.30（杂题）

斯坦纳树

杂题

7.31

启发式合并

普通启发式合并

可并堆

有 $n$ 个小根堆，每个堆包含且仅包含一个数，支持两种操作：

1 x y，将第 $x$ 个数和第 $y$ 个数所在的小根堆合并（若第 $x$ 或第 $y$ 个数已经被删除或第 $x$ 和第 $y$ 个数在用一个堆内，则无视此操作）.

2 x，输出第 $x$ 个数所在的堆最小数，并将这个最小数删除（若有多个最小数，优先删除先输入的；若第 $x$ 个数已经被删除，则输出 $-1$ 并无视删除操作）.

每次暴力合并，即把一个堆里元素一个个弹出来放到另一个堆里.

启发式：每次将较小的堆内的元素放到较大的堆里.

注意到对于每个点，如果它贡献一次操作的复杂度，那么它所在的堆的大小至少乘 2，故每个点最多贡献 $O(\log n)$ 次复杂度，于是总复杂度为 $O(n\log^2n)$ .

这就是启发式合并了 .

森林

维护一个森林，每个点有点权，支持：

Q x y k，查询点 $x$ 到点 $y$ 路径上所有的权值中，第 $k$ 小的权值是多少，保证点 $x$ 和点 $y$ 连通，同时这两个节点的路径上至少有 $k$ 个点 .

L x y，在点 $x$ 和点 $y$ 之间连接一条边，保证完成此操作后，仍然是一片森林 .

强制在线 .

注意到如果没有强制在线就是链上 kth，可以持久化线段树（主席树）实现 .

注意到有强制在线，所以我们考虑启发式合并，每次主席树合并小的合到大的上面，注意到我们需要维护加边求 LCA，可以倍增平凡实现 .

时间复杂度 $O(n\log^2n)$？

春节十二响

一棵树，每个点有点权，将所有点分为若干段，使得每段中各点均不存在父子关系 .

最小化每段点点权最小值之和 .

考虑一条链的情况，我们将 $1$ 点左右的左链 $L$ 和右链 $R$ 排序，只需要贪心的把内存占用排名相同的选上即可，正确性显然 .

于是推广到任意树，对于每个点用一个堆维护一下内存占用，合并即可每次取堆顶弹出，剩余的单算 .

分治，我们只需要把每个子树的答案合并，考虑启发式合并，可以证明时间复杂度为 $O(n\log n)$ .

Non-boring sequences

一个序列被称为是不无聊的，仅当它的每个连续子序列存在一个独一无二的数字，即每个子序列里至少存在一个数字只出现一次 . 给定一个整数序列，请你判断它是不是不无聊的 .

不要矩形面积并不要矩形面积并不要矩形面积并 .

对于每个区间都从两边同时向中间扫，判断每个数是否合法，若遇到合法的，则从该位置将该区间分裂为两个区间并递归处理 .

由于分裂一个区间的复杂度为较短区间的长度，所以其最劣复杂度 $O(n\log n)$ .

《启发式分裂》

Tip: Splay 启发式合并是 1log .

dsu on tree（静态链分治）

dsu on tree 的思路大概就是先轻重链剖分，然后每次信息维护的时候重儿子的直接继承上，然后再合并轻儿子信息 .

每个点到根最多有 $O(\log n)$ 条轻边，于是复杂度是正确的 .

Lomsat gelral

一个无根树，带点权，$q$ 次询问，每次询问某棵子树内，点权众数之和 .

作为一个板子我还是放代码吧：

CF600D Lomsat gelral

using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 114514;
int n;
ll a[N], siz[N], son[N], buc[N], ans[N], now, nowans;
vector<int> g[N];
inline void addedge(int u, int v){g[u].emplace_back(v);}
inline void ade(int u, int v){addedge(u, v); addedge(v, u);}
inline void dfs0(int u, int fa)
{
	siz[u] = 1;
	for (int v : g[u])
	{
		if (v == fa) continue;
		dfs0(v, u);
		siz[u] += siz[v];
		if (!son[u] || (siz[v] > siz[son[u]])) son[u] = v;
	}
}
inline void ins(int x)
{
	++buc[x];
	if (buc[x] == now) nowans += x;
	if (buc[x] > now){now = buc[x]; nowans = x;}
}
inline void cls(int u, int fa)
{
	--buc[a[u]];
	for (int v : g[u])
		if (v != fa) cls(v, u);
}
inline void insd(int u, int fa)
{
	ins(a[u]);
	for (int v : g[u])
		if (v != fa) insd(v, u);
}
inline void dfs(int u, int fa, bool clr)
{
	for (int v : g[u])
		if ((v != fa) && (v != son[u])) dfs(v, u, true);
	if (son[u]) dfs(son[u], u, false);
	for (int v : g[u])
		if ((v != fa) && (v != son[u])) insd(v, u);
	ins(a[u]); ans[u] = nowans;
	if (clr){now = nowans = 0; cls(u, fa);}
}
int main()
{
	scanf("%d", &n);
	for (int i=1; i<=n; i++) scanf("%lld", a+i);
	for (int i=1, u, v; i<n; i++) scanf("%d%d", &u, &v), ade(u, v);
	dfs0(1, 0); dfs(1, 1, 0);
	for (int i=1; i<=n; i++) printf("%lld ", ans[i]);
	return 0;
}

Weak Dokhtar-kosh

$n$ 个点的树，每个点有点权，问至少改变几个点权才能使得任意一条路径的权值异或和不为 $0$ .

考虑贪心，我们只需维护这个点是否需要改变，剩下的 dsu on tree .

差分约束

差分约束基础内容 .

Cashier Employment

一天中 $0$ 到 $23$ 总共24个时刻，时刻 $i$ 至少需要 $R(i)$ 个人，现在有 $m$ 个人应聘，每个人开始的工作时间为 $t_i$，且每个人都要工作八小时，求需要的最少人数 .

无脑打不等式（需建超级源点转为差分约束问题），然后不等式不够所以要枚举一下 $R(24)$ .

整个图就 $24$ 个点咋写都能过 .

2-SAT

网络流

posted @ 2022-07-20 11:26 yspm 阅读(295) 评论(11) 编辑收藏举报

刷新页面返回顶部

Jijidawang

2022 暑假 🐍🐋

7.20

二维凸包

Andrew 算法

动态凸包

树的直径与重心

树的直径

树的重心

cdq 分治

简要思想

三维偏序

优化 DP

对时间维分治

虚树

7.22

BSGS

整体二分

决策单调性

7.25

线性基

定义与构建

经典问题

基环树

Catalan 数

wqs 二分

7.26

可持久化数据结构

数位 DP

\(k\)-D Tree

点分治

7.27

圆方树

AC 自动机

01 分数规划

李超线段树

7.29

Manacher

回文自动机 / 回文树

定义与构建

Prüfer 序列

Prüfer 序列与树的转换

Cayley 公式及其推广

莫比乌斯反演

7.30（杂题）

斯坦纳树

杂题

7.31

启发式合并

普通启发式合并

dsu on tree（静态链分治）

差分约束

2-SAT

网络流

公告