Jijidawang

由竞赛图的分数序列构造出竞赛图

2022/6/14 我终于来到了机房，开始更这篇文章 QwQ

目录

兰道定理 (Landau's Theorem)

内容

一个竞赛图（tournament）定义为给一个无向完全图每条边定向后得到的图 .

定义一个竞赛图的比分序列（score sequence），是把竞赛图的每一个点的出度从小到大排列得到的序列 .

Landau's Theorem

一个不降序列 \(\{s_n\}\)（\(n\ge 1\)）是合法的比分序列当且仅当

\[\forall 1\le k\le n, \sum_{i=1}^ks_i\ge\dbinom k2 \]

且当 \(k=n\) 时必须取等号 .

证明

UPD. Mark 一个神奇证明 .

复读：https://blog.csdn.net/a_crazy_czy/article/details/73611366 .

必要性显然，下面证充分性 .

假设有一个满足条件的序列 \(\{s\}\)，我们考虑构造一个竞赛图 \(S\) 使得其比分序列为 \(\{s\}\) .

考虑从一个平凡的竞赛图 \(T_n\) 逐步调整到目标竞赛图 .

\(T_n\) 从第 \(i\) 个节点向所有满足 \(j<i\) 的 \(j\) 节点都连有向边，于是其比分序列就是 \(\langle0,1,2\cdots,n-1\rangle\) .

考虑当前构造到了一个竞赛图 \(U\)，它的比分序列 \(\{u\}\) 满足

\[\forall 1\le k\le n, \sum_{i=1}^ks_i\ge\sum_{i=1}^ku_i \]

\(k=n\) 时取等号 . 显然初始的 \(U=T_n\) 是满足这个条件的 .

我们令 \(\alpha\) 是第一个满足 \(s_{\alpha}>u_{\alpha}\) 的位置， \(\beta\) 是最后一个满足 \(u_{\alpha}>u_{\beta}\) 的位置， \(\gamma\) 是第一个满足 \(s_{\gamma}<u_{\gamma}\) 的位置 .

存在性：\(\alpha\)，\(\beta\) 显然存在 . 因为 \(k=n\) 时取等号，根据 \(\beta\) 的定义有 \(\beta\) 到 \(n\) 直接一定存在满足条件的 \(\gamma\) .

考虑随便一个 \(\zeta\in(\beta,\gamma)\)，必然有 \(u_{\beta}<u_{\zeta}<u_{\gamma}\)，又所有元素都是整数，故 \(u_{\gamma}\ge u_{\beta}+2\) .

可以通过大概这样一个图来理解：

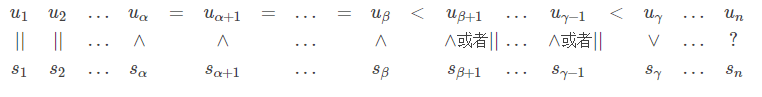
（蒯 复读的 csdn 的）

因为 \(u_{\gamma}\ge u_{\beta}+2\)，那么一定存在一个点 \(\lambda\in(\beta,\gamma)\) 使得存在有向边 \(\gamma\to\lambda\) 和 \(\lambda\to\beta\) .

然后我们翻转这两条边，就构造出一个新竞赛图 \(U'\)，而且仍然满足

\[\forall 1\le k\le n, \sum_{i=1}^ks_i\ge\sum_{i=1}^ku_i \]

且 \(k=n\) 时取等号 .

这样一直构造就可以得到所要求的竞赛图，证明如下：

对于比分序列分别是 \(\{u_n\},\{s_n\}\) 竞赛图 \(U,S\)，定义它们的曼哈顿距离为

\[\operatorname{dist}(U,S)=\sum_{i=1}^n|u_i-s_i| \]

显然经过边翻转后一定有 \(\operatorname{dist}(U',S)=\operatorname{dist}(U,S)+2\) .

又因为题设，任意时刻都有 \(\displaystyle \sum_{i=1}^ns_i=\sum_{i=1}^nu_i\)，故 \(\operatorname{dist}(U,S)=0\pmod 2\)（mod 2 意义下可以直接去掉绝对值）.

从而我们就可以由上面的流程用 \(\dfrac 12\operatorname{dist}(T_n,S)\) 步构造出满足条件的图 \(S\) .

构造

证明中已经写出了构造的流程！

由竞赛图的分数序列构造竞赛图 
#include <bits/stdc++.h>
#define file(x) {freopen(x".in", "r", stdin); freopen(x".out", "w", stdout);}
#define twicecat(p, q) p##p##q
#define twiceline(t) twicecat(_, t)
template<typename T>
inline T chkmin(T& x, const T& y){if (x > y) x = y; return x;}
template<typename T>
inline T chkmax(T& x, const T& y){if (x < y) x = y; return x;}
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int N = 5555;
int n, s[N], u[N], cc[N], a[N][N];
bool check()
{
	int now = 0;
	for (int i=1; i<=n; i++)
	{
		now += s[i];
		if (now < i * (i-1) / 2) return false;
		if ((i == n) && (now > i * (i-1) / 2)) return false;
	} return true;
}
inline void sortu()
{
	memset(cc, 0, sizeof cc);
	for (int i=1; i<=n; i++) ++cc[u[i]];
	int ptr = 0;
	for (int i=1; i<=n; i++)
	{
		while (!cc[ptr]) ++ptr;
		--cc[ptr]; u[i] = ptr;
	}
 } 
int main()
{
	scanf("%d", &n);
	for (int i=1; i<=n; i++) scanf("%d", s+i);
	stable_sort(s+1, s+1+n);
	if (!check()){puts("-1"); return 0;}
	for (int i=1; i<=n; i++)
		for (int j=1; j<i; j++){a[i][j] = 1; ++u[i];}
	while (true)
	{
		bool ok = true;
		for (int i=1; (i<=n) && ok; i++) ok = (s[i] == u[i]);
		if (ok) break;
		int alpha = -1, beta = -1, gamma = -1;
		for (int i=1; i<=n; i++)
			if (s[i] > u[i]){alpha = i; break;}
		for (int i=n; i>=1; i--)
			if (u[alpha] == u[i]){beta = i; break;}
		for (int i=1; i<=n; i++)
			if (s[i] < u[i]){gamma = i; break;}
		for (int i=1; i<=n; i++) // i ==> lambda
			if (a[gamma][i] && a[i][beta]){a[gamma][i] = a[i][beta] = false; a[i][gamma] = a[beta][i] = true; --u[gamma]; ++u[beta]; break;}
		sortu();
	}
	for (int i=1; i<=n; i++)
		for (int j=1; j<=n; j++)
			if (a[i][j]) printf("%d %d\n", i, j);
	return 0;
}

时间复杂度大概是 \(O(n^2+n\operatorname{dist}(T_n,S))\)，然而我不会算 \(\operatorname{dist}\) 的量级，就放一个可能松的上界 \(O(n^3)\) 吧 .

一道例题

CF850D Tournament Construction

给一个去重了的比分序列 \(\{a_m\}\)，构造一个满足条件的点数最小的竞赛图 .

\(m\le 31\)，\(a_i\le 30\) .

题解

关键就是通过去重的序列还原出真正的比分序列，这样就可以按上面的流程构造了 .

假设真正的点数为 \(n\)，则原图最多有 \(n\max_i\{a_i\}\) 条边，而竞赛图恰有 \(\dfrac{n(n-1)}2\) 条边，解得 \(n\le 61\) .

首先给 \(\{a\}\) 排序 .

根据 Landau's Theorem 可以知道真正的比分序列 \(\{s\}\) 满足

\[\forall 1\le k\le n, \sum_{i=1}^ks_i\ge\dbinom k2 \]

于是我们可以考虑构造一个合法的 \(\{s\}\)，在 \(\{a\}\) 中选数且每个数至少用一次 .

枚举点数背包即可，因为要还原序列所以要记录一下方案 .

代码也是非常好写：

CF850D 
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int N = 62, M = 1831;
int n, _a[N], s[N], u[N], cc[N], a[N][N], sav[N][N][M];
bool dp[N][N][M];
inline void sortu()
{
	memset(cc, 0, sizeof cc);
	for (int i=1; i<=n; i++) ++cc[u[i]];
	int ptr = 0;
	for (int i=1; i<=n; i++)
	{
		while (!cc[ptr]) ++ptr;
		--cc[ptr]; u[i] = ptr;
	}
}
inline bool redu()
{
	stable_sort(_a+1, _a+n+1); dp[0][0][0] = 1;
	for (int i=1, y; i<=n; i++)
		for (int j=i; j<N; j++)
			for (int k=i-1; k<j; k++)
				for (int x=k*(k-1)/2; x<M; x++)
				{
					y = x + (j-k) * _a[i];
					if (y >= M) break;
					if (dp[i-1][k][x]){dp[i][j][y] = true; sav[i][j][y] = j-k;}
				}
	int real_n, lst_n = n;
	for (real_n = n; real_n < N; real_n++)
		if (dp[n][real_n][real_n*(real_n-1)/2]) break;
	if (real_n == N) return false;
	printf("%d\n", n = real_n);
	int j = n, k = n * (n-1) / 2;
	for (int i=lst_n, t; i; i--)
	{
		for (int p=0; p<=sav[i][j][k]; p++) s[j-p] = _a[i];
		t = j;
		j -= sav[i][t][k]; k -= sav[i][t][k] * _a[i];
	} return true;
 } 
int main()
{
	scanf("%d", &n);
	for (int i=1; i<=n; i++) scanf("%d", _a+i);
	if (!redu()){puts("=("); return 0;}
	stable_sort(s+1, s+1+n);
	for (int i=1; i<=n; i++)
		for (int j=1; j<i; j++){a[i][j] = 1; ++u[i];}
	while (true)
	{
		bool ok = true;
		for (int i=1; (i<=n) && ok; i++) ok = (s[i] == u[i]);
		if (ok) break;
		int alpha = -1, beta = -1, gamma = -1;
		for (int i=1; i<=n; i++)
			if (s[i] > u[i]){alpha = i; break;}
		for (int i=n; i>=1; i--)
			if (u[alpha] == u[i]){beta = i; break;}
		for (int i=1; i<=n; i++)
			if (s[i] < u[i]){gamma = i; break;}
		for (int i=1; i<=n; i++) // i ==> lambda
			if (a[gamma][i] && a[i][beta]){a[gamma][i] = a[i][beta] = false; a[i][gamma] = a[beta][i] = true; --u[gamma]; ++u[beta]; break;}
		sortu();
	}
	for (int i=1; i<=n; i++, puts(""))
		for (int j=1; j<=n; j++) putchar(a[i][j] + '0');
	return 0;
}

Bonus

定义 \(dp_{i,j,k}\) 表示构建出原图的点数为 \(j\)，共有 \(k\) 条边且去重后为 \(a_{1\dots i}\) 的图是否存在 .

于是可以转移：

\[dp_{i,j,k}=dp_{i-1,j-1,k-a_i}\lor dp_{i,j-1,k-a_i} \]

这样 DP 部分就是 \(O(mM)\) 的了，其中 \(M\) 是边数 .

posted @ 2022-06-11 17:14  Jijidawang  阅读(184)  评论(4)  编辑  收藏  举报
😅​