Border Theory
主要是抄论文。。
I. 基础定义
基本定义
假设都知道串串是啥 .
其实正片文章都在混淆字符串 和字符串 的长度 ,意会一下 .
约定:
- 的长度是 .
- 是字符集 .
- 是子串 .
- 是 的第 个字符, 也是 .
- 字符串 拼接:.
- 长度为 的前缀、后缀:, .
- 然后如果一个 满足对一个串串 都有 ,则 是 的一个周期(period),若 则称为整周期 .
- 的最小周期的长度记为 .
若俩字符串 满足:
- .
- 即是 的前缀又是后缀 .
则称 是 的一个 border .
定义 表示 的所有 border 构成的集合 .
长度最长的 border 记作 .
后面叙述大概隐含一个 原串 ,所有 border 都是 的 border .
Period 与 Border
是 的 border 是 的周期,如图(或者看 这个) .

前缀函数 / KMP 自动机
因为 的所有 border 都是 的前缀,所以我们可以用一个下标表示出来 .
定义 表示 的最长 border 长度 .
有可能你会发现 就是只有一个串串 的 AC 自动机的 fail 指针 .
然后显然有
定理
这个非常显然吧 .
然后显然 border 的 border 还是 border,所以我们不断跳这个 就能求出全部 border 了 .
习题:Seek the Name, Seek the Fame .
KMP 算法
这块可以跳过去 .
KMP 大概就是 AC 自动机跳的过程
习题:
Border 树 / 失配树
对于每个 ,连边 ,就成了 border 树(或者叫失配树).
然后剩下的就看题吧 .
一个串串 ,多组询问,求两个前缀的最长公共 border .
border 树上每个点的祖先都是它的 border .
然后点的定义就是前缀 .
于是题目要求的这玩意就是 border 树上 LCA,没了 .
求给定字符串所有前缀的最大周期长度之和 .
周期和 border 对应,于是问题转换为求每个前缀的最小非空 border .
是不是就是 border 树上最浅祖先啊,暴跳就完了 .
求 的每个前缀 长度一半的 border 个数 .
当时学 KMP 的时候就是混过去的,现在终于知道咋做了,,,
建出 border 树,然后因为答案具有单调性,可以分两种做法:
- 倍增 .
- 大概是做一个限制长度的 KMP,然后复杂度可以均摊??
II. 性质与定理
关于周期的基本定理
定理 (Weak Periodicity Lemma,WPL)
一个字符串 ,若其有长度为 和 的周期,且 ,则 有长度为 的周期 .
不失一般性,设 ,考虑证明 也是周期,就可以辗转相减搞出 了 .
根据 period 的定义,:
- 当 时, .
- 当 时, .
即 。,从而 是周期 .
Q.E.D.
Bonus:
Periodicity Lemma
一个字符串 ,若其有长度为 和 的周期,且 ,则 有长度为 的周期 .
定理
对于串串 ,若 ,则 在 中的匹配位置必为等差序列 .
显然只需要考虑匹配至少 次的情况 .
考虑 在 中的第 次匹配 ,还有随便一个匹配 .
设 间距为 , 间距为 ,如图 .
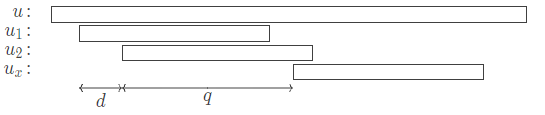
(因为 cnblogs 的 不支持 \xleftrightarrow 于是换成图片了)
不难发现 都是 的周期,于是根据 WPL, 亦然 .
设 的最小周期为 ,显然 ,可以考虑反证法 WPL .
然而 显然是 的周期,于是 也是 的周期吧 .
若 ,将 右移 又形成一次匹配,矛盾!
于是显然可以推出 .
又 ,从而 .
看看 意味着啥?是不是就证完了 .
Q.E.D.
推论(?):
对于串串 ,若 ,则 在 中的匹配位置形成等差序列 .
若它的项数不小于 ,则其公差等于 的最小周期 .
Border 的结构
定理
的长度不小于 的 border 长度构成一个等差序列 .
设长度最大的 border 为 ,另一个 border 长度为 (即 是周期,且均有 .
由 WPL 得 也是 的周期,所以存在长度为 的 border .
根据 为最长 border 的假设,要满足 即 .
这个整除意味着等差序列,和上面那个 定理 类似 .
长度小的 border?
定理
的所有 border 长度构成 个等差序列 .
首先,将该串的长度达到 的 border 划分成一个等差序列 .
然后取出长度最小的 border .
然后可以证明 ,如下 .
- 若最小循环节 ,不断从最长 border 减去 则必然有 .
- 若最小循环节 ,则直接证完 .
然后根据我们平凡的 定理 ,其他 border 都是这个 的 border,于是每次缩小 ,就是 级别的了 .
Q.E.D.
Bonus:更紧的界: .
Prefix-Suffix (PS)
将 的所有 border 按长度分类:
若 ,记 .
是不是很像 border!!
然后令 .
则 在 内的 border 长度集合就是 .
定理
构成一个等差数列 .
都是 的 border,可以看金策大爷的图 .
然后我们发现 定理 其实是这玩意的推论 .
III. 一些问题
子串周期查询
一个长度为 的字符串 ,每次询问一个子串 的所有周期 .
用 个等差序列表示 .
所有周期等价于询问所有 border .
按 border 长度 分类:
- Case 1. .
- Case 2. .
根据前面说的啥 ,我们可以知道 Case 1 就是要求 .
若 是一个 Large Prefix-Suffix (LargePS),则 是 的前缀, 是 的后缀 .
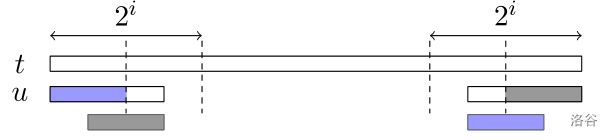
求出 在 中匹配的所有位置,还有 在 中匹配的所有位置,移位取交集即可 .
Case 2: 因为 ,所以我们的任务 — 求出 的所有长度不小于 的 border,是不是就是求 啊,和 Case 1 做法相同 .
然后我们看看具体怎么做:
Task 1. 怎么求出匹配的所有位置???
Internal Pattern Matching (Easy ver.)
一个字符串 ,多次询问,每次给出其两个子串 (满足 ),询问 在 中的所有匹配位置 .
特殊性质: 是 的幂 .
也就是要实现一个 ,能求出 在 原串 中起点不小于 的第一次匹配(以及反过来的 ).
因此只需要把 中所有长度为 的次幂的子串拉出来排序,相同的子串按起始位置排序即可 .
这个过程类似于倍增求 SA .
然后查 的时候二分就完了 .
Task 2. 等差序列取交集???
可以证明俩等差序列公差相等,具体比较牛逼,看金策大爷的课件吧 .
于是我们目前做到的是:
- 空间 .
- 预处理 ,询问 .
- 在线 .
的算法 .
一个小优化:
注意到 询问时只关系起点在 的匹配 .
于是将 按 的间隔分段,每段是一个等差数列 .
所有非空段的东西丢进 Hash Table,就可以单次一个 了 .
预处理期望 .
子串周期查询可以在 BJWC Border 的四种求法 测(题目要求区间最大 Border 长度).
Internal Pattern Matching (IPM)
一个字符串 ,多次询问,每次给出其两个子串 (满足 ),询问 在 中的所有匹配位置 .
我们是不是解决了 是二的幂的情形,而且还做到了 询问?
如果不是你就等差数列移位求交集,复杂度变成询问 .
等差数列移位求交集的过程是不是类似 ST 表啊
子串循环同构判定
一个字符串 ,多次询问,每次给出其两个长度相等的子串 ,询问 是否循环同构 .
如果是就输出所有移位长度(表示成等差序列) .
我会最小表示法!
几个平凡的结论:
- 一个串串 的最小周期是 ,如果 ,则 只有 个本质不同的循环移位,每种出现 次 .
- 循环同构 是 的子串 .
根据第二个是不是 IPM 判定就好了?
然后我们看看怎么求所有移位长度 .
设 ,,不失一般性,令 .
记 ,IPM 查询 在 中出现的所有位置 (是一个公差为 的等差序列)
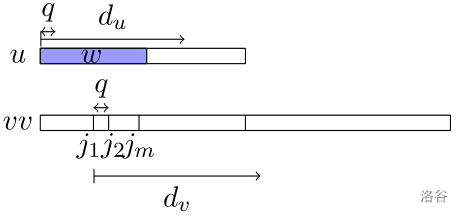
根据 定理 的推论,当 时, .
设
- 最长的拥有周期 的前缀长度为 .
- 最长的拥有周期 的前缀长度为 .
于是 是合法起始点的必要条件就是 .
然后就可以轻易 求移位长度了 .
Reference
以下是博客签名,正文无关
本文来自博客园,作者:yspm,转载请注明原文链接:https://www.cnblogs.com/CDOI-24374/p/16009595.html
版权声明:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议(CC BY-NC-SA 4.0)进行许可。看完如果觉得有用请点个赞吧 QwQ



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】