丽泽普及2022交流赛day17 社论

http://zhengruioi.com/contest/1088

SoyTony 重新 rk1 .

stO SoyTony Orz

省流：俩计数 .

目录

目录

• A
  • 题面
  • 题解
    • Key
    • 算法 1（SoyTony）
    • 算法 2（he_____he）
    • 算法 3
• B
  • 题面
  • 题解
    • 乱搞（artalter）
    • 算法
• C
  • 题面
  • 题解
    • 算法
• D
  • 题面
  • 题解
    • dp
    • Bonus

时间复杂度瞎算的 .

A

题面

一个 $n\times m$ 的字符矩阵，从左上走到右下，只能往右往下走，问经过路径字典序最小是啥 .

题解

Key

每个字符贪心地走，当且仅当往右和往下字符相同时可能有两种后继状态

算法 1（SoyTony）

BFS .

算法 2（he_____he）

提交记录 .

口胡一下，可能理解错了 .

考虑 dp，由于字符串显然存不下（会 MLE），于是考虑维护排名 .

动态维护排名即可，因为合法的排名不会很多 .

算法 3

等价于 算法 1

按照走的步数枚举算贡献并标记转移点即可 .

B

题面

有 $n$ 个玻璃杯，每杯里都有水 .

把这 $n$ 杯里的水互相倒，最终使得只有 $k$ 个杯子里有水。

易知从把水从第 $i$ 个玻璃杯倒到第 $j$ 个花费是 $c_{i,j}$，求最小花费。

题解

乱搞（artalter）

首先这个玩意可以按最小生成树走 .

但是这个贪心显然是错的，于是我们钦定两条边然后暴力算最小生成树答案取最优 .

然后……就过了？（

算法

状压 dp，令 $dp_S$ 表示 $S$ 集合有水的最小花费，枚举一次倒水即可 .

时间复杂度 $O(2^nn^2)$ .

C

题面

一张 $n$ 个点的无向完全图，问边权范围 $1\sim L$，且 $1\to n$ 最短路为 $k$ 的图数量 .

（BZOJ3868）

题解

算法

显然最短路大于 $k$ 就没用了，可以直接设为 $k+1$ .

枚举最短路为 $s$ 的点数量 $t_s$，于是可以钦定一个顺序算一下每个点到 $1$ 的最短路 $d$ .

考虑算边权的取值：

• 若 $d_u=d_v$，显然 $w(u,v)$ 取啥都行 .
• 若 $d_u<d_v$，则边权不能小于 $d_v-d_u$，要不然会破坏最短路 .
• 若 $d_u>d_v$，和上面类似 .

那么边权就有 $L-(d_u-d_v)+1$ 种可能（$d_u>d_v$）

但是发现 $d_u$ 的最短路性质必须要有一个至少一个 $v$ 来保证 $d_v + w(v,u) = d_u$（能取到最短路）.

然而使得那个柿子成立的边权 $w$ 有 $L-(d_u-d_v)$ 种可能（如果 $d_u\ge k$ 这玩意就没贡献了，要丢掉）.

于是目前的总方案数就是

$$ans = \prod(L-(d_u-d_v)+1) - \prod(L-(d_u-d_v))$$

然而我们枚举的是最短路为 $s$ 的点数量 $t_s$，没有顺序（注意相同数）所以要再乘一个 $(n-2)!/$，然后因为重复要除以一个 $\prod a_i$ .

时间复杂度 $O\left(\dbinom nkn^2\log n\right)$（抄的别的博客的，存疑）

---

这题真的牛逼，，，

似乎可以说是大力枚举题钓鱼/kx

D

题面

一个 $n$ 个点的无向图，若满足：

1. 无重边自环
2. 删掉一条边或加上一条边后，满足 $1$ 且存在一条欧拉回路

则称其是可爱的 .

求 $n$ 个点可爱图个数，对 $10^9+7$ 取模 .

两个图不同当且仅当某条边 $(u,v)$ 恰好只存在于某一个图中

题解

dp

显然题目等价于 $n$ 点欧拉图个数乘上 $\dbinom n2$ .

令 $f_n$ 表示 $i$ 个点的欧拉图数量，$g_n$ 表示 $n$ 个点度为偶数的无向图数量 .

众所周知图存在欧拉回路当且仅当没有奇点 .

于是考虑加一个点，容斥掉不连通的

如果原图存在一个欧拉子图，那么 $i$ 必然要连另外一方面，因为要保持性质，$i$ 必须连奇点，于是就不连通了（$i$ 连所有奇点） .

$g_n$ 显然等于 $2^{\tbinom{n-1}2}$（钦定 $n-1$ 个点随便连，剩下那个点用来平衡奇度点），于是递推式就是

$$f_n=g_n-\sum_{i=1}^{n-1}f_ig_{n-i}\dbinom{n-1}{i-1}$$

Bonus

zero4338 说 $f$ 的 EGF 是 $g_{n-1}$ 的 EGF 的 $\ln$ .

然后由于神秘的模 $10^9+7$，分治 ntt 俩 $\log$，MTT 一 $\log$ .

我打不出代码来验证不了正确性，不过 zero 爷说的话哪里会有错呢？/kx

details .

（众所周知这个 $g$ 可以 $O(1)$ 求）

---

我草有原题，叫 建设游乐园，百度能搜到 题解 .

$\ln$ 的结论是对的，等我变强后看看为啥吧 qwq .

---

zero4338 只说了连通图个数 EGF 是随便图个数 EGF 的 $\ln$ .

但是这玩意和欧拉图个数有啥关系啊 /yun .
upd. 度数都为偶数的图可以分成若干个欧拉图 —— zero4338

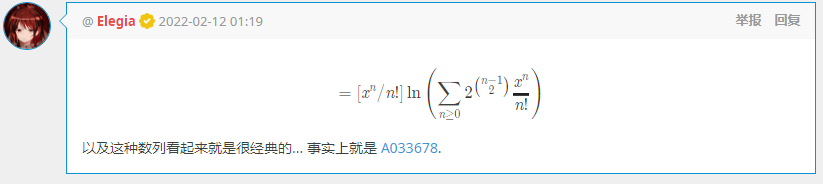
然而 EI 给出了一模一样的式子，并丢了一个 OEIS 序列（我搜不到是因为我第一项错了qwq）：

颤抖，颤抖。