欧拉公式的一个简洁证明

平面图大坑啊，我不打算填了 qwq

---

目录

• 基本内容
  • 基本定义
  • 欧拉公式
• 光速证明欧拉公式
  • 正片
  • 扩展阅读
• Reference

基本内容

如果知道了就可以直接跳过了 .

基本定义

平面图 定义

若图 $G$ 能被画在平面上且不同的边仅在端点处相交，则称图 $G$ 为平面图 . 画出的没有边相交的图称为 $G$ 的平面表示或平面嵌入 .

---

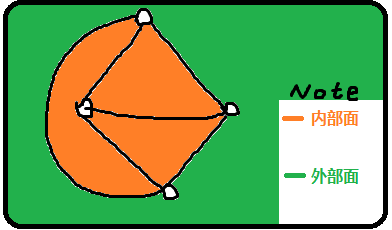
面 定义

一个图的平面嵌入会将整个平面划分成若干个互不连通的区域，每个区域称为一个面 . 无界的区域称作外部面，有界的区域称作内部面 . 包围某个面的所有边构成了该面的边

---

对偶图 定义

设 $G$ 为平面图的一个平面嵌入，定义它的对偶图 $G^∗$ 为：

1. 在 $G$ 中的每一个面取一个点，作为 $G^∗$ 的顶点；
2. 对于 $G$ 中的每一条边 $e$，都对应一条 $G^∗$ 中的边 $e^∗$ 连接与 $e$ 相邻的两个面中的顶点，且 $e^*$ 在平面中穿过 $e$ .

欧拉公式

首先要明确我们到底要证什么吧，欧拉公式有好多啊 qwq .

平面图欧拉公式

对于一个连通的平面嵌入 $G$，它的点数 $V$，边数 $E$，面数 $F$ 满足关系式

$$V-E+F = 2$$

推论：

对于一个有 $k$ 个连通块的平面嵌入 $G$，它的点数 $V$，边数 $E$，面数 $F$ 满足关系式

$$V-E+F = C+1$$

推论的证明：

对 $G$ 的每个连通块 $G_{1\cdots k}$ 用 Euler's Formula，得

$$V_i-E_i+F_i=2\quad 1\le i\le k$$

相加，得

$$\sum V_i - \sum E_i + \sum F_i = 2k$$

而显然 $\displaystyle \sum V_i = V,\, \displaystyle \sum E_i = E,\, \displaystyle \sum F_i = F+(k-1)$（$F$ 的式子因为外部面多计算了 $k-1$ 次） .

从而 $V-E+F+(k-1) = 2k$，即 $V-E+F = k+1$ . 证毕 .

光速证明欧拉公式

正片

考察图 $G$ 的一棵生成树 $\mathcal T$ 以及其对偶图 $G^{*}$ .

显然 $G$ 的非生成树边对应 $G^{*}$ 中也形成一棵生成树 $\mathcal T^{*}$ .

众所周知，树的边数等于点数减一 .

设生成树边数为 $e$，于是

• $V$，即 $G$ 的顶点数，则 $V=e+1$ .
• $F$，即 $G^{*}$ 的顶点数，则 $F=e+1$ .
• $E$，即 $\mathcal T,\mathcal T^{*}$ 的边数和，则 $E=2e$ .

从而

$$\begin{aligned}V-E+F&=e+1-2e+e+1\\&=2\end{aligned}$$

证毕

扩展阅读

• Cauchy 的证明
• 归纳法
• 平面图。。

Reference

• 平面图欧拉公式的精彩证明 - _beginend
• 浅谈平面图相关算法 - 唐绍轩（WC 2022）
• 欧拉公式 -百度百科
• 《图论及其应用》学习笔记（平面图） - HeinSven