走迷宫 简要题解

走迷宫 简要题解

题面

走迷宫，带起点终点 .

有传送门，传送门个数不超过 \(26\) 个 .

做法

BFS

不会 .

显式建图

我们可以考虑把每个点能到的点连边 .

二维压到一维，常见 Trick .

于是我们有一个很显然的想法：点到传送门连 \(0\) 权值的边 .

但是这样是错的，因为我们经过传送门必须得进去 .

e.g.

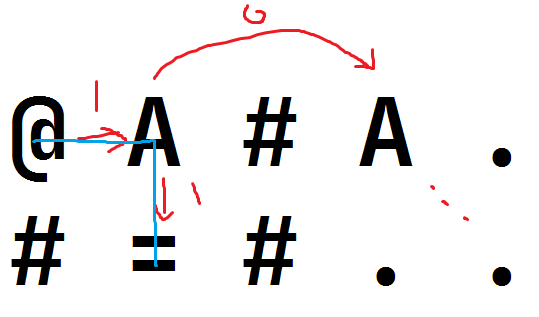
红色是边，蓝色是最短路 .

于是如果一个点能到传送门，我们就直接把传送门能到的点和它连边，这样就好了 .

注意要严格连单向边 .

这样每条边的权值就都是 \(1\) 了，BFS 也能求最短路了 .

显式建图的 BFS 显然跑不过直接 BFS 啊/kk

代码

Dijkstra

#include <iostream>
#include <cmath>
#include <ctime>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <cstring>
#include <queue>
#include <map>
#include <set>
#define file(s) freopen(s".in", "r", stdin); freopen(s".out", "w", stdout);
using namespace std;
typedef pair<int, int> pii;
const int rN = 333, N = rN*rN, dx[] = {1, -1, 0, 0}, dy[] = {0, 0, 1, -1};
vector<pii> g[N];
string s;
int n, m, dis[N];
bool vis[N], v[rN][rN];
map<char, pii> tmp;
map<pii, pii> portal;
pii st, ed;
inline void addedge(int u, int v, int w){g[u].push_back(make_pair(v, w));}
inline void ade(int u, int v, int w){addedge(u, v, w); addedge(v, u, w);}
struct Node
{
	int idx, d;
	Node(int _=0, int __=0){idx = _; d = __;}
	inline bool operator <(const Node& a)const{return d>a.d;}
};
void dijkstra(int s)
{
	memset(dis, 0x3f, sizeof dis);
	memset(vis, false, sizeof vis);
	priority_queue<Node> q; dis[s]=0; q.push(Node(s, dis[s]));
	while (!q.empty())
	{
		auto now = q.top(); q.pop();
		int u = now.idx;
		if (vis[u]) continue;
		vis[u] = true;
		for (auto _ : g[u])
		{
			int v = _.first, w = _.second;
			if (vis[v]) continue;
			if (dis[v] > dis[u]+w){dis[v] = dis[u]+w; q.push(Node(v, dis[v]));}
		}
	}
}
int trans(pii _){return _.first * 303 + _.second;}
int main()
{
	file("maze");
	scanf("%d%d", &n, &m);
	for (int i=1; i<=n; i++)
	{
		cin>>s;
		for (int j=0; j<m; j++)
		{
			pii now = make_pair(i, j+1);
			if (s[j] == '#') v[i][j+1] = true;
			else if (s[j] == '@') st = now;
			else if (s[j] == '=') ed = now;
			else if (s[j] == '.') ;
			else
			{
				auto it = tmp.find(s[j]);
				if (it != tmp.end()) portal[it->second] = now, portal[now] = it->second; 
				else tmp[s[j]] = now;
			}
		}
	}
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++)
		{
			if (v[i][j]) continue;
			auto now = trans(make_pair(i, j));
			for (int k=0; k<4; k++)
			{
				int x = i + dx[k], y = j + dy[k];
				if ((x<1) || (y<1) || (x>n) || (y>m)) continue;
				if (v[x][y]) continue;
				auto it = portal.find(make_pair(x, y));
				if (it != portal.end()) addedge(now, trans(it->second), 1);
				else addedge(now, trans(make_pair(x, y)), 1);
			}
		}
	dijkstra(trans(st));
	if (dis[trans(ed)] == dis[0]) puts("-1");
	else printf("%d\n", dis[trans(ed)]);
	return 0;
}

BFS

#include <iostream>
#include <cmath>
#include <ctime>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <cstring>
#include <queue>
#include <map>
#include <set>
#define file(s) freopen(s".in", "r", stdin); freopen(s".out", "w", stdout);
using namespace std;
typedef pair<int, int> pii;
const int rN = 333, N = rN*rN, dx[] = {1, -1, 0, 0}, dy[] = {0, 0, 1, -1};
vector<int> g[N];
string s;
int n, m, dis[N];
bool vis[N], v[rN][rN];
map<char, pii> tmp;
map<pii, pii> portal;
pii st, ed;
inline void addedge(int u, int v){g[u].push_back(v);}
inline void ade(int u, int v){addedge(u, v); addedge(v, u);}
struct Node
{
	int idx, d;
	Node(int _=0, int __=0){idx = _; d = __;}
	inline bool operator <(const Node& a)const{return d>a.d;}
};
void bfs(int s)
{
	memset(dis, 0x3f, sizeof dis);
	memset(vis, 0, sizeof vis);
	queue<int> q; q.push(s); dis[s] = 0;
	while (!q.empty())
	{
		int u = q.front(); q.pop();
		if (vis[u]) continue;
		vis[u] = true;
		for (auto v : g[u])
		{
			if (vis[v]) continue;
			q.push(v); dis[v] = min(dis[v], dis[u] + 1);
		}
	}
}
int trans(pii _){return _.first * 303 + _.second;}
int main()
{
	file("maze");
	scanf("%d%d", &n, &m);
	for (int i=1; i<=n; i++)
	{
		cin>>s;
		for (int j=0; j<m; j++)
		{
			pii now = make_pair(i, j+1);
			if (s[j] == '#') v[i][j+1] = true;
			else if (s[j] == '@') st = now;
			else if (s[j] == '=') ed = now;
			else if (s[j] == '.') ;
			else
			{
				auto it = tmp.find(s[j]);
				if (it != tmp.end()) portal[it->second] = now, portal[now] = it->second; 
				else tmp[s[j]] = now;
			}
		}
	}
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++)
		{
			if (v[i][j]) continue;
			auto now = trans(make_pair(i, j));
			for (int k=0; k<4; k++)
			{
				int x = i + dx[k], y = j + dy[k];
				if ((x<1) || (y<1) || (x>n) || (y>m)) continue;
				if (v[x][y]) continue;
				auto it = portal.find(make_pair(x, y));
				if (it != portal.end()) addedge(now, trans(it->second));
				else addedge(now, trans(make_pair(x, y)));
			}
		}
	bfs(trans(st));
	if (dis[trans(ed)] == dis[0]) puts("-1");
	else printf("%d\n", dis[trans(ed)]);
	return 0;
}