浅谈并查集

目录

• 1. 普通并查集
  • 1. 朴素做法
  • 2. 路径压缩与按秩合并
  • 3. 例题
    • 1. 亲戚（洛谷 P1551 ）
    • 2. 奶酪（NOIP2017 提高组）
    • 3. 猴子
    • 4. Color the Axis（NOI 导刊）
  • 4. 练习
    • 1. 修复公路
    • 2. 朋友圈
    • 3. 程序自动分析
    • 4. Supermarket
    • 5. 星球大战（JSOI）
    • 6. GSS4 - Can you answer these queries IV
    • 7. SUM and REPLACE
    • 8. 白雪皑皑
• 2. 并查集的扩展域（种类并查集）与边带权（带权并查集）
  • 1. 扩展域并查集
  • 2. 边带权并查集
  • 3. 练习
• 3. 可持久化并查集

1. 普通并查集

时间复杂度分析均设 \(n\) 为总元素个数，且为最坏情况下的复杂度 .

1. 朴素做法

并查集（Disjoint Set Union，dsu）是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题 .

具体的，它支持如下操作：

• Find u v：查询元素 \(u,v\) 是否属于同一个集合（查询操作）
• Union u v：合并元素 \(u\) 所属集合与元素 \(v\) 所属集合（合并操作）

并查集的重要思想在于，用集合中的一个元素代表集合 . 即对于每个集合选出一个固定元素作为其「代表元」，这样只需要维护一个「查询某元素所在集合的代表元」操作即可完成上述两操作 .

一个很直接的想法是，维护一个 \(f\)，\(f(x)\) 表示 \(x\) 所在集合的代表元 .
这种做法的 Find 操作的时间复杂度为 \(O(1)\)，Union 操作的时间复杂度为 \(O(n)\) .

另一种思路是使用树形结构（森林），维护一个 \(fa\)，用 \(fa(x)\) 表示 \(x\) 的父亲，特别的，树根的 \(fa\) 值为其本身，用一棵树表示一个集合，这样，合并时只需要找到两个元素的树根 \(r_1,r_2\)，然后执行 \(fa(r_1)\gets r_2\) 即可，查询时只用查询 .
这种做法的 Find 操作与 Union 操作的时间复杂度均为 \(O(n)\)，但是随机数据下是 \(\log\) 的 .

参考代码：

// 因为有意没压行，所以看起来代码较长，实际上则不然

int n; // 元素数量
int fa[N]; // fa 数组 (N 是最大元素数量)
void init() // 初始化每个元素各成一个集合 
{
	for (int i=1;i<=n;i++)
		fa[i]=i; // 每个元素都是它自己的「代表元」，它自己即是树根 
}
int get(int u) // 获取元素 u 所在集合的「代表元」 
{
	if (fa[u]==u) // 是树根，找到了「代表元」
		return u;
	return get(fa[u]);
}
bool find(int u,int v) // 查询操作
{
	return get(u)==get(v);
}
void merge(int u,int v) // 合并操作，union 是 C++ 保留字，故采用 merge
{
	fa[get(u)]=get(v);
}

2. 路径压缩与按秩合并

如何把上面的做法卡成 \(O(n)\)？

用一条链即可，每次对叶节点进行 get 操作就卡掉了

优化！对于每个点 \(u\)，我们查找完它的代表后就记下来！以后就不用重复找了！

这样对于一条长度为 \(L\) 的链，最多只有 \(\dfrac L2\) 次有效操作，加边也只会被一次操作击破，但这样还是 \(O(n)\) 的啊（

但是，发现在递归的时候也经过了路径上的点啊，把路径上的点的代表顺便也记下来就行啦！

int get(int u)
{
	if (fa[u]==u)
		return u;
	return fa[u]=get(fa[u]); // 记下来！
}

这被称为 路径压缩 . 它的时间复杂度是 \(\log\) 级别的，好耶！

读者可能听说过一种叫「启发式合并」的思想，这里也是可以应用的 .

将较小的树合并到较大的树上，深度不变，这减少了查询操作的递归深度，这被称为 按秩合并，在实际操作是把「秩」维护到根上即可 .
同时 使用路径压缩和按秩合并时，Find 操作的时间复杂度为 \(O(\alpha(n))\)，Union 操作的时间复杂度为 \(O(1)\) .

其中 \(\alpha(n)\) 为反阿克曼函数，我们定义阿克曼（Ackermann）函数为

\[A(n)=\begin{cases}n+1&m=0\\A(m-1,1)&m>0,\,n=0\\A(m-1,A(m,n-1))&m>0,\,n>0\end{cases} \]

则反阿克曼函数 \(\alpha(x)\) 定义为最大的使 \(A(t,t)\le x\) 的整数 \(t\)，反阿克曼函数增长极为缓慢，在输入不炸的情况下有 \(\alpha(n)\le 4\) .

注意，单独使用路径压缩的并查集的时间复杂度不是 \(O(\alpha(n))\)，具体证明以及卡法见 时间复杂度-势能分析浅谈 - Atalod，但一般也没人卡，光用路径压缩也没什么问题 .

参考代码略 .

演示：Visualgo 中的并查集可视化（路径压缩+按秩合并）（中文）

3. 例题

注：题目后面的括号里表明了可提交的 OJ . 因为题太老，所以无法确认最初的出题人是谁 .

1. 亲戚（洛谷 P1551 ）

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。

规定：\(x\) 和 \(y\) 是亲戚，\(y\) 和 \(z\) 是亲戚，那么 \(x\) 和 \(z\) 也是亲戚。如果 \(x,y\) 是亲戚，那么 \(x\) 的亲戚都是 \(y\) 的亲戚，\(y\) 的亲戚也都是 \(x\) 的亲戚。

所有人划分到若干个不相交的集合中，每个集合里的人彼此是亲戚。为了判断两个人是否为亲戚，只需看它们是否属于同一个集合即可 . 因此，这里就可以考虑用并查集进行维护了 .

其实类似这样具有传递性的问题几乎都可以用并查集维护 .

2. 奶酪（NOIP2017 提高组）

现有一块大奶酪，它的高度为 \(h\)，它的长度和宽度我们可以认为是无限大的，奶酪中间有许多半径相同的球形空洞。我们可以在这块奶酪中建立空间坐标系，在坐标系中， 奶酪的下表面为 \(z=0\) ，奶酪的上表面为 \(z=h\) 。
现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐标。如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个空洞，特别地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞；如果一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。
位于奶酪下表面的 Jerry 想知道，在 不破坏奶酪 的情况下，能否利用已有的空洞跑到奶酪的上表面去?
空间内两点 \(P_1(x_1,y_1,z_1)\)、\(P_2(x_2,y_2,z_2)\) 的距离公式如下：

\[\mathrm{dist}(P_1P_2)D\sqrt{(x_1-x_2)^2(y_1-y_2)^2(z_1-z_2)^2} \]

两个空洞或若能互相到达（相交或相切）就将它们合并到同一个集合，也得维护特殊元素顶部和底部，合并类似 .

最后看顶部和底部是不是在同一个集合中即可判定，图解：

3. 猴子

有 \(n\) 只猴子，第一只尾巴挂在树上，剩下的 \(n-1\) 只，要么被其他的猴子抓住，要么抓住了其他的猴子，要么两者均有。当然一只猴子最多抓两只另外的猴子。现在给出这 \(n\) 只猴子抓与被抓的信息，并且在某个时刻可能某只猴子会放掉它其中一只手的猴子，导致某些猴子落地。求每只猴子落地的时间。

反向处理询问，把松手变成牵手，并查集维护即可（维护是否与第一只挂在树上的猴子连通）

4. Color the Axis（NOI 导刊）

在一条数轴上有 \(n\) 个点，分别是 \(1,2,\ldots,n\) . 一开始所有的点都被染成黑色。接着我们进行 \(m\) 次操作，第 \(i\) 次操作将 \([l_i,r_i]\) 这些点染成白色 . 请输出每个操作执行后剩余黑色点的个数 .

一眼线段树，线段树也确实能过，，，

但是，线段树的题怎么能用线段树做呢？

考虑暴力，并用并查集维护一些已经赋为 \(0\) 的段，并查集的代表元素选为段的最末尾一个元素，每次直接 get(l) 跳到段尾，然后合并来表示赋 \(0\) .

这个算法的时间复杂度是 \(O((n+m)\alpha(n))\)，比线段树优秀，证明见 此处 .

4. 练习

1. 修复公路

A 地区在地震过后，连接所有村庄的公路都造成了损坏而无法通车。政府派人修复这些公路。

给出 A 地区的村庄数 \(n\)，和公路数 \(m\)，公路是双向的。并告诉你每条公路的连着哪两个村庄，并告诉你什么时候能修完这条公路。问最早什么时候任意两个村庄能够通车，即最早什么时候任意两条村庄都存在至少一条修复完成的道路（可以由多条公路连成一条道路）

题目链接：https://www.luogu.com.cn/problem/P1111

提示

可以用并查集维护村庄的联通（即通车）哦

2. 朋友圈

班上有 \(n\) 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。
给定一个 \(n\times n\) 的矩阵 \(M\)，表示班级中学生之间的朋友关系。如果 \(M_{i,j}=1\)，表示已知第 \(i\) 个和 \(j\) 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

题目链接：https://leetcode-cn.com/problems/friend-circles/

提示

用并查集维护朋友圈后，寻找父亲可以直接用 fa[i]=i 判断

3. 程序自动分析

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足 .

考虑一个约束满足问题的简化版本：假设 \(x_1,x_2,x_3,\cdots\) 代表程序中出现的变量，给定 \(n\) 个形如 \(x_i=x_j\) 或 \(x_j\neq x_j\) 的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：\(x_1=x_2,x_2=x_3,x_3=x_4,x_4\neq x_1\)，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足 .

现在给出一些约束满足问题，请分别对它们进行判定 .

题目链接：https://www.luogu.com.cn/problem/P1955

提示1

不等关系是没有传递性的哦

提示2

可以考虑离线先处理所有等于关系，再判断不等于是否成立

4. Supermarket

给定 \(n\) 个商品，每个商品有利润 \(p_i\) 和过期时间 \(p_i\)，每天只能卖一个商品，过期了的商品不能卖 .

问：如何安排每天卖的商品，使总收益最大？

题目链接：https://vjudge.net/problem/POJ-1456
（当然这题可以反悔贪心，但是这里要求一个并查集做法）

提示1

有一种显而易见的贪心策略：优先卖出利润大的商品，每个商品再过期之前尽量晚卖出 .

提示2

维护一个关于「天数」的并查集，起初每个商品各成集合，对于每个商品，若它在 d 天后过期，则查询其所在集合的树根 r，若 r>0，则把它安排在第 t 天卖，并令 r 为 r-1 的子节点
这其实就是维护了一个数组中的空闲位置，然后找最晚时间尽量放

5. 星球大战（JSOI）

有一张无向图，\(k\) 次操作，每次删掉一个给定点和所有和其连接的边，求每次操作后图的连通块个数

题目链接：https://www.luogu.com.cn/problem/P1955

提示1

类似 猴子 那题，把删点变成加点

提示2

每次加点可以看做对于这个点加上所有原有的边，并查集维护即可

6. GSS4 - Can you answer these queries IV

维护一个数据结构（序列上），支持区间开方（下取整），区间和 .

题目链接：https://www.spoj.com/problems/GSS4/ or https://www.luogu.com.cn/problem/P4145

提示1

每一个数其实并不会有太多次「有用开方」，每个数其实经过几次开方就变成 1 了（注：1e18 经过 6 次开方即变成 1）

提示2

类似 Color the Axis 那题，用并查集维护每个点是否该不用再替换（为 1）即可

7. SUM and REPLACE

有一个长度为 \(n\) 的序列，要求支持以下两种操作：

• 将 \(l\le i\le r\) 中所有 \(a_i\) 替换成 \(d(a_i)\)，其中 \(d(t)\) 是 \(t\) 的正约数个数 .
• 求 \(\sum\limits_{i=l}^ra_i\) .

题目链接：http://codeforces.com/problemset/problem/920/F

提示1

d(t)=O(sqrt t)

提示2

和上一题基本相同 .

8. 白雪皑皑

现在有 \(n\) 片雪花排成一列 . Pty 要对雪花进行 \(m\) 次染色操作，第 \(i\) 次染色操作中，把第 \((ip+q)\bmod n+1\) 片雪花和第 \((iq+p)\bmod n+1\) 雪花之间的雪花（包括端点）染成颜色 \(i\) . 其中 \(p,q\) 是给定的两个正整数。他想知道最后 \(n\) 片雪花被染成了什么颜色 .

（注：这里先算 \(\bmod n\) 再算 \(+1\)）
题目链接：https://www.luogu.com.cn/problem/P2391

提示1

因为后面的修改会覆盖前面的，所有先将修改反向，使前面的染色点不能覆盖后面的染色点保证最后修改的不被覆盖

提示2

需要快速查找下一个没被涂的点，用并查集维护即可

2. 并查集的扩展域（种类并查集）与边带权（带权并查集）

1. 扩展域并查集

一般的并查集，维护的是具有连通性、传递性的关系，例如亲戚的亲戚是亲戚 . 但是，有时我们要维护另一种关系：敌人的敌人是朋友 . 扩展域并查集就是为了解决这个问题而诞生的 .

我们由一道例题引入：

团体（BOI2003）

给定 \(n\) 个人，他们之间有两种关系，朋友与敌对 . 可以肯定的是：

• 与我的朋友是朋友的人是我的朋友
• 与我敌对的人有敌对关系的人是我的朋友

现在这 \(n\) 个人进行组团，两个人在一个团队内当且仅当他们是朋友 .

求最多的团体数 .

我们开一个两倍大小的并查集 . 例如，假如我们要维护 \(4\) 个元素的并查集，我们改为开 \(8\) 个单位的空间：

我们用蓝色维护朋友关系，用橙色维护敌人关系 .

如果说有 \(u,v\) 是朋友，则在蓝色中连接 \(u,v\)，这是平凡的

如果说有 \(u,v\) 是敌人，则在连接 \(u,v+4\) 与 \(u+4,v\)，也就是相当于蓝橙直接跨越颜色的是敌人，这样刚好满足「敌人的敌人是朋友」（跨两次跨回来了）.

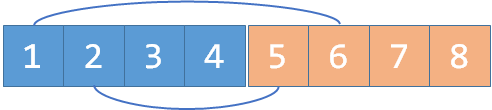
同样，我们也可以不止用二倍空间：

食物链（NOI2001）

动物王国中有三类动物 A,B,C，这三类动物的食物链构成了有趣的环形 . A 吃 B，B 吃 C，C 吃 A .

现有 \(n\) 个动物，以 \(1,2,3,\cdots n\) 编号 . 每个动物都是 A,B,C 中的一种，但是我们并不知道它到底是哪一种

有人用两种说法对这 \(n\) 个动物所构成的食物链关系进行描述：

• 第一种说法是 1 X Y，表示 X 和 Y 是同类 .
• 第二种说法是2 X Y，表示 X 吃 Y .

此人对 \(n\) 个动物，用上述两种说法，一句接一句地说出 \(k\) 句话，这 \(k\) 句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话 .

• 当前的话与前面的某些真的话冲突，就是假话 .
• 当前的话中 X 或 Y 比 \(n\) 大，就是假话 .
• 当前的话表示 X 吃 X，就是假话 .

你的任务是根据给定的 \(n\) 和 \(k\) 句话，输出假话的总数 .

用三倍空间，分别维护 同类，吃，被吃 三种关系即可 .

关键代码：

int main()
{
	scanf("%d%d",&n,&k); bc::init();
	for (int i=0,opt,x,y;i<k;i++)
	{
		scanf("%d%d%d",&opt,&x,&y);
		if ((x>n)||(y>n)){++fake; continue;}
		if (opt==1)
		{
			if (same(x,y+n)||same(y,x+n)){++fake; continue;}
			merge(x,y); merge(x+n,y+n); merge(x+2*n,y+2*n);
		}
		else
		{
			if (x==y){++fake; continue;}
			if (same(x,y)||(same(y+2*n,x))){++fake; continue;}
			merge(x,y+n); merge(x+n,y+2*n); merge(x+2*n,y);
		}
	} printf("%d",fake);
	return 0;
}

2. 边带权并查集

因为并查集的结构其实是森林，我们可以在每条边上记录权值 .

即维护一个数组 \(d\)，用 \(d(x)\) 保存节点 \(x\) 到父节点之间的边权，路径压缩以后，每个访问过的节点都会直接指向树根，如果我们同时更新它们，就可以统计它们到树根的路径上的一些信息 .

这就是「边带权」并查集，描述可能有点抽象，下面用一道例题来具体说明 .

银河英雄传说（NOI2002）

有一个划分成 \(n\) 列的星级战场，编号为 \(1,2,\cdots,n\) . 有 \(n\) 艘战舰，编号为 \(1,2,\cdots,n\)，初始第 \(i\) 个战舰处于第 \(i\) 列 .

有两种操作：

• M i j，直接把第 \(i\) 列战舰接到第 \(j\) 列战舰后面 .
• C i j，查询第 \(i\) 个战舰和第 \(j\) 个战舰是否在同一列，如果在，询问之间隔了多少个战舰 .

显然可以把每一列上的战舰用并查集维护 .

让树上每条边都带权值 \(1\) 即可，路径压缩需要微调一下，代码见下：

int get(int x)
{
    if (x==fa(x)) return x;
    int root=get(fa[x]); // 获取根节点！
    d[x]+=d[fa[x]]; // 加上父亲节点的权值
    return fa[x]=root; // 最后再路径压缩
}

这里需要记录一个集合大小数组 \(size\)，以便合并：

void merge(int x,int y)
{
    x=get(x); y=get(y); // 每个元素变成对应代表元
    fa[x]=y; // 朴素合并
    d[x]=size[y]; // 注意这里根节点是没有权的，这里记上大小是说明把它加入进去了，在路径压缩的时候就会更新它的孩子了，显然这样不会出现错误
    size[y]+=size[x]; // 别忘了 size 也要更新
}

应该还是挺好理解的嘛 .

边带权并查集其实就是维护了每个节点到根节点的权值「和」（这里不一定是 \(+\)，可能是异或 \(\oplus\)，乘积 \(\times\)，最大公约数 \(\gcd\) 等）

Parity Game

有一个 01 序列 \(S\)，有 \(n\) 次回答分别表示 \(S_l,S_{l+1},\cdots,S_r\) 有奇数个 \(1\) 还是偶数个 \(1\) .

求一个最小的 \(k\)，使得 存在 序列 \(S\) 使得其满足第 \(1\sim k\) 个回答，但不满足第 \(1\sim k+1\) 个回答 .

先做前缀和

\[sum_i=\sum_{i=1}^nS_i \]

可以递推维护，然后因为

• \(l\sim r\) 有偶数个 \(1\) 等价于 \(sum_{l-1}\) 和 \(sum_r\) 奇偶性不同
• \(l\sim r\) 有偶数个 \(1\) 等价于 \(sum_{l-1}\) 和 \(sum_r\) 奇偶性相同

常见的，这种奇偶性的传递可以 \(\bmod 2\) 做加法解决，也就是异或（xor）运算 .

令 \(d(x)=(x-fa(x))\bmod 2\)，每次合并时由原来的 \(+\) 变成异或即可维护奇偶性的变化 .

这里的合并比较特殊，但是也不难 .

合并 \(x\) 与 \(y\)，显然只需对 \(d(x),d(y)\) 和询问的答案做不进位加法即可，这相当于把 \(x\) 到 \(y\) 这一段路程拆成三份处理了，然后运用异或的逆运算是异或，即可得解 . 具体的，过程如下

合并时，设 \(x,y\) 的代表元分别是 \(r_x,r_y\)，考虑 \(x\sim y\) 的奇偶性怎么算 .

\(x\sim y\) 这一段可以拆为 \(x\sim r_1,r_1\sim r_2,r_2\sim y\) .

于是答案 \(t\) 即为 \(d(x)\oplus d(p\,或\,q)\oplus d(y)\)，其中 \(\oplus\) 是异或运算 .

从而易见 \(d(p\,或\,q)=d(x)\oplus d(y)\oplus t\) .

一般大部分问题都是可以用边带权并查集解也可以用扩展域并查集解的，上面那题就可以用扩展域记录奇数域与偶数域 .

旧题「食物链」也可以在 \(\bmod 3\) 意义下做边带权 .

3. 练习

略！！！好耶！！！！！！！！

3. 可持久化并查集

咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕咕