qbxt五一数学Day2

1. 判断素数（素性测试）

1. \(O(\sqrt n)\) 试除

bool isprime(int n)
{
	if (n<2) return false;
	for (int i=2;i*i<=n;i++)
		if (!(n%i)) return false;
	return true;
}

2. Miller-Rabin 素性测试

Theorm 1

若 \(n\) 是素数，则对于任意 \(1\le a\le n\)，设 \(n-1=d\cdot 2^r\)，则

\[a^d\equiv 1\pmod n\;,\;{\large \exists}_{0\le i\le r}\,a^{d\cdot 2^i}\equiv -1\pmod n \]
中至少有一个成立 .

随便找若干个数 \(a\) 进行判定，很大概率对（4~8 个在 long long 范围稳了）（取质数效果较好）

时间复杂度 \(O(k\log^2 n)\)

const int PrimeList[]={2,3,5,11,37,43,67,73,97}; // for Miller-Rabin
ll qmul(ll a,ll n,ll P)
{
	ll ans=0; if (!n) return 0;
	while (n)
	{
		if (n&1) ans=(ans+a)%P;
    	n>>=1; a=(a+a)%P;
	} return ans%P;
}
ll qpow(ll a,ll n,ll P)
{
	ll ans=1;
	while (n)
	{
		if (n&1) ans=qmul(ans,a,P)%P;
		n>>=1; a=qmul(a,a,P)%P;
	} return ans;
}
bool miller_rabin(ll n,int a)
{
	ll d=n-1,r=0;
	while (!(d&1)){++r; d>>=1;}
	ll x=qpow(a,d,n);
	if (x==1) return true;
	for (int i=0;i<r;i++)
	{
		if (x==n-1) return true;
		x=qmul(x,x,n)%n;
	} return false;
}
bool MillerRabin(ll n)
{
	if (n<2) return false;
	for (int i=0;i<9;i++)
	{
		if (n==PrimeList[i]) return true;
		if (n%PrimeList[i]==0) return false;
		if (!miller_rabin(n,PrimeList[i])) return false;
	} return true;
}

* 欧拉函数

定义：

\(\varphi(n)\) 定义为 \(1\sim n\) 中与 \(n\) 互质的数的个数，即：

\[\varphi(n)=\sum_{i=1}^n[\gcd(i,n)=1] \]

Theorm *

欧拉函数的求值公式：

\[\varphi(n)=n\left(1-\dfrac 1{p_1}\right)\left(1-\dfrac 1{p_2}\right)\cdots\left(1-\dfrac 1{p_r}\right)\mathrm{\,where\;} n=\prod_{i=1}^r p_i^{\alpha_i} \]

Proof：容斥原理

\[\tag*{□} \]

公式求 \(\varphi\) 值：

ll phi(ll n) // O(sqrt(n))
{
	ll ans=n;
	for (int i=2;i*i<=n;i++)
		if (!(n%i))
		{
			ans=ans/i*(i-1);
			while (!(n%i)) n/=i;
		}
	if (n>1) ans=ans/n*(n-1);
	return ans;
}

Theorm *（欧拉函数是积性函数）

若 \(n,m\) 互质，则 \(\varphi(n)\varphi(m)=\varphi(nm)\) .

Proof：由求值式子显然得证 .

\[\tag*{□} \]

2. 逆元

定义：

若 \(b\) 使得 \(ab\equiv 1\pmod m\)，则 \(b\) 成为 \(a\) 模 \(m\) 意义下的逆元，记作 \(b=a^{-1}\) .

Theorm 2
逆元存在的充要条件是 \(\gcd(a,m)=1\) .

我们知道费马小定理和欧拉定理：

Theorm 3（费马小定理）

对于 \(\gcd(a,p)=1\) 且 \(p\) 为质数，有：

\[a^{p-1}\equiv 1\pmod p \]

Theorm 4（欧拉定理）

对于 \(\gcd(a,p)=1\)，有：

\[a^{\varphi(p)}\equiv 1\pmod p \]
其中 \(\varphi\) 是欧拉函数 .

素数求逆元：用费马小定理，答案是 \(a^{-1}=a^{p-2}\) .

其他：

用欧拉定理，答案是 \(a^{-1}=a^{\varphi(p)-1}\) .
用 exgcd，问题等价于求解 \(ax+by=p\) .

求 \(1\sim n\) 的逆元：

预处理阶乘，阶乘逆元可以

\[(n-1)!^{-1}=n!^{-1}n \]

求，\(n\) 的逆元可以

\[n^{-1}=n!^{-1}(n-1)! \]

求 .

3. exgcd（扩展欧几里得）

求解不定方程

\[ax+by=c \]

其中 \(x,y\) 是整数 .

Theorm 5（裴蜀定理 / 贝祖定理）

\[ax+by=c \]
有解当且仅当 \(\gcd(a,b)\mid c\) .

所以只需要处理 \(ax+by=\gcd(a,b)\) 的解即可 .

注意到 \(\gcd(a,b)=\gcd(b,a\bmod b)\)，设 \(G=\gcd(a,b)\) .

我们按照欧几里德算法（即辗转相除法），当 \(b=0\) 时，容易发现 \(x=1,y=0\) .

若不然，如果我们知道

\[bx_0+(a\bmod b)y_0=G \]

的解，我们就可以依照如下方法求 \(ax+by=G\) 的解：

\[\begin{aligned}bx_0+(a\bmod b)y_0&=bx_0+\left(a-b\left\lfloor\dfrac ab\right\rfloor\right)y_0\\&=ay_0+b\left(x_0-y_0\left\lfloor\dfrac ab\right\rfloor\right)\end{aligned} \]

int ex_gcd(int a,int b,int& x,int& y)
{
	if (!b){x=1; y=0; return a;}
	int xp,yp,g=ex_gcd(b,a%b,xp,yp);
	x=yp; y=xp-yp*(a/b); return g;
	return 0;
}

4. 离散对数（BSGS 算法求解）

BSGS：大步小步算法~~北上广深·百事公司·阿姆斯特朗算法~~

求解同余方程

\[a^x\equiv b\pmod p \]

其中 \(p\) 是质数 .

由费马小定理，这个 \(x\) 不会超过 \(p-1\) .

分成如下数表：

如图，将所有行转换到第一行，用一个 set 或 hash 维护即可 .

ll BSGS(ll a,ll b,ll p) // a^x=b (mod p)
{
	int s=sqrt(p),x=1; set<int> se;
	for (int i=0;i<s;i++){se.insert(x); x=1ll*x*a%p;}
	int y=qpow(qpow(a,s,p),p-2,p),z=b;
	for (int i=1;;i++)
	{
		if (se.count(z))
		{
			z=qpow(a,(i-1)*s,p);
			for (int j=(i-1)*s;;j++)
				if (z==b) return j;
				else z=1ll*z*a%p;
		} z=1ll*z*y%p;
	}
} // 要判无解只需要判断循环次数是否过多即可 .

5. CRT（中国剩余定理）

考虑合并两个方程，

\[\begin{cases}x\equiv b_1\pmod{p_1}\\x\equiv b_2\pmod{p_2}\end{cases} \]

法一：大数翻倍法（zhx 的神仙解法）

枚举 \(b_1,b_1+p_1,b_1+2p_1,\cdots\) 判断是否成立

static pair<ll,ll> MergeEqu(ll a1,ll m1,ll a2,ll m2)
{
	if (m2>m1) swap(m1,m2),swap(a1,a2);
	while (a1%m2!=a2) a1+=m1;
	return make_pair(a1,lcm(m1,m2));
}

法二：用扩展欧几里得解

令 \(x=k_1p_1+b_1=k_2p_2+b_2\)，则

\[k_1p_1-k_2p_2=b_2-b_1 \]

则：

\[\dfrac{k_1p_1}{\gcd(p_1,p_2)}\equiv \dfrac{b_2-b_1}{\gcd(p_1,p_2)}\left(\bmod {\dfrac{p_2}{\gcd(p_1,p_2)}}\right) \]

用扩欧解出 \(k_1\) 即可 .

6. 线性筛（xxs）

1. 筛素数

~~碍事筛~~埃氏筛：

notprime[1]=true;
for (int i=2;i<=n;i++)
{
	if (notprime[i]) continue;
	for (int j=i+i;j<=n;j++) notprime[j]=true;
}

这是对于每个素数 \(i\) 枚举它的所有倍数筛掉

我们反过来，用每个数 \(i\) 枚举它的所有素数倍：

vector<int> plist; notprime[1]=true;
for (int i=2;i<=n;i++)
{
	if (!notprime[i]) plist.push_back(i);
	for (auto x:plist)
	{
		int now=i*x;
		if (now>n) break;
		notprime[x]=true;
	}
} // C++11

/* 数组写法  */

notprime[1]=true;
for (int i=2;i<=n;i++)
{
	if (!notprime[i]) plist[++pcnt]=i;
	for (int j=1;j<=pcnt;j++)
	{
		int now=i*plist[j];
		if (now>n) break;
		notprime[plist[j]]=true;
	}
}

注意到每个数可能被筛多次，例如：

\[12=2\times 6=3\times 4 \]

翻过来后就是枚举到 \(4,6\) 时，找到 \(2,3\) 筛掉 \(12\) .

我们希望每个数只被它的最小质因子筛掉 .

我们进行模拟：

当我们发现 \(4\) 时，枚举：

素数 \(2\)：筛掉 \(8\) .
素数 \(3\)：注意到 \(2\)（上一个素数）是 \(4\) 的倍数，所以后面的素数都不用枚举了，因为不是最小素因子（此处最小素因子至多是 \(2\)）

用这种想法写出最终代码：

vector<int> plist; notprime[1]=true;
for (int i=2;i<=n;i++)
{
	if (!notprime[i]) plist.push_back(i);
	for (auto x:plist)
	{
		int now=i*x;
		if (now>n) break;
		notprime[x]=true;
		if (!(i%x)) break;
	}
}

2. 筛积性函数（\(\varphi\)，\(\mu\)）

当 \(k\) 是素数时：

\[\varphi(k)=k-1\;,\;\mu(k)=-1 \]

当第 \(10\) 行成立，显然 \(\mu(now)=0\) .

因为没有其他增加的素因子，由欧拉函数计算式得 \(\varphi(now)=x\cdot\varphi(x)\) .

如果互素（即第 \(11\) 行成立），由积性显然有 \(\varphi(now)=\varphi(x)\varphi(i)\)，\(\mu(now)=\mu(x)\mu(i)\)

在板子上改一改就行辣

notprime[1]=true; phi[1]=mu[1]=1;
for (int i=2;i<=n;i++)
{
	if (!notprime[i]){plist.push_back(i); phi[i]=i-1; mu[i]=-1;}
	for (auto x:plist)
	{
		int now=i*x;
		if (now>n) break;
		notprime[now]=true;
		if (!(i%x)){phi[now]=phi[i]*x; mu[now]=0; break;}
		else{phi[now]=phi[i]*phi[x]; mu[now]=mu[i]*mu[x];}
	}
}

7. 数论函数与狄利克雷卷积

1. \(\mu\)

1. 定义与性质

\(\mu\)：莫比乌斯函数，数论容斥函数 .

定义：

对于整数 \(n\)，定义：

\[\mu(n)=\begin{cases}1&n=1\\(-1)^r&{\large\forall}_{i\in[1,r]\cap \mathbb Z}:\alpha_i=1\\0&\rm otherwise.\end{cases}\mathrm{\,where\;} n=\prod_{i=1}^r p_i^{\alpha_i} \]

Theorm：对于 \(n\perp m\)，有 \(\mu(nm)=\mu(n)\mu(m)\)（\(\mu\) 是积性函数 .

Proof：

设

\[n=\prod_{i=1}^r p_i^{\alpha_i}\;,\;m=\prod_{i=1}^t q_i^{\beta_i} \]

其中 \({\large \forall}_{i\in[1,r]\cap \mathbb Z\,,\,j\in[1,t]\cap \mathbb Z}:p_i\neq q_j\)（即 \(n,m\) 互质）.

当 \(\alpha_i=\beta_j=1\) 时（其余情况易证），

\[\mu(nm)=\mu\left(\prod_{i=1}^r p_i^{\alpha_i}\cdot \prod_{i=1}^t q_i^{\beta_i}\right)=(-1)^{r+t}=(-1)^r(-1)^t=\mu(n)\mu(m)\tag*{⬜} \]

2. 例题

问在 \(1\) 到 \(n\) 中有多少个数可以表示为

\[t=x^y \]
其中 \(x\ge 1,y\ge 2\) .
数据范围：\(n\le 10^{18}\)

对于对于一个 \(y\)，存在 \(\sqrt[y]n\) 个 \(x\) 满足条件（显然有 \(y\le \log_2 (10^{18})\)，即 \(y\le 64\)）.

注意到有数会重复，e.g.

\[64=8^2=4^3=2^6 \]

答案即为：

\[\sum_{i=2}^{64}-\mu(i)(\sqrt[i]n-1)+1 \]

（这个 \(-1\) \(+1\) 是为了去掉 \(1=1^?\)）
暴力求即可 .

2. 狄利克雷卷积

1. 定义

数论卷积（或狄利克雷（Dirichlet）卷积）：

对于数论函数 \(f,g\)，定义他们的狄利克雷卷积为：

\[(f*g)(n)=\sum_{d\mid n}f(d)g\left(\dfrac nd\right) \]
注：\(\sum\limits_{d\mid n}\) 是枚举因子 .

有性质：

交换律：\(f*g=g*f\) .
结合律：\((f*g)*h=f*(g*h)\)
分配律：\((f+g)*h=f*h+g*h\)

2. 特殊函数的狄利克雷卷积

一

\[\mu*I=\varepsilon \]

其中 \(I(n)=1\,,\,\varepsilon(n)=[n=1]\) .

即对于 \(n>1\)，有：

\[\sum_{d\mid n}\mu(d)=0 \]

二

\[\varphi*I=id \]

其中 \(id(n)=n\) .

即：

\[\sum_{d\mid n}\varphi(d)=n \]

三

\[\mu*id=\varphi \]

Proof：

\[\begin{aligned}\mu* id&=\mu*\varphi*I\\&=\mu*I*\varphi\\&=\varepsilon*\varphi\\&=\varphi\end{aligned} \]

3. 例题

求和变形技巧：

增加枚举变量
交换枚举顺序
删除无用变量

Problem 1

给定 \(n,m\)，求：

\[\sum_{i=1}^n\sum_{j=1}^m\gcd(i,j) \]

\[\begin{aligned}\sum_{i=1}^n\sum_{j=1}^m\gcd(i,j)&=\sum_{i=1}^n\sum_{j=1}^mid(\gcd(i,j))\\&=\sum_{i=1}^n\sum_{j=1}^m\sum_{d\mid\gcd(i,j)}\varphi(d)&\text{（增加枚举变量）}\\&=\sum_{d=1}^n\sum_{i=1}^{\left\lfloor\frac nd\right\rfloor}\sum_{i=1}^{\left\lfloor\frac md\right\rfloor}\varphi(d)&\text{（交换枚举顺序）}\\&=\sum_{d=1}^n\left\lfloor\dfrac nd\right\rfloor\left\lfloor\dfrac md\right\rfloor\varphi(d)&\text{（删除无用变量）}\end{aligned} \]

（第三个等号是把 \(\gcd\) 转换成枚举倍数）.

然后预处理 \(\varphi\)，时间复杂度 \(O(n)\) .

Problem 2

给定 \(n\)，问存在多少 \(1\le i,j\le n\)，使得 \(i,j\) 互质 .

显然题目让求的是：

\[\begin{aligned}\sum_{i=1}^n\sum_{j=1}^n\varepsilon(\gcd(i,j))&=\sum_{i=1}^n\sum_{j=1}^m\sum_{d\mid\gcd(i,j)}\mu(d)&\text{（增加枚举变量）}\\&=\sum_{d=1}^n\sum_{i=1}^{\left\lfloor\frac nd\right\rfloor}\sum_{i=1}^{\left\lfloor\frac md\right\rfloor}\mu(d)&\text{（交换枚举顺序）}\\&=\sum_{d=1}^n\left\lfloor\dfrac nd\right\rfloor\left\lfloor\dfrac md\right\rfloor\mu(d)&\text{（删除无用变量）}\end{aligned} \]

和上一题几乎一样 [表情]

3. 莫比乌斯反演

\[g(n)=\sum_{d\mid n}f(d)\;\Leftrightarrow\;f(x)=\sum_{d\mid n}\mu(d)g\left(\dfrac nd\right) \]
即

\[g=f*I\;\Leftrightarrow\;f=\mu*g \]

Proof：

\[\begin{aligned}g=f*I&\Leftrightarrow \mu*g=f*I*\mu\\&\Leftrightarrow \mu*g=f*\varepsilon\\&\Leftrightarrow \mu*g=f\end{aligned} \]

\[\tag*{⬜} \]

8. 计数

1. 计数原理

1. 加法原理

一件事若干类（并列），方案数加起来

2. 乘法原理

一件事若干步（递进），方案数乘起来

2. 排列组合

定义

组合：\(n\) 中无序选 \(r\)：

\[C(n,r)=\dbinom{n}{r}=\dfrac{n!}{r!(n-r)!} \]

排列：\(n\) 中有序选 \(r\)：

\[P(n,r)=A(n,r)=n^{\underline{r}}=\dfrac{n!}{(n-r)!} \]

性质

\[\dbinom{n+m}{n}=\dbinom{n+m}{m} \]

组合意义：选不选的

\[\dbinom{n}{m}=\dbinom{n-1}{m-1}+\dbinom{n-1}{m} \]

组合意义：第一件选不选

\[\dbinom{n+r+1}{r}=\dbinom{n+r}{r}+\dbinom{n+r-1}{r-1}+\cdots+\dbinom{n}{0}=\sum_{i=0}^r\dbinom{n-r-i}{r-i} \]

反复用前面那个式子

\[\dbinom{n}{l}\dbinom{l}{r}=\dbinom{n}{r}\dbinom{n-r}{l-r} \]

组合意义：选两次

\[\dbinom{n}{0}+\dbinom{n}{1}+\cdots+\dbinom{n}{n}=2^n \]

组合意义：取数用乘法原理、组合数两种算法

\[\dbinom{n}{0}-\dbinom{n}{1}+\dbinom{n}{2}-\cdots=0 \]

组合意义：建立奇数项与偶数项的一一对应，以达成消去的效果（第一项取反） .

\[\dbinom{r}{r}+\dbinom{r+1}{r}+\cdots+\dbinom{n}{r}=\dbinom{n+1}{r+1} \]

qwq

\[(1+x)^n=\sum_{k=0}^n\dbinom{n}{k}x^{n-k}=\sum_{k=0}^n\dbinom{n}{k}x^{k} \]

（二项式定理）

组合意义：多项式乘法选数 .

几道小题

Problem 1

\(n\) 里选 \(k\) 数，数字可以相同，求方案数.

一个独特的解法：设选 \(a_1\le a_2\le \cdots\le a_k\) .
构造 \(g_1=a_1,g_2=a_2+1,g_3=a_3+2,\cdots\)，然后对 \(g\) 作组合，得答案为

\[\dbinom{n+k-1}{k} \]

Problem 2

\(n\) 里选 \(k\) 数，数字不能相邻，求方案数.

类似的设选 \(a_1< a_2< \cdots< a_k\) .
构造 \(g_1=a_1,g_2=a_2-1,g_3=a_3-2,\cdots\)，然后对 \(g\) 作组合，得答案为

\[\dbinom{n-k+1}{k} \]

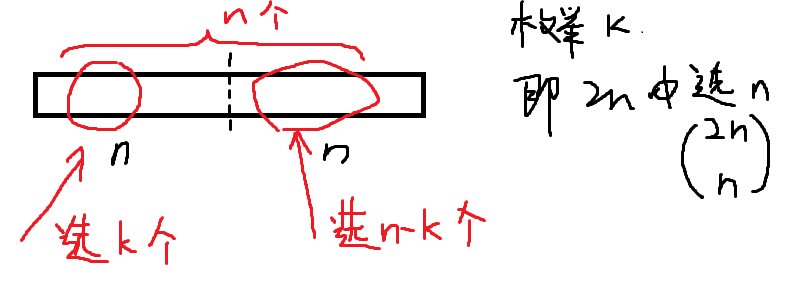
Problem 3

计算

\[\sum_{k=1}^n \dbinom{n}{k}^2 \]

\[\begin{aligned}\sum_{k=1}^n \dbinom{n}{k}^2&=\sum_k\dbinom{n}{k}\dbinom{n}{n-k}\\&=\dbinom{2n}{n}\end{aligned} \]

第二个等号用组合意义：

posted @ 2021-05-02 18:39 Jijidawang 阅读(112) 评论(1) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

Jijidawang

qbxt五一数学Day2

1. 判断素数（素性测试）

1. \(O(\sqrt n)\) 试除

2. Miller-Rabin 素性测试

* 欧拉函数

2. 逆元

3. exgcd（扩展欧几里得）

4. 离散对数（BSGS 算法求解）

5. CRT（中国剩余定理）

法一：大数翻倍法（zhx 的神仙解法）

法二：用扩展欧几里得解

6. 线性筛（xxs）

1. 筛素数

2. 筛积性函数（\(\varphi\)，\(\mu\)）

7. 数论函数与狄利克雷卷积

1. \(\mu\)

1. 定义与性质

2. 例题

2. 狄利克雷卷积

1. 定义

2. 特殊函数的狄利克雷卷积

一

二

三

3. 例题

Problem 1

Problem 2

3. 莫比乌斯反演

8. 计数

1. 计数原理

1. 加法原理

2. 乘法原理

2. 排列组合

定义

性质

几道小题

Problem 1

Problem 2

Problem 3

公告