浅谈拉格朗日插值

目录

• 1. 多项式插值定理
• 2. 插值方法
  • 0. 暴力（Get 0 Points）插值
  • 1. 拉格朗日（Lagrange）插值
    • 1. 朴素做法
    • 2. 当 $x_i$ 连续时的更优做法
    • 3. 重心拉格朗日插值
• 3. 快速插值
  • 1. $O(n\log^3 n)$ 插值
  • 2. $O(n^2\log^2 n)$ 插值
  • 3. $O(n\log^2 n)$ 插值
• 4. 一些例题
  • 1. 自然数 $k$ 次方和
• *. 有关定理的证明
  • 1. 多项式插值定理
  • 2. 多项式插值误差定理

1. 多项式插值定理

我们知道，两点可以确定一条直线（一次多项式），而三点可以确定一条二次函数，四点可以确定一个三次函数 ......

这不由得让我们产生思考——给定 $n+1$ 个点，是否有一个唯一的 $n$ 次多项式过这所有点呢？答案是肯定的，这个定理被称作 多项式插值定理，证明见 * 一节 .

注意做题时必须确定答案是多项式才能插值，比如对非常平稳的一组点做插值时：

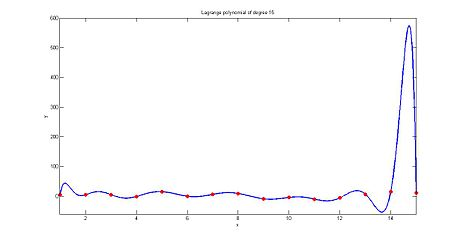
，，，，，，，，，，[表情]

2. 插值方法

由于多项式插值定理的存在，我们下面研究一个问题：给定 $n+1$ 个点 $(x_0,y_0),(x_1,y_1),\cdots,(x_n,y_n)$，求一个多项式 $f(x)$ 使得 $f(x_i)=y_i)$ .

0. 暴力（Get 0 Points）插值

和多项式插值定理的证明差不多，高斯消元解方程组即可，时间复杂度 $O(n^3)$ .

当然也可以用 Cramer 法则求出解的表达式然后解行列式，也是 $O(n^3)$ 的，但是常数会高一些

1. 拉格朗日（Lagrange）插值

1. 朴素做法

考虑构造 $n+1$ 个多项式 $g_i(x)$，使得 $g_i(x_i)=y_i$，且对于任意 $i\neq j$ 有 $g_i(x_j)=0$，然后 $\sum\limits_{i=0}^n g_i(x)$ 即是所求多项式 .

构造这个 $g_i$，可以令 $g_i(x)=y_i\ell_i(x)$，这样 $\ell_i(x)$ 只取 $\{0,1\}$，那么自然满足条件 .

令 $\ell_i(x)$ 为

$$\ell_i(x) = \prod_{i\neq j}\dfrac{x-x_j}{x_i-x_j}$$

即可，当 $x=x_i$ 时，每项都是 $\dfrac{x_i-x_j}{x_i-x_j}=1$，当 $x\neq x_i$ 时，一定有一项使得分子为 $0$ .

所以我们就得到了拉格朗日插值公式：

$$L_n(x)=\sum_{i=0}^ny_i\prod_{i\neq j}\dfrac{x-x_j}{x_i-x_j}$$

上面设的 $\ell_i(x)$ 称做拉格朗日基本多项式（插值基函数），$L_n(x)$ 叫做拉格朗日插值多项式 .

下面给出模板题 洛谷 P4781 的代码：

ll ans=0,x[N],y[N];
int n,k;
ll qpow(ll a,ll n)
{
	ll ans=1;
	while (n)
	{
		if (n&1) ans=ans*a%MOD;
		a=a*a%MOD; n>>=1;
	} return ans%MOD;
}
int main()
{
	scanf("%d%d",&n,&k);
	for (int i=1;i<=n;i++) scanf("%lld%lld",x+i,y+i);
	for (int i=1;i<=n;i++)
	{
		ll P=1,Q=1;
		for (int j=1;j<=n;j++)
			if (i!=j){P=P*(k-x[j])%MOD; Q=Q*(x[i]-x[j])%MOD;}
		ans=(ans+y[i]*P%MOD*qpow(Q,MOD-2)%MOD)%MOD;
	} printf("%lld",(ans%MOD+MOD)%MOD);
	return 0;
}

这里因为是模 $998244353$ 意义下的，所以用了逆元 .

其截断误差由如下定理得出

若 $f(x)\in C^{n+1}[a,b]$，$L(x)$ 是 $f$ 在区间 $[a,b]$ 上 $n+1$ 个不同点 $x_0,x_1,⋯,x_n$ 上的次数不超过 $n$ 的插值多项式，则对每个 $x\in[a,b]$ 都存在 $\xi_x\in [a,b]$ 满足：

$$f(x)-L(x)=\dfrac{1}{(n+1)!}f^{(n+1)}(\xi_x)\prod_{i=0}^n(x-x_i)$$

证明见 * 一节 .

注意到利用定理估计截断误差实际上很困难，一是因为上式要计算 $f(x)$ 高阶导数，二是 $\xi_x$ 的位置不确定 .

若有 $n+2$ 组数据，前 $n+1$ 个做一次插值，后 $n+1$ 个做一次插值，然后相减化一下式子即可获得比较实用的公式 .

2. 当 $x_i$ 连续时的更优做法

不妨加上 $x_i=i$，则有

$$L_n(x)=\sum_{i=0}^ny_i\prod_{i\neq j}\dfrac{x-j}{i-j}$$

维护 $k-j$ 的前缀积，后缀积和阶乘即可 .

3. 重心拉格朗日插值

注意到每次新加入一个点的时候要重新插值，如果要多次增加点，拉格朗日插值就 gg 了 .

先看一下前面的式子

$$L_n(x)=\sum_{i=0}^ny_i\prod_{i\neq j}\dfrac{x-x_j}{x_i-x_j}$$

设

$$g=\prod_{i=0}^n(k-x_i)$$

则

$$L_n(x)=g\sum_{i=0}^n\prod_{i\neq j}\dfrac{y_i}{(x-x_i)(x_i-x_j)}$$

发现只有 $x-x_i$ 是变化的，则令

$$w_i=\dfrac{y_i}{x_i-x_j}$$

从而

$$L_n(x)=g\sum_{i=0}^n\prod_{i\neq j}\dfrac{w_i}{x-x_i}$$

每次加点时 $O(n)$ 算出 $w_i$ 即可求出新的 $L_n(x)$ .

3. 快速插值

1. $O(n\log^3 n)$ 插值

咕

2. $O(n^2\log^2 n)$ 插值

咕

3. $O(n\log^2 n)$ 插值

咕

4. 一些例题

1. 自然数 $k$ 次方和

给定 $n,k$，求 $\sum\limits_{i=1}^ni^k$ 对 $10^9+7$ 取模的结果 .

先对 $k$ 一定的序列差分，然后发现是 $k$ 次的，所以原式是 $k+1$ 次的，取 $1\sim k+2$ 跑拉格朗日插值即可 .

typedef long long ll;
const int N=2e6+5,MOD=1e9+7;
ll pre[N],suf[N],fac[N],n,k;
ll qpow(ll a,ll n)
{
	ll ans=1;
    while (n)
    {
        if (n&1) ans=ans*a%MOD;
        a=a*a%MOD; n>>=1;
    } return ans%MOD;
}
int main()
{
	scanf("%lld%lld",&n,&k); pre[0]=suf[k+3]=fac[0]=1;
	for (int i=1;i<=k+2;i++) pre[i]=pre[i-1]*(n-i)%MOD;
	for (int i=k+2;i>=1;i--) suf[i]=suf[i+1]*(n-i)%MOD;
	for (int i=1;i<=k+2;i++) fac[i]=fac[i-1]*i%MOD;
	ll tmp=0,ans=0;
	for (int i=1;i<=k+2;i++)
	{
		tmp=(tmp+qpow(i,k))%MOD;
		ll P=pre[i-1]*suf[i+1]%MOD,Q=fac[i-1]*((k-i)&1?-1:1)*fac[k+2-i]%MOD;
		ans=(ans+tmp*P%MOD*qpow(Q,MOD-2)%MOD)%MOD;
	} printf("%lld\n",(ans+MOD)%MOD);
	return 0;
}

*. 有关定理的证明

1. 多项式插值定理

若 $x_0,x_1,\cdots,x_n$ 是不同实数，则对任意实数 $y_0,y_1,\cdots,y_n$ 存在唯一的次数最多是 $n$ 次的多项式 $f(x)$ 满足 $f(x_i)=y_i$ .

Proof：

设 $f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0$，则有

$$\begin{cases}a_nx_0^n+a_{n-1}x_0^{n-1}+\cdots+a_1x_0+a_0\\a_nx_1^n+a_{n-1}x_1^{n-1}+\cdots+a_1x_1+a_0\\a_nx_2^n+a_{n-1}x_2^{n-1}+\cdots+a_1x_2+a_0\\\cdots\\a_nx_{n-1}^n+a_{n-1}x_{n-1}^{n-1}+\cdots+a_1x_{n-1}+a_0\\a_nx_n^n+a_{n-1}x_n^{n-1}+\cdots+a_1x_n+a_0\\\end{cases}$$

以 $a_0,a_1,\cdots,a_n$ 做变量，则其系数行列式

$$\begin{vmatrix}1&x_1&\cdots&x_1^n\\1&x_2&\cdots &x_2^n\\\vdots&\vdots&\ddots&\vdots\\1&x_n&\cdots&x_n^n\end{vmatrix}=\prod_{i\neq j}(x_i-x_j)$$

这一步是由于其系数行列式为转置的范德蒙德（Vandermonde）行列式。又由于 Cramer 法则，因其系数行列式不等于 $0$，从而方程有唯一解，即多项式存在且唯一 .

$$\tag*{□}$$

2. 多项式插值误差定理

若 $f(x)\in C^{n+1}[a,b]$，$L(x)$ 是 $f$ 在区间 $[a,b]$ 上 $n+1$ 个不同点 $x_0,x_1,⋯,x_n$ 上的次数不超过 $n$ 的插值多项式，则对每个 $x\in[a,b]$ 都存在 $\xi_x\in [a,b]$ 满足：

$$f(x)-L(x)=\dfrac{1}{(n+1)!}f^{(n+1)}(\xi_x)\prod_{i=0}^n(x-x_i)$$

Proof：

若 $x\in\{x_0,x_1,\cdots,x_n\}$，上式显然成立 .
否则令 $\varphi(t)=f(t)-L(t)-\lambda\omega$，其中 $\omega=\prod\limits_{i=0}^n(t-x_i)$，$\lambda=\dfrac{f(x)-L(x)}{\omega(x)}$
显然 $\varphi(t)$ 至少有 $x,x_0,x_1,\cdots,x_n$ 这 $n+2$ 个不同的根，由罗尔定理，$\varphi^{(n+1)}$ 至少有一个零点 $\xi_x$，形式化的，有

$$\varphi^{(n+1)}(\xi_x)=f^{(n+1)}(\xi_x)-\lambda(n+1)!=0$$

从而，有

$$f(x)-L(x)=\dfrac{1}{(n+1)!}f^{(n+1)}(\xi_x)\prod_{i=0}^n(x-x_i)$$

$$\tag*{□}$$