浅谈简单动态规划

记号声明
1. 线性 dp
2. 区间 dp
3. 背包
4. 数位 dp
5. 图上 dp
6. 状压 dp（状态压缩 dp）
7. 概率 dp / 期望 dp
8. dp 优化
杂项

记号声明

\(\lor\)：按位或
\(\land\)：按位与
\(\oplus\)：按位异或
\(\operatorname{shr}\)：右移
\(\operatorname{shl}\)：左移
\(\overline{A_1A_2\cdots A_n}\)：将 \(A_1,A_2,\cdots,A_n\) 顺次连接后组成的十进制数
\(\varphi\)：欧拉函数
\(P\)：概率
\(E\)：期望 / 边集（你可以把 \(\sum\limits_{(u,v)\in E}\) 看做是枚举 \(u\) 的所有出点 \(v\)）
\(\overline{A}\)：\(A\) 的否定
\(\gets\) / \(\to\)：赋值
\([B]\)：指示函数，定义为 \([B]=\begin{cases}1&B\,为真\\0&B\,为假\end{cases}\)

1. 线性 dp

入门线性 dp

Problem 1 填满网格
给出一个 \(2\times n\) 的网格，你现在需要用 \(n\) 个 \(1\times 2\)的多米诺骨牌占满整个棋盘。
多米诺骨牌可以横着或者竖着放。
求有多少方案数占满整个棋盘。

令 \(dp_n\) 为选到第 \(n\) 列的方案数，则

\[dp_n=dp_{n-1}+dp_{n-2} \]

可以 \(O(n)\) 递推，也可以矩阵快速幂优化到 \(O(\log n)\) .

Problem 2 网格图路径计数
给出一个 \(n\times m\) 的网格，每次只能向右或者向下走（其中有些位置是不能走到的），求从 \((1,1)\) 走到 \((n,m)\) 的方
案数 .

令 \(dp_{n,m}\) 为走到 \((n,m)\) 的方案数即可

Problem 3 LCIS
求最长公共上升子序列 .

设要找 LCIS 的两个字符串为 \(S,T\) .

令 \(dp_{i,j}\) 表示 \(S\) 前 \(i\) 个位置和 \(T\) 前 \(j\) 个位置所能产生的 LCIS 的长度，

若 \(S_i\neq B_j\) 则 \(dp_{i,j}=0\) .

我们从 \(1\cdots n\) 枚举 \(i\) 计算 dp 值，在枚举的过程中维护

\[S_k=\max_{1\le j<i}\{dp_{j,k}\} \]

从而

\[dp_{i,j}=\max_{k<j\,且\,B_k<A_i}\{S_k\}+1 \]

如果我们再从小到大边枚举 \(j\) 边记录满足条件的 \(S_k\) 最大值即可。

时间复杂度 \(O(nm)\) .

进阶线性 dp

Problem 4
有 \(m\) 个码头和 \(e\) 条航线，每天航线有成本。有连续 \(n\) 天需要从 \(1\) 号码头到 \(m\) 号码头运输货物。每个码头会在某些天数区间内不许经过。每更换一次运输路线，要付出 \(k\) 的成本 .
求这 \(n\) 天的最小总成本。
\(1\le m\le 20\)，\(1\le n\le 100\) .

预处理 \(dis(x,y)\) 为 \(x\) 到 \(y\) 天都能用的路径长度（跑个最短路径即可），令 \(dp_i\) 表示前 \(i\) 天的最少运输成本，则

\[dp_i=\min_{j<i}\{dp_j+w(j+1,i)\cdot(i-j)+k\} \]

时间复杂度 \(O(n^2m\log m)\) .

Problem 5
https://www.luogu.com.cn/problem/P4158

当 \(n=1\) 时，令 \(w(x,y)\) 为 \(x\) 到 \(y\) 直接的最大同色格子数（前缀和解决），令 \(dp_{i,j}\) 表示前 \(i\) 个格子刷 \(j\) 次的最多正确格子数，则

\[dp_{i,j}=\max_{k<i}\{dp_{k+1,i}+w(k+1,i)\} \]

当 \(n\ge 1\) 时，令 \(D_{i,j}\) 表示前 \(i\) 个木板刷 \(j\) 次的最多正确格子数，则

\[D_{i,j}=\max_{k\le j}\{D_{i-1,k}+dp(i)_{m,j-k}\} \]

其中 \(dp(S)_{\dots}\) 表示第 \(S\) 个木板前 \(i\) 个格子刷 \(j\) 次的最多正确格子数 .

括号序列模型

这里先引入两条括号序列的性质：

括号序列性质 1
将左括号看成 \(+1\)，右括号看成 \(-1\)，括号序列匹配的充要条件任意一个前缀和大于等于 \(0\)，且总和为 \(0\) .

括号序列性质 2
删去括号序列中匹配的括号，不影响括号序列的合法性 .

Problem 6
给定一个长度为 \(n\) 的仅包含 ( 和 ? 的字符串，将问号变成 ( 或 ) 使得该括号序列合法，求方案总数 .
\(1\le n\le 3000\) .

令 \(dp_{i,j}\) 表示当前到第 \(i\) 个字符，现在还有 \(j\) 个左括号 .

运用括号序列性质 1，分 \(3\) 种情况考虑：

若第 \(i+1\) 个字符是 (，则能转移到 \(dp_{i+1,j+1}\) .
若第 \(i+1\) 个字符是 )，则能转移到 \(dp_{i+1,j-1}\) .
若第 \(i+1\) 个字符是 ?，则两者皆能转移到 .

最终 \(dp_{n,0}\) 就是方案总数啦，时间复杂度 \(O(n^2)\)

Problem 7
在一款电脑游戏中，你需要打败 \(n\) 只怪物（从 \(1\) 到 \(n\) 编号）。为了打败第 \(i\) 只怪物，你需要消耗 \(d_i\) 点生命值，但怪物死后会掉落血药，使你恢复 \(a_i\) 点生命值，任何时候你的生命值都不能降到 \(0\) 或 \(0\) 以下 .
请问是否存在一种打怪顺序，使得你可以打完这 \(n\) 只怪物而不死掉 .
\(1\le n\le 10^5\) .

贪心：

若 \(a_i-d_i\ge 0\)，按 \(d_i\) 排序一个个杀即可 .
若 \(a_i-d_i <0\)，假设剩余血量为 \(H\)，那么 \(H\) 是固定的，可以看作初始血量为 \(H\)，怪兽的属性 \(a,d\) 交换，这样就和上一种情况一样了 .

Problem 8
给出一些括号序列，要求选择一些括号序列拼接成一个合法的括号序列，使得总长最大。

删去匹配的，跑一边 Problem 7，然后做 dp，令 \(dp_{i,j}\) 为前 \(i\) 个括号序列左括号比右括号多 \(j\) 个时的最长的长度和，设 \(len_i\) 为排完序后第 \(i\) 个括号序列的长度，考虑下一个括号序列选不选即可 .

时间复杂度 \(O(n\cdot len^2)\)

记忆化搜索

记忆化搜索本不是什么大类，故在「线性 dp」里稍提一句 .

做一些转移顺序很怪的题的时候可以记忆化搜索 .

例题：
https://www.luogu.com.cn/problem/P1434

2. 区间 dp

令 \(dp_{l,r}\) 为 \(l\) 到 \(r\) 之间的最优方案 / 方案数，每次转移枚举一个中间点 \(k\)，考虑合并区间即可 .

Problem 1
https://www.luogu.com.cn/problem/P1880

令 \(dp_{l,r}\) 表示从 \(l\) 到 \(r\) 的石子合并到一起的最大价值，枚举一个中间点 \(k\)，则：

\[dp_{i,j}=\max_{k\in[i,j)}\{dp_{i,k}+dp_{k+1,j})+\sum_{k=i}^{j}a_i \]

最后这个求和可以前缀和优化 .

注意区间 dp 题要先枚举长度 \(l\)，然后枚举起始点 \(l\)，通过它们推出 \(r\)，然后再枚举中间点 \(k\)（因为要从小区间推到大区间）.

区间 dp 有一个非常朴素的处理环形问题的方法，破环为链（也有叫断环为链、破环成链、断环成链的），就是把环在随便一个地方拆成序列，然后把序列复制一份丢到后面 .

区间 dp 题其实都差不多，可以做做 poj3280，Codeforces 245H， [NOIP2006 提高组] 能量项链，[USACO06FEB]Treats for the Cows G/S .

当然有些区间 dp 不用枚举中间点（通过处理边界进行转移） .

3. 背包

1. 0/1 背包

题目：https://www.luogu.com.cn/problem/P1048

令 \(dp_{i,j}\) 表示前 \(i\) 个物品 \(j\) 的重量时的最大价值 .

讨论最后一个物品选不选即可，

\[dp_{i,j}=\max\{dp_{i-1,j},dp_{i-1,j-w_i}+v_i\} \]

（\(w_i\) 是重量，\(v_i%%%\) 是价值）

时间复杂度 \(O(nm)\) .

记录方案数：讨论转移情况 .
记录方案：倒推或者记录 pre .

注意如果滚动数组必须倒序循环，因为要保证状态不能被提前更新 .

2. 完全背包

题目：https://www.luogu.com.cn/problem/P1616

令 \(dp_{i,j}\) 表示前 \(i\) 个物品 \(j\) 的重量时的最大价值，类似的，有：

\[dp_{i,j}=\max\{dp_{i-1,j},dp_{i,j-w_i}+v_i\} \]

这里滚动数组就得正序了 .

在这里提一下一个贪心的预处理：
对于所有 \(w_i\ge w_j\)，\(v_i\le v_j\) 的物品 \(j\)，可以直接丢掉，
对于体积相同的物品只需要留下价值最大的物品 .
对于随机数据这个优化的力度非常大 .

3. 多重背包

每个物品最多用 \(t_i\) 次 .

最暴力的方法就是转移的时候枚举这个物品选几个即可 .

时间复杂度 \(O(nm\max\{t_i\})\)

优化 \(1\)（二进制分组）：把物品二进制分组后跑 01 背包即可，时间复杂度 \(O(nm\log\max\{t_i\})\).

优化 \(2\)（单调队列优化）：我们来观察一下式子：

\[dp_{i,j}=\max_{k\le t_i}\{dp_{i-1,j-k\cdot w_i}\}+k\cdot w_i \]

注意到最后一维关于 \(w_i\) 同余，故按照同余类分类 .

令 \(S_j=dp_{i-1,j\cdot w_i+r}\)，则

\[\begin{aligned}dp_{i,j\cdot w_i+r}&=\max_{j-k\le t_i}\{S_k+(j-k)v_k\}\\&=\max_{j-k\le t_i}\{S_k-k\cdot v_k\}+j\cdot v_k\end{aligned} \]

发现这事滑动窗口，单调队列优化即可 .
时间复杂度 \(O(nm)\) .

注意如果要求方案数，把单调队列换成前缀和，做法仍然正确 .

但是如果用二进制分组就不正确了~~，读者自证不难~~ .

4. 分组背包

题目：https://www.luogu.com.cn/problem/P1757

Simple！此题很容易，留作习题答案略（？）

5. 树上背包

见「树形 dp」一节

6. 二维费用背包

加一维费用即可 .

7. 泛化物品

给你一些房间，告诉你这些房间的容纳人数和价格。
安排一定数量的人住到旅馆里，满足：

不同性别的人如果不是夫妻那么不能住一个房间 .

一对夫妻如果住在一起，那么房间不能安排其他的人进去哪怕房间没盛满人 .

你来写一个程序帮助佳佳找到安排这些来参加旅行的人住进旅馆所需要的最小花费 .

不难发现，要么至多存在 \(1\) 对夫妻住在一起，要么不存在夫妻住在一起 .

令 \(dp_{i,j,k,0/1}\) 表示前 \(i\) 个房间住 \(j\) 名男性 \(k\) 名女性并且没有夫妇（0） / 有夫妇（1）住在一起的最小花费 .

讨论入住的人即可转移 .

8. 物品重量形如 \(a\cdot 2^b\)，背包容量很大时的 01 背包

题目：https://www.luogu.com.cn/problem/P3188

按 \(2^b\) 分组：

将物品按 \(b\) 值从大到小排序分阶段处理，在阶段内 \(b\) 值都相同，直接忽略不足 \(2^b\) 的部分 .

令 \(dp_{i,j}\) 表示前 \(i\) 个物品，剩余的能用重量为 \(j\cdot 2^b\) 的最大价值

从而 \(dp_{i,j}\gets dp_{i-1,j}\qquad dp_{i,j}\gets dp_{i-1,j+a}\)

从上一阶段到下一阶段时，将 \(dp_{i,j}\to dp_{i,2j+something}\)，注意到 \(n\le 100\quad a\le 10\)

所以剩余重量最多记录到 1000 即可，时间复杂度 \(O(1000n)\) .

9. 一类整数划分问题

一些用生成函数 & 多项式求解的整数划分问题这里不再提（因为题目叫「浅谈简单动态规划」嘛），要了解请到十二重计数法 .

P.S. 我们将 \(n,k,m\) 看做同阶以评价问题时间复杂度的优秀与否 .

1. 求把 \(n\) 划分成 \(k\) 个正整数的方案数

本质是个完全背包的，可以做到 \(O(n^2k)\)，暴力 dp 的复杂度是 \(O(n^2k\log n)\) 的 .

更优方案：令 \(dp_{i,j}\) 为把 \(i\) 划分成 \(j\) 个正整数的方案数，则

考虑有没有 \(1\)，可以得到

\[dp_{i,j}=dp_{i-j,j}+dp_{i-1,j-1} \]

复杂度易得

2. 求把 \(n\) 划分成互不相同的 \(k\) 个正整数的方案数

暴力 dp 类似，这个本质是个 01 背包，也可以 \(O(n^2k)\) 解决 .

更优方案也是类似，

\[dp_{i,j}=dp_{i-j,j}+dp_{i-j,j-1} \]

这个写记搜复杂度会更低

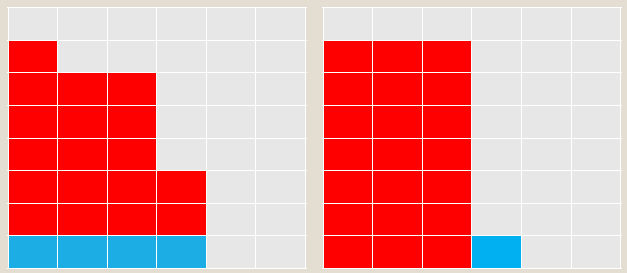
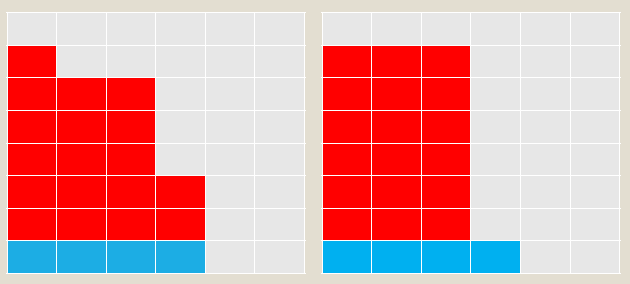
3. 求把 \(n\) 划分成 \(k\) 个不大于 \(m\) 的互不相同正整数的方案数

背包做法类似

更优方案也类似，

\[dp_{i,j}=dp_{i-j,j}+dp_{i-j,j-1}-dp_{i-m-1,j-1} \]

这里减 \(dp_{i-m-1,j-1}\) 是为了满足不大于 \(m\) 的条件，如图：

4. 数字纯奇纯偶划分

以可重复为例，不可重复同理：
令 \(dp1_{i,j}\) 为把 \(i\) 划分为 \(j\) 个偶数的方案数，\(dp2_{i,j}\) 为把 \(i\) 划分为 \(j\) 个奇数的方案数，则

\[dp1_{i,j}=dp2_{i-j,j} \]

\[dp2_{i,j}=dp2_{i-1,j-1}+dp1_{i-j,j} \]

5. 一道例题

在 \([-n,n]\) 中选 \(k\) 个不同整数，问和为 \(0\) 的方案数 .

显然求出来 \(dp_{i,j}\) 表示选出 \(j\) 个数和为 \(i\) 的方案数（把 \(n\) 划分成互不相同 \(k\) 个正整数的方案数），然后枚举其中一端拿走几个 \(a\) ，以及拿走的数的重量之和 \(x\)，把 \(dp_{x,a}\cdot dp_{x,k-a}\) 累加之和就是最后的答案 .

时间复杂度 \(O(nk^2)\) .

6. ？

dp 问题中，转移就是分情况讨论，每种情况对应一个方案数或最优值，而这个方案数或最优值可以表示为之前已经求出来的 dp 值的组合 .

只不过分情况讨论可能方法很多，以一种方式讨论能转化为已知的 dp 值的叠加，另一种方式也可以。我们需要保证的是：讨论不漏掉任何情况，像计数问题也不能出现方案重叠（求 \(\max\)、\(\min\)、\(\gcd\)、\(\operatorname{lcm}\) 这种其实是可以重叠的），同时选择分类项数尽量少的方案，以便得到更优的复杂度 .

上面几道题的转移方式可能没有原先一些问题的分类方式直观，但是也的确满足了不重不漏尽量简洁的条件。当然这可能也并非是唯一的转移方式，只要保证能划归到之前已经求出的 dp 值就行 .

分类讨论要不重不漏（求方案数问题）（正确性）
讨论时要保证划归到的 dp 状态已经求出来，而不是还未求的（正确性）
尽量分的类少一些，转移更快速。（复杂度）

4. 数位 dp

就事一位一位的 dp，在一道例题中说明罢：

1. Windy 数

题目：https://www.luogu.com.cn/problem/P2657

代码：

int dp[N][2][2][N],a[N]; // a 是数字
int dfs(int loc,bool limit,bool lead,int pre)
// loc : 位置
// limit : 是否有上界限制（这对 maxbit 有影响）
// lead : 是否有前导零（这对条件判断有影响）
// pre : 前一个数（这对条件判断有影响）
{
	if (!loc) return 1; // 从大到小，如果到终点了，直接 return
	if (dp[loc][limit][lead][pre]!=-1) return dp[loc][limit][lead][pre]; // 如果算过，就返回（记忆化搜索）
	int ans=0,maxbit=limit?a[loc]:9; // 最高位判断
// 何为最高位判断？
// dp 时，要算 1~n 内的数字有几个满足的，这样套个减法就是 [l,r] 之间的数字有几个，套个二分就是第 k 个是什么 .
// 举个例子，当数字是 234 时：
// 110,111,112,...,119 均可以 dp 到
// 231,232,233,234 只能 dp 到 234
// 此处的 maxbit 就是这个作用
	for (int i=0;i<=maxbit;i++)
		if (lead||abs(pre-i)>=2) ans+=dfs(loc-1,limit&(i==a[loc]),lead&(i==0),i); // 如果满足条件，那么转移
	return dp[loc][limit][lead][pre]=ans; // 返回
}
int solve(int q)
{
	memset(dp,-1,sizeof dp); // 一定要用 -1，不要用 0
	int len=0;
	while (q){a[++len]=q%10;q/=10;} // 分解数字
	return dfs(len,1,1,0);
}

2. 花神的数论题

题目：https://www.luogu.com.cn/problem/P4317

注意到 \(\operatorname{sum}(i)\) 的最大值是 \(\log\) 级别的，所以统计每个 \(\operatorname{sum}(i)\) 出现的次数，然后上个快速幂即可 .

统计次数的时候不要随意取模，因为取模要对 \(\varphi(10^7+7)=9984400\) 取模，容易误以为 \(10^7+7\) 是质数而错误求解答案 .

当然我用的是数位 dp 时用乘法统计答案：

ll dp[N][N],n;
bool a[N];
ll dfs(int loc,int sum,bool limit)
{
	if (!loc) return max(sum,1);
	if ((dp[loc][sum]!=-1)&&!limit) return dp[loc][sum];
	ll ans=1,maxbit=limit?a[loc]:1;
	for (int i=0;i<=maxbit;i++)
		ans=(ans*dfs(loc-1,sum+i,limit&(i==maxbit)))%MOD;
	if (!limit) return dp[loc][sum]=ans;
	else return ans;
}

ll solve(ll n)
{
	memset(dp,-1,sizeof dp);
	int len=0;
	while (n){a[++len]=n&1; n>>=1;}
	return dfs(len,0,1);
}
// 答案是 solve(n) .

3. 数字计数

题目：https://www.luogu.com.cn/problem/P4999

设 \(dp_{q,i}\)（\(i\in\{0,1,2,3,4,5,6,7,8,9\}\)）为 \(1\sim q\) 中 \(i\) 出现的次数，\(1\sim q\) 的数字和显然就是 \(dp_{q,0}\times 0+dp_{q,1}\times 1+\cdots+dp_{q,i}\times i\cdots+dp_{q,9}\times 9\)。

所以我们只需要求出 \(1\sim q\) 中 \(i\) 出现的次数就能解决这个问题了。

这个问题看起来很好解决，但是注意前导零会影响结果，所以不能有前导零。

这该怎么办呢？

有前导零的式子很容易推出。有 \(q\) 位数字，\(i\) 数码的出现次数对于 \(x\in\{s\mid s\in \mathbb N,10^q\le s\le10^{q+1}\}\) ，\(f(q,i)\) 的数量都是相等的（设 \(f(q,i)\) 为 \(q\) 位数 \(i\) 数码的出现次数）。

具体求法罢，是：
\(\begin{cases}f(q,i)=0&q=0\\f(q,i)=10f(q-1)+10^{q-1}&q>0\end{cases}\)

我们考虑减去多余的 \(0\)。

我们先设数字为 \(\overline{A_1A_2A_3\dots A_n}\)

我们首先考虑求 \(\overline{A_100\dots 0}\)，将 \(\overline{A_100\dots 0}\) 分割为区间 \([0000,1000),[1000,2000),\dots,[\overline{(A_1-1)00\dots 0},\overline{A_100\dots 0})\)，所以答案就为 \(10^{n-1}A_1\)，注意 \(<A_1\) 的每个数还出现了 \(10^{n-1}\) 次，所以要加上。

首位 \(A_1\) 出现了 \(\overline{A_2A_3\dots A_n}+1\) 次，答案还要加上 \(\overline{A_2A_3\dots A_n}+1\)，

当然还需要处理前导 \(0\)，用排列组合算一下会知道 \(i\) 位 \(q\) 个前导零的数量就是 \(10^q\)（\(q\in\{s\mid s\in\mathbb N,0\le s\le i-1\}\)），把它们加起来会发现一共出现了 \(10^{i-1}+10^{i-2}+...10\)（\(\sum\limits_{k=0}^{i-1}10^k\)）次，减一下即可。

Code:

#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=51,MOD=1e9+7; //注意能 MOD 的地方都要 MOD，不然会 WA 0pts。
ll pow10[N],dp[N],a[N],count[N],tmpcount[N],ans;
// pow10    : 字面意思，10^n
// dp       : 不考虑前导零的状况
// count    : 统计 0~9 出现次数
// tmpcount : 暂时保存 count，用来减
// ans      : 累加答案
void init() //预处理 pow10 和 dp。
{
	pow10[0]=1;
	for (int i=1;i<30;i++) dp[i]=(dp[i-1]*10%MOD+pow10[i-1])%MOD,pow10[i]=10*pow10[i-1]%MOD;
}
void solve(ll x)
{
	int len=0;
	while (x){a[++len]=x%10;x/=10;} //数位分离
	for (int i=len;i>=1;i--)        //从高到低遍历
	{
		for (int j=0;j<10;j++) count[j]+=dp[i-1]*a[i],count[j]%=MOD;  //分割区间
		for (int j=0;j<a[i];j++) count[j]+=pow10[i-1],count[j]%=MOD; //加上 10^(n-1)
		ll lastnum=0;
		for (int j=i-1;j>=1;j--) lastnum=lastnum*10+a[j],lastnum%=MOD; //求出 A2A3A4...An
		count[a[i]]+=lastnum+1,count[a[i]]%=MOD;
		count[0]-=pow10[i-1],count[0]=(count[0]+MOD)%MOD; //减去前导零
	}
}
int main()
{
	init();
	ll l,r,T;
	cin>>T;
	for (int q=0;q<T;q++)
	{
		ans=0; cin>>l>>r;
		solve(r); //前缀和思想相减 r 和 l-1。
		for (int i=0;i<10;i++) (tmpcount[i]=count[i]),count[i]=0; //复制 count，记得清零
		solve(l-1);
		for (int i=0;i<10;i++) ans=(ans+i*(tmpcount[i]-count[i]+MOD)%MOD)%MOD,count[i]=0; //累加答案，记得清零 count。
		cout<<ans<<'\n';
	}
	return 0;
}

5. 图上 dp

1. 拓扑图上 dp

就是沿着拓扑序 dp，可以在拓扑的时候顺便 dp 了 .

例题：
https://www.luogu.com.cn/problem/P3183

转移：

\[dp_u=\sum_{(v,u)\in E}\{dp_v\} \]

2. 树上 dp（树形 dp）

1. 基础树形 dp

1. 树上最大独立集

给定一棵 \(n\) 个点的树，求一个最大的点集使得其中的点两两没有边相连（没有上司的舞会）.

\(dp_{u,0/1}\) 表示做完了 \(i\) 的子树， \(i\) 点是否选的最大独立集，从而：

\[dp_{u,0}=\sum_{(u,v)\in E}\max\{dp_{v,0},dp_{v,1}\} \]

\[dp_{u,1}=\sum_{(u,v)\in E}dp_{v,0}+1 \]

Code:

void dfs(int u,int fa)
{
	dp[u][1]=1; dp[u][0]=0;
	int S=g[u].size();
	for (int i=0;i<S;i++)
	{
		int v=g[u][i];
		if (v==fa) continue;
		dfs(v,u);
		dp[u][1]+=dp[u][0];
		dp[u][0]+=max(dp[u][0],dp[u][1]); 
	}
}

2. 树的直径

给定一棵 \(n\) 个点的树，求树上最远的两个点之间的距离 .
设 \(dp_i\) 表示 \(i\) 这个点到子树里面的最远点是多远的，然后把最大值和次大值加起来即可 .

1,2 的类似问题

求树的重心
求树的最大覆盖集
求树的最大权独立集

3. Tree chain problem

题目：http://acm.hdu.edu.cn/showproblem.php?pid=5293

令 \(dp_x\) 为以 \(x\) 为根的子树内选取不相交树链的价值和的最大值，枚举一条 LCA 为 \(x\) 的链 \((u,v,w)\)，那么当前方案的价值为 \(w\)加上去除 \(u\) 到 \(v\) 路径上
的点后深度最小的点的 \(dp\) 值的和。

时间复杂度 \(O(nm)\)
树链剖分优化可以做到 \(O(m\log^2n)\)

4. 三色二叉树

题目：https://www.luogu.com.cn/problem/P2585

\(dp_{i,0/1/2}\) 分别表示根是绿红蓝三种颜色时的最多/最少绿色数量即可 .

5. 小奇挖矿

题目：https://darkbzoj.tk/problem/4711

考虑 \(dp_{i,j}\) 表示 \(i\) 的子树内所有点都确定了往哪送，并且 \(i\) 送到 \(j\) 号点，并且准确来说是 \(j\) 号点 \(k\) 的代价还没计入 dp 值内的最小代价，

考虑转移，首先 \(dp_{i,j}\) 要加上从 \(i\) 到 \(j\) 的代价，然后考虑 \(i\) 的每一个儿子 \(son\)，如果 \(son\) 也运到 \(j\) ，那么这个子树的代价就是 \(dp_{son,j}\) .

如果 \(son\) 运到一个不等于 \(j\) 的点 \(F\)，那么 \(F\) 一定在以 \(i\) 为根的子树里，这样每个被建立的仓库只会被算一次 .

其实就是在 \(j\) 号点控制的联通块的根出记上 \(k\) 的花费以保证这个点 \(k\) 的花费被记到 dp 值恰好一次 .

最终答案为 \(\min\{dp_{1,i}\}+k\)

时间复杂度 \(O(n^3)\)

2. 树上背包（一般指树上 01 背包）

给出一棵 \(n\) 个点的有根树，每个节点都是一个物品，具有价值 \(V_i\) 和重量 \(W_i\) ，如果一个物品要被选择，那么它的父亲必须被选择 .
求选择的物品重量和不超过 \(m\) 的最大价值和 .
\(n,m\le 1000\) .

1. 简化版

\(W_i=1\) .

\(dp_{i,j}\) 表示在以 \(i\) 为根子树中选择，\(i\) 强制选择，选择 \(j\) 个点的最大价值，转移时每次将一个孩子暴力合并到父亲上，合并就枚举这个孩子内部选择了多少点即可：

\[dp_{i,j}=\max_{k\in[0,j)}\{dp_{i,j-k}+dp_{son,k}\} \]

这事均摊 \(O(n^2)\) 的.

2. 普通版 - 暴力

再用前面的做法就是 \(O(n^3)\) 的了，会 T

注意到我们这里两个一维数组的背包合并是 \(n^2\) 的，所以慢，
但一个一维数组和一个单独的物品合并是线性的。.

3. 普通版 - dfs 序上 dp

在 dfs 序上 dp，如果不选一个点，则跳过代表他的子树的 dfs 上连续一段，预处理跳过的距离然后跑 01 背包即可 .

4. 普通版 - 奇怪做法

直接把 dp 数组复制再传给孩子，再从孩子递归下去，最后原来自己的 dp 数组和孩子的 dp 数组直接在对应重量的价值中取 \(\max\) .

3. 换根 dp

有些问题我们只需要处理子树的信息就可以计算出全部答案，但是还有一些问题需要知道祖先的信息，这一类问题我们会做两遍 dfs：

第一遍求出每个点子树内的信息；
另一遍从根往下遍历的时候计算维护出每个点祖先的信息。

这个相当于把儿子当成根了 .

注意到第二遍 dfs 过程中就求出了每个点祖先的信息，这样该点所需计算答案的所需信息都有了，对应的算答案就好。

Problem 1

一棵边带权值 \(n\) 个点的树，求每个点在树上的最远距离 .

方法 1：显然每个点的最远点一定在直径的两端其中一个，两遍 dfs 求出直径然后再求最短路即可 .

方法 2（换根 dp 做法）：

在代码里说明：

void dfs_up(int u)
{
	int S=g[u].size();
	for (int i=0;i<S;i++)
	{
		int v=g[u][i].first,w=g[u][i].second;
		dp[v][2]=max(dp[u][2],dp[v][0]+w==dp[u][0]?dp[u][1]:dp[u][0])+w;
		dfs_up(v);
	}
}

\(dp_{u,0}\) 是向下最长；
\(dp_{u,1}\) 是向下次长；
\(dp_{u,2}\) 是向上最长；

它们三个取 \(\max\) 就是点 \(u\) 的答案 .

3. 基环树上 dp

一般方法

断开环上一条边，枚举边端点的情况，然后当树来处理 .
先把环上挂着的树的信息都计算完，然后转化为环形的序列问题 .

注意一定要

找环

无向：dfs 找返祖边

特殊有向：转成内向树在暴力循环

6. 状压 dp（状态压缩 dp）

状压 dp 一般数据范围非常小，思想就是在 dp 维度里面加个状态 .

看个例子：

1. 「棋盘」类

常用位运算技巧

取出 \(x\) 的第 \(i\) 位：(x>>(i-1))&1 .
将 \(x\) 的第 \(i\) 位置零：x|(1<<(i-1)) .
将 \(x\) 的第 \(i\) 位置一：x&(~(1<<(i-1))) .
将 \(x\) 的第 \(i\) 位取反：x^(1<<(i-1)) .
将 \(x\) 最靠右的 \(1\) 变成 \(0\)：x&(x-1) .
取出 \(x\) 最靠右的 \(1\)（lowbit）：x&(-x) .
把最靠右的 \(0\) 变成 \(1\)：x|(x+1) .
判断是否有两个连续的 \(1\)：if (x&(x<<1))
判断是否有 \(n\) 个连续的 \(1\)：if ((x&(x<<1))&&(x&(x<<2))&& ... &&(x&(x<<n)))
枚举子集：

for (int s=1;s<(1<<n);s++) // start statu
	for (int now=s;now;now=(now-1)&s)
		// do something

值得一提的是这个枚举子集是 \(O(3^n)\) 的 .

1. 经典题

给出一个 \(n\times m\) 的棋盘，要放上一些棋子，要求不能有任意两个棋子相邻 .
求方案数 .
\(n\le 100\quad m\le 8\) .

令 \(dp_{i,S}\) 表示到第 \(i\) 行，第 \(i\) 行的状态是 \(S\) 的方案数（\(S\) 是一个二进制数，如果 \(S\) 的第 \(j\) 位为 \(1\)，则表明第 \(i\) 行第 \(j\) 列有一枚棋子）

转移只是枚举罢了：

\[dp_{i,S}=\sum_{S\land S'=0}dp_{i-1,S'} \]

这里 \(S\land S'=0\) 表明上下没有相邻棋子 .

时间复杂度 \(O(n2^m)\)，注意到 \(m\) 很小，故可以通过此题 .

2. 互不侵犯

题目：https://loj.ac/p/2153

\(dp_{i,k,S}\) 表示放完前 \(i\) 行，放了 \(k\) 个国王，第 \(i\) 行状态为 \(S\) 的方案数 .

转移类似

3. 蒙德里安的梦想

题目：https://www.acwing.com/problem/content/293/
数据范围改成 \(n\le 100,m\le 8\) .

这个和前两个类似，但是可以用预处理所有合法的转移方案的技巧，这样转移就是 \(O(1)\) 的了 .

2. 非「棋盘」类（？）

1. 拓扑序个数问题

给你一张拓扑图，求这张拓扑图有多少种不同的拓扑序 .

\(dp_{S}\) 表示当前选点的状态是 \(S\) 的方案数 .
转移考虑枚举下一个点选什么下一个选的点要满足它在 \(s\) 中的点选完后的入度为 0 ，也就是指向它的点都已经加进拓扑序里了，转移到 \(dp_{S\lor(1\operatorname{shl}(i-1))}\) 即可 .

2. 愤怒的小鸟

题目：https://www.luogu.com.cn/problem/P2831

两头猪加上原点即可确定抛物线，于是不同的抛物线只有 \(O(n^2)\) 种 .

令 \(dp_S\) 为已经消灭的猪的集合为 \(S\) 时的最少次数，暴力的转移方法为依次枚举抛物线去更新所有 \(dp\) 值，这样做时间复杂度为 \(O(n^22^n)\) .

更快的转移方法为从小到大枚举 \(S\)，每次打掉编号最小的还没消灭的猪由于包含该猪的抛物线只有 \(O(n)\) 种，所以时间复杂度为 \(O(n2^n)\) .

3. 交换茸角

题目：https://darkbzoj.tk/problem/3900

首先其实最终肯定是把这些鹿分成一些组，每一组内通过组的大小减一次操作来满足题目要求的条件，注意对于一个组，我们将所有的角排序，第 \(2i-1\) 和 \(2i\) 个要保证之差小于等于 \(C\)，才是合法的一组 .

其实就是选尽量多合法的组并起来等于全集，枚举子集的状态压缩 dp 即可 .

4. Travelling

题目：http://acm.hdu.edu.cn/showproblem.php?pid=3001

用三进制即可解决（没有位运算会比较慢，有个替代方案是用两位二进制拼成一个三进制）

5. LIS 2

给出一个 \(1\sim n\) 排列的其中一种最长上升子序列，求原序列可能的种数，
\(n\le 15\) .

令 \(dp_{S_1,S_2}\) 表示所选的数字集合为 \(S_1\) ，此时的做最长上升子序列题时那个辅助数组 \(h\) 状态为 \(S_2\) ，肯定只有 \(S_1\) 中的一些数出现在了 \(h\) 数组中，而 \(S_2\) 就是出现在 \(h\) 数组中的数的集合。而我们每在这个序列末尾加一个数 \(x\) ，就会在 \(h\) 中把大于 \(x\) 最小的数替换掉。而 \(S_2\) 状态中，就是把比 \(x\) 高位最近的 \(1\) 去掉，然后把 \(x\) 这位赋为 \(1\) 即可 .

转移的话枚举下一个数是什么即可，时间复杂度 \(O(n3^n)\) .

关于时间复杂度估算

\(n\le 20\) 一般是 \(O(2^n)\) 或者 \(O(n2^n)\)
\(n\le 16\) 大概率是 \(O(3^n)\)
\(n\le 15\) 大概率是 \(O(3^n)\) 或者 \(O(n3^n)\) .

7. 概率 dp / 期望 dp

1. 前置

概率就是事件可能性大小，期望就是事件平均发生结果

1. 概率

\[P(A 或 B)=P(A)+P(B)-P(A且B) \]

\[P(A)+P(\overline{A})=1 \]

\[若 A,B 互斥，则 P(A)P(B)=P(A且B) \]

2. 期望

\[E(x+c)=E(x)+c\qquad\qquad cE(x)=E(cx)\tag{c 是常数} \]

\[E(x+y)=E(x)+E(y) \]

\[若 x,y 互斥，则 E(x)E(y)=E(xy) \]

2. 一些通用技巧

若事件所产生的所有方案都是等概率的，那么一些概率与期望即可转化为一个计数问题，算出后再除以总方案数即可 .

如求事件符合条件 \(A\) 的概率，则转化为对符合 \(A\) 的方案数的计数问题；若求方案的某种价值的期望值，则转化为所有方案的价值总和的计数问题 .

概率与期望可以通过列方程的方法计算，For the example：

有 \(4\) 张卡片，写着 \(0,1,2,3\) ，每次抽出一张并放回，反复抽，抽出 \(0\) 为止。问抽取的次数的期望值 .

设抽取次数为 \(x\)，讨论取没取到，则

\[x=1+\dfrac34\cdot x+\dfrac 14\cdot 0 \]

从而 \(x=4\) .

3. 概率 dp

1. 钉子和小球

题目：https://www.luogu.com.cn/problem/P5750

令 \(dp_{i,j}\) 为小球经过第 \(i\) 行第 \(j\) 列的概率。

为了方便表示，令 \(\mathcal{P}(x,y),\mathcal{Q}(x,y)\) 表示 \((x,y)\) 有没有钉子，若有，则 \(\mathcal{P}(x,y)=1, \mathcal{Q}(x,y)=0\)，若没有，则 \(\mathcal{P}(x,y)=0, \mathcal{Q}(x,y)=1\) .

显然 \(dp_{1,1}=1\)，转移为

\[dp_{i,j}=\dfrac12\mathcal{P}_{i-1,j-1}dp_{i-1,j-1}+\dfrac12\mathcal{P}_{i-1,j}dp_{i-1,j}+\mathcal{Q}_{i-2,j-1}dp_{i-2,j-1} \]

2. 摘苹果

在花园中有 \(n\) 棵苹果树以及 \(m\) 条双向道路，每条道路的两端连接着两棵不同的苹果树 . 假设第 \(i\) 棵苹果树连接着 \(d_i\) 条道路。小 Q 将会按照以下方式去采摘苹果：

随机移动到一棵苹果树下，移动到第 \(i\) 棵苹果树下的概率为 \(\dfrac{d_i}{2m}\)，但不在此采摘 .

重复以下操作 \(k\) 次：等概率随机选择一条与当前苹果树相连的一条道路，移动到另一棵苹果树下，假设当前位于第 \(i\) 棵苹果树下，则他会采摘 \(a_i\) 个苹果，多次经过同一棵苹果树下会重复采摘。

请计算小 Q 期望摘到多少苹果。
\(n,k\le 100000\)，\(m\le 200000\)

首先容易得到一个简单的做法，令 \(dp_{i,j}\) 为走 \(i\) 步之后到达 \(j\) 的概率，那么：

\[dp_{i,j}=\sum_{(u,j)\in E}\dfrac{dp_{i-1,u}}{d_u} \]

通过对上式的简单推导（从 \(dp_{0,j}\) 出发）可以得到：

\[dp_{i,j}=\dfrac{d_j}{2m} \]

从而答案为

\[\begin{aligned}ans&=\sum_{i=1}^n\sum_{j=1}^ka_idp_{j,i}\\&=k\sum_{i=1}^n\dfrac{d_ia_i}{2m}\end{aligned} \]

4. 期望 dp

1. 抵制克苏恩

题目：https://darkbzoj.tk/problem/4832

设 \(dp_{i,a,b,c}\) 表示还要（期望 dp 一般都是倒着设状态）进行 \(i\) 轮攻击，三种血量的奴隶主数量分别为 \(a,b,c\) 时，接下来英雄受到的期望总伤害（\(dp_{0,a,b,c}=0\)） .

转移只要枚举当前攻击到的是英雄还是哪种奴隶主即可。

每次询问可以 \(O(1)\) 回答。

2. 换教室

题目：https://loj.ac/p/2360

先 Floyd 求出任意两点间最短路径，然后令 \(dp_{i,j,0/1}\) 表示前 \(i\) 个课程申请了 \(j\) 次，且第 \(i\) 个课程是否申请时的最小期望值 .

转移考虑换不换教室即可，时间复杂度 \(O(v^3+nm)\) .

3. 奖励关

题目：https://www.luogu.com.cn/problem/P2473

发现吃和不吃比较难维护，考虑上状压，令 \(dp_{i,S}\) 为还要进行 \(i\) 轮游戏，吃过的宝物集合为 \(S\) 时，接下来能得到的最大期望得分，从而

\[dp_{i,S}=\sum_{k}\dfrac 1m\max\{dp_{i-1,S},dp_{i-1,S∪\{k\}}+a_k\} \]

4. OSU!

题目：https://www.luogu.com.cn/problem/P1654

先提一句，一般情况下 \(E^3(x)\neq E(x^3)\) .

我们考虑每一个位置 \(i\) 对答案的增量的期望。

首先如果 \(i\) 之前的极长 \(1\) 串长度为 \(x\) ，下一个位置再是 \(1\) ，则这个增量就是 \(3x^2+3x+1\)（直接减）

而增量的期望就是 \(p_i(3E(x^2)+3E(x)+1)\)

再维护一下 \(E(x^2)\) 和 \(E(x)\) 即可，挺容易维护的 .

Code:

const int N=100050;
int n;
double E1[N],E2[N],ans;
int main()
{
	scanf("%d",&n); double tmp;
	for (int i=1;i<=n;i++)
	{
		scanf("%lf",&tmp);
		E1[i]=(E1[i-1]+1)*tmp;
		E2[i]=(E2[i-1]+2*E1[i-1]+1)*tmp;
		ans+=(3*E2[i-1]+3*E1[i-1]+1)*tmp;
	} printf("%.1f",ans);
	return 0;
}

8. dp 优化

关于 tD/eD 动态规划

tD/eD 动态规划指：状态空间是 \(O(n^t)\) 的，每一项依赖其他 \((n^e)\) 项 .

一般用到的只有 1D/1D 和 2D/1D .

前缀和优化

求长度为 \(n\) ，逆序对为 \(k\) 的排列有多少个，答案对 \(10^9+7\) 取模 .

排列题的一个套路，我们从小到大依次把数字插入到排列中 .

令 \(dp_{i,j}\) 表示插入了前 \(i\) 个数，产生的逆序对为 \(j\) 的排列的方案数 .

考虑 \(i+1\) 插在哪，得：

\[dp_{i,j}=\sum_{k=0}(i-1)dp_{i-1,j-k} \]

发现 \(i-1\) 事常数，所以可以前缀和优化 .

这是 \(O(nk)\) 的了，再优化可以做个容斥原理，通过之前讲的整数划分的模型 dp 求出容斥系数，即 loj6077 .

单调队列优化

Problem 1
https://www.luogu.com.cn/problem/P2569

令 \(dp_{i,j}\) 表示到第 \(i\) 天手里持有 \(j\) 的股票的最大收益，那么第 \(i\) 天有三种可能：

不买不卖：\(dp_{i-1,j}\)
买入：\(dp_{i-w-1,k}-(j-k)AP_i\)（\(k\ge j-AS_i\)）
卖出：\(dp_{i-w-1,k}+(k-j)BP_i\)（\(k\le j+BS_i\)）

对于买入，把 \((j-k)\) 拆开，然后把常量移出去，再单调队列即可 .

卖出同理 .

树状数组优化 / 线段树优化 / 矩阵快速幂优化

这个和前两个类似，都是观察转移，读者很容易使用此优化 .

斜率优化

https://www.cnblogs.com/CDOI-24374/p/14070590.html

精简状态

1. LIS

转移：

\[dp_i=\max_{a_j<a_i 且j<i}\{dp_j\}+1 \]

我们考虑找最大的 \(k\) ，满足存在 \(dp_j=k\) 且 \(a_j<a_i\) .

我们设 \(h_k\) 表示 \(dp_j=k\) 的所有 \(j\) 当中的最小的 \(a_j\)，就是说长度为 \(k\) 的 IS，最后一个元素的最小值是多少 .

不难发现 \(h_k\) 单调不降，从而我们对于一个 \(a_i\) 就可以找到最大的 \(k\) ，满足 \(h_k<a_i\)，然后 \(dp_i=k+1\)，找的过程是可以二分加速的 .

然后同时在维护出 \(h\) 序列即可。

2. 传纸条

题目：https://www.luogu.com.cn/problem/P1006

令 \(dp_{i,j,x,y}\) 为是第一张纸条到达 \((i,j)\)，第二张到达 \((k,l)\) 时最大权值（走的步数一样），注意到 \(i+j=k+l\) 压掉一维，时间复杂度 \(O(n^3)\) .

Problem 2
有 \(n\) 个数，选择其中若干数，使得每连续 \(k\) 个数中都至少有一个数被选中，且选出的数的和最小 .

令 \(dp_i\) 表示前 \(i\) 个数满足题目要求且第 \(i\) 个数被选中时选出的最小值，枚举前一个位置：

\[dp_i=\min_{i-j\le k}\{dp_j+a_i\}=\min_{i-j\le k}\{dp_j\}+a_i \]

单调队列优化这个 \(\min\limits_{i-j\le k}\{dp_j\}\) 即可 .

时间复杂度 \(O(n)\) .

Problem 3
http://acm.hdu.edu.cn/showproblem.php?pid=4374

用 \(dp_{i,j}\) 表示从 \(i\) 层走完了到达 \(i\) 层 \(j\) 位置时的最大金币数。

\(sum_{i,j}\) 表示第 \(i\) 层前 \(j\) 个房间的金币和。

转移也是同理，拆开然后常量移出去 .

杂项

1. 后效性的消除

题目：codeforces.com/gym/101502/problem/D

注意到如果第一次把 \(6\) 翻到了上面，那下一次决策的时候就不能把 \(1\) 或 \(6\) 翻上去了 .

所以令 \(dp_x\) 表示「得到 \(x\) 分的最小步数」是有后效性的 .

我们如果想消除后效性，一个常用的办法是把产生后效性的东西写进数组下标 .

令 \(dp_{x,p}\) 表示「最后 \(p\) 向上，得到 \(x\) 分的最小步数」即可消除后效性，转移就考虑 \(p\) 能转到哪些面即可 .

2. 滚动数组技巧

在很多算法中，有些空间只会被利用一次；这些空间用完了之后不释放，占着内存；我们重复利用一块比较小的内存可以解决这个问题 .

最一般的，当 \(dp_{i,something}\) 只有关于 \(dp_{i-k,something}\)（其中 \(k\le \bf CONSTANT\)，\(\bf CONSTANT\) 是常数）时即可使用滚动数组 .

这种用法不常用~~（应该说是根本用不到罢）~~，最特殊的情况是 \(k=1\) 时的情况，即

当 \(dp_{i,somethihg}\) 只有关于 \(dp_{i-1,something}\) 时的情况 .

要是完全把第一维压掉，转移顺序可能会比较麻烦（参考 01 背包），所以可以考虑让第一维变成 \(0/1\) .

一般的，起两个数组 src 和 dest：

利用 src 的信息，推出 dest 的信息
把 dest 的信息复制到 src 里面去，重复上述过程（此步利用指针复制可以 \(O(1)\) 解决）

这个通用技巧是无需考虑求值顺序的 .

3. 两道套路题

queue2

题目：https://acm.taifua.com/bzoj/p/4321.html

令 \(dp1_{i,j}\) 表示 \(1\sim i\) 的排列，有 \(j\) 组相邻的相差 \(1\)，且 \(i\) 和 \(i−1\) 不相邻的方案数；
\(dp2_{i,j}\) 表示 \(1\sim i\) 的排列，有 \(j\) 组相邻的相差 \(1\)，且 \(i\) 和 \(i−1\) 相邻的方案数；

那么考虑插入 \(i+1\) 的位置，有：

不破坏空位且不与 \(i\) 相邻
不破坏空位且与 \(i\) 相邻
破坏空位且不与 \(i\) 相邻
破坏空位且与 \(i\) 相邻

分别推一下即可，时间复杂度 \(O(n^2)\) .

LAS

题目：https://www.luogu.com.cn/problem/P3584

先破环为链，令 \(dp_{i,S}\) 表示第 \(i\) 份食物被两个人吃的状态为 \(S\) 是否有可能，这里的 \(S\) 表示的是：

0：两个人都没有吃
1：左边的人吃了右边的没吃
2：左边的没吃右边的吃了
3：左右两边都吃了

只要满足：

一个人只能吃一边。
要使得中间这个人，变了吃的方向，不会吃的更多。

posted @ 2021-02-09 20:23 Jijidawang 阅读(179) 评论(1) 编辑收藏举报

刷新页面返回顶部