树状数组学习笔记
未完待续 ...
1. 树状数组原理
1. 引入
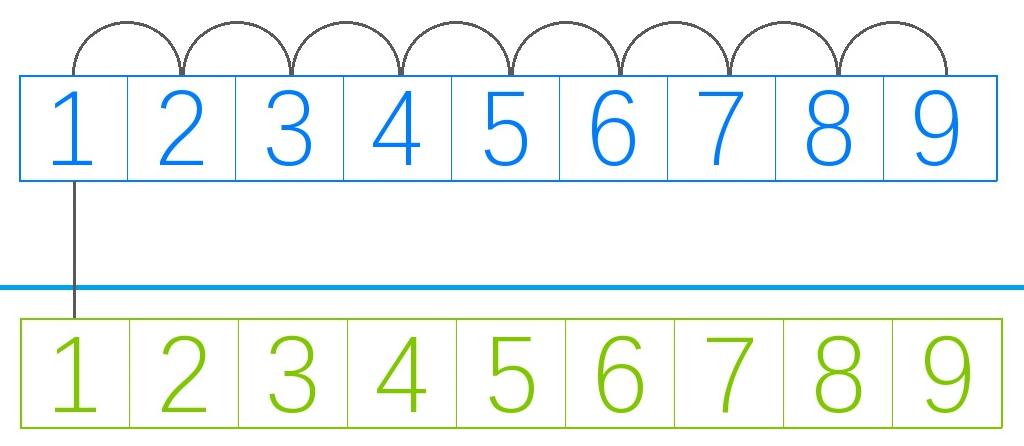
我们知道前缀和:
其中下面的为原数组 ,上面的为前缀和
我们知道,前缀和可以维护静态区间和,显然 .
但是如果要维护单点修改,区间求和的话,每次修改就要把它后面的每个前缀和修改,复杂度 .
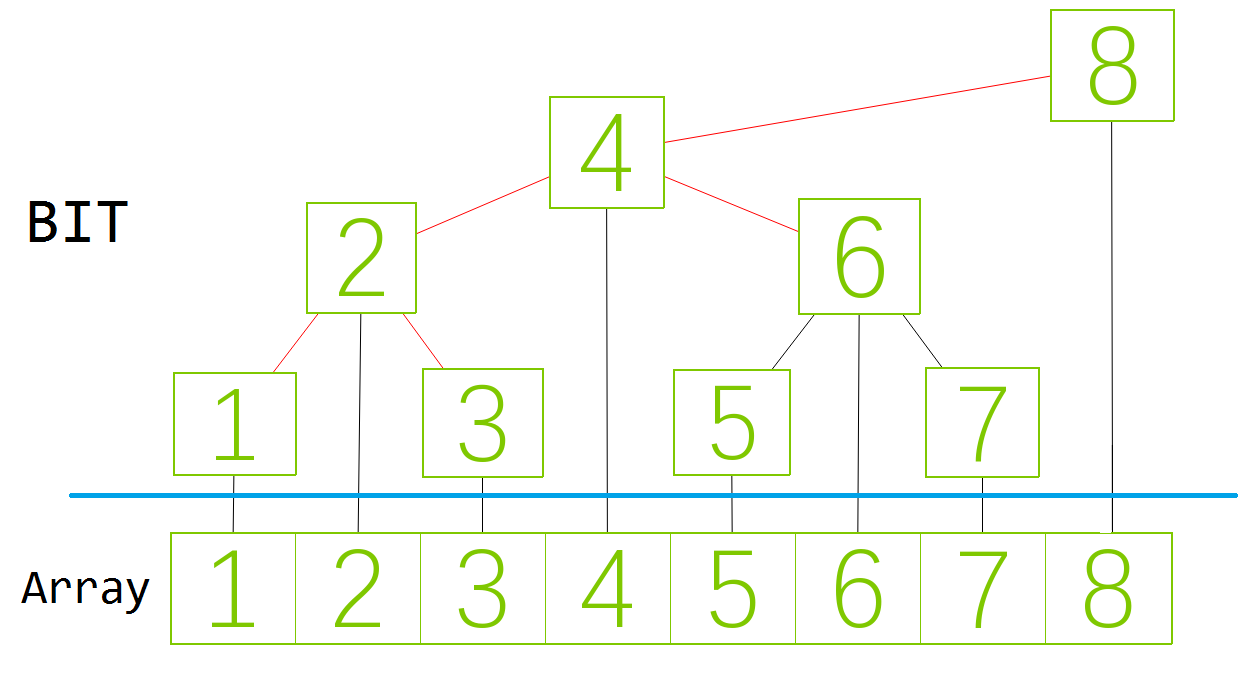
我们考虑将前缀和变为树形结构,使得其修改时只需要修改其祖先节点即可。
2. 树状数组
我们定义
其中 为 二进制末尾 的个数 .
我们可以发现:
| 二进制表示 | 区间 | |||||
|---|---|---|---|---|---|---|
表的最后一列表示了它们的递推关系。
其中下面是数组 ,上面是数组 .
不难发现, 就是这棵树的树高,显然二进制中末尾 的个数不会超过这个二进制的位数,所以树高是 的。
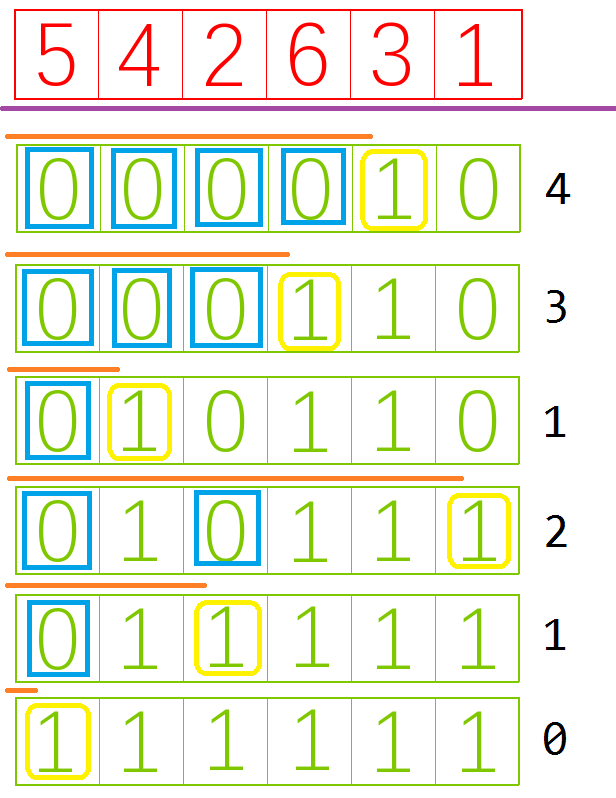
我们试着计算 (前缀和):
- 到 求和:, .
- 到 求和:, .
显然这个 的下标是每次 去掉末尾一个 后的值,这个值就是 n&(n-1) .
现在我们考虑 怎么计算。
先给结论:i&-i。
我们来验证一下:
- 显然当 时命题成立。
- 当 为奇数时:最后一位为 ,取反加 没有进位,故 和 除最后一位外前面的位正好相反,所以结果为 ,正确。
- 当 为二的次幂时:令 , 为整数。
显然 的二进制表示中只有最高位位是 ,故 取反加 后,从右到左第有 个 ,第 位及其左边全是 。这样结果是 ,正确。- 当 为偶数但不为二的次幂时:令 ,其中 为奇数(即其最低位为 )。
这时, 的二进制表示最右边有 个 ,从右往左第 位为 。当对 取反时,最右边的 个 变成 ,第 位变为 ;再加 ,最右边的 位就又变成了 ,第 位因为进位的关系变成了 。左边的位因为没有进位,正好和 原来对应的位上的值相反。二者按位与得到第 位上为 ,左边右边都为 的二进制数,即 ,正确。Q.E.D.
这个 其实也是 运算,即 ,显然 的下标也是 .
代码:
const int N=500005;
int n,m,a[N];
template<typename T>
struct BIT // 树状数组
{
private:
T s[N];
inline T lowbit(T x){return x&-x;}
public:
inline void build(T* arrb,T* arre){for (int i=0;arrb+i<arre;i++) add(i+1,*(arrb+i));} // 建立树状数组相当于 n 个单点修改
inline void build(T* arr,int end){for (int i=0;i<end;i++) add(i+1,arr[i]);}
inline void build(T* arr,int beg,int end){for (int i=beg;i<end;i++) add(i-beg+1,arr[i]);}
inline T query(T x) // 下面的这些操作的注释在「不封装的写法」里有
{
T ans=0;
while (x){ans+=s[x]; x-=lowbit(x);}
return ans;
}
inline T query(T l,T r){return query(r)-query(l-1);}
inline void add(int x,T now){if (x) while (x<=n){s[x]+=now; x+=lowbit(x);}}
};
// 不封装的写法:
const int N=500500;
typedef long long ll;
ll s[N];
int n,m;
inline int lowbit(int x){return x&(-x);} // lowbit
inline ll query(int x) // 区间查询,查询 1~x 的和,查询 l~r 的和时可以按照前缀和的方式减
{
int ans=0;
while (x){ans+=s[x]; x-=lowbit(x);} // ans 累加,x 每次去掉末位的 1
return ans;
}
inline void add(int x,ll now){while (x<=n){s[x]+=now; x+=lowbit(x);}} // x 每次加上末位的 1 就可以寻找祖先了
这里 query 函数和 add 函数的时间复杂度均为 .
2. 树状数组普通应用
1. 单点修改单点查询
这个直接用普通数组就行((((((((
2. 单点加区间求和
- 洛谷 P3374 【模板】树状数组 1
- loj #130. 树状数组 1 :单点修改,区间查询
上面讲过了
3. 区间加单点查询
- 洛谷 P3368 【模板】树状数组 2
- loj #131. 树状数组 2 :区间修改,单点查询
对 的区间修改时在树状数组的第 个位置加这个数,在 位置减这个数(差分)。
把这个数组做前缀和, 之间会加上这个数,到 的时候加减抵消,所以 没有影响。
这就把区间修改单点查询变成了两个单点修改加上一个区间查询了。
Code:
BIT<int> s;
void update(int l,int r,int x){s.add(l,x); s.add(r+1,-x);} // 在 l 处加这个数,r+1 处减这个数
int main()
{
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++)
{
scanf("%d",a+i);
s.add(i,a[i]-a[i-1]); // 建立
} int opt,l,r,k;
while (m--)
{
scanf("%d",&opt);
if (opt==1){scanf("%d%d%d",&l,&r,&k); update(l,r,k);}
else scanf("%d",&k),printf("%d\n",s.query(k)); // 查询时查询 1~k 的和即可
}
return 0;
}
4. 区间加区间求和
考虑对于一个前缀和做区间加(不妨设是加 ),它会变成这样:
显然这个新的前缀和如下:
我们维护两个数组 ,每次区间修改就只需要执行 ,,,(用差分)
这样 就是 了。
直接推比较困难,我们可以验证一下它的正确性:
- :显然正确
- :此时
- :此时
故正确。
Code:
BIT<ll> A,B; // 不开 long long 见祖宗
void update(int l,int r,int x){A.add(l,x*(1-l)); A.add(r+1,x*r); B.add(l,x); B.add(r+1,-x);}
int main()
{
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++){scanf("%d",a+i); A.add(i,a[i]);}
int opt,l,r,k;
while (m--)
{
scanf("%d",&opt);
if (opt==1){scanf("%d%d%d",&l,&r,&k); update(l,r,k);}
else
{
scanf("%d%d",&l,&r);
ll ans=A.query(r)+r*B.query(r)-A.query(l-1)-B.query(l-1)*(l-1); // 计算时的式子比较长
printf("%lld\n",ans);
}
}
return 0;
}
5. 树状数组求逆序对
- 洛谷 P1908 逆序对
首先先把数都丢到桶里,然后一个个从小到大加入树状数组,每次的前缀和就是比它小的数的数量,用 减一下就是逆序对的数量,累加一下即可。
Code:
ll ans;
void init()
{
for (int i=0;i<n;i++) tmp[i]=a[i];
sort(tmp,tmp+n); int c=unique(tmp,tmp+n)-tmp;
for (int i=0;i<n;i++)
a[i]=lower_bound(tmp,tmp+c,a[i])-tmp+1;
}
int main()
{
scanf("%d",&n);
for (int i=0;i<n;i++) scanf("%d",a+i); init();
for (int i=0;i<n;i++) s.add(a[i],1),ans+=i-s.query(a[i]);
printf("%lld",ans);
return 0;
}
3. 优化
1. 建树
树状数组的 建树思想简单来说就是把所有 的节点 () 累加到 中 .
Code 1(填表法):
for (int i=1;i<=n;i++)
{
scanf("%lld",s+i);
for (int j=1;j<lowbit(i);j*=2) s[i]+=s[i-j];
}
Code2(刷表法):
for (int i=1;i<=n;i++)
{
scanf("%lld",&x); s[i]+=x;
if (i+lowbit(i)<=n) s[i+lowbit(i)]+=s[i];
}
2. 时间戳优化
对付多组数据很常见的技巧。
如果每次输入新数据时都暴力清空树状数组,就可能会造成超时。
因此使用 标记,存储当前节点上次使用时间(即最近一次是被第几组数据使用)。每次操作时判断这个位置 中的时间和当前时间是否相同,就可以判断这个位置应该是 还是数组内的值。
3. 查询优化
树状数组查询区间和的方式是求前缀和,然后减,但是这种方法有些被重复计算了,并且和答案还没影响(因为被消掉了)。
稍微改改 query 即可优化:
int query(int l,int r)
{
l--; int sum=0;
while (r>l) sum+=a[r],r-=lowbit(r);
while (l>r) sum-=a[l],l-=lowbit(l);
return sum;
}
4. k 叉树状数组
1. 整数叉树状数组
比对:
| 二叉树状数组 | 三叉树状数组 | 叉树状数组 | ||
|---|---|---|---|---|
| 单点修改 | ||||
| 区间查询 |
我们看出,三叉树状数组的查询理论上比二叉树状数组慢,但修改更快一些。而在实际使用时,除了修改与查询一样多的题目,更多的是查询比修改多(毕竟只有查询有输出)。
所以,如果有 叉树状数组(),那么就能做到查询比二叉树状数组快。
这样,只能考虑 不为整数的情况。
2. 叉树状数组
区间树在某种意义上也可以构造出这样的结构:
这就是一棵以黄金分割(斐波那契数列)为基础的树状数组, .
虽然这样的树层数增多,影响修改的效率,但如果查询比修改多,这样的树状数组就能拥有理论上更小的常数。
3. 总结
我们也得到了这样的结论:
对于 叉树状数组, 越大,查询越慢,修改越快; 越小,查询越快,修改越慢。
当然,实际应用中还是最好用二叉树状数组,由于有位运算,所以二叉树状数组的代码量最少,而且实际常数往往更小。
而其他树状数组只能通过预处理一个数组来实现它们的类 lowbit 运算。
我们也同时发现树状数组和很多数据结构都有联系,其他很多数据结构实质是树状数组的变体,或树状数组是一些其他数据结构的结合:
- :暴力
- :分块
- :普通前缀和
4. 树状数组中级应用
1. 单点加区间最值
先建树:
for (int i=1;i<=n;i++)
{
cin>>a[i]; int pos=i;
while (pos<=n) c[pos]=max(c[pos],a[i]),pos+=lowbit(pos);
}
树状数组相当于一个前缀和,求和时可以用 ,但是最值没有这种减法的性质,所以这种建树每次查询前都必须初始化,时间复杂度难以接受,让我们换一种写法试一试:
for (int i=1;i<=n;i++)
{
cin>>c[i]; int t=lowbit(i);
for (int j=1;j<t;j*=2) c[i]=max(c[i],c[i-j]);
}
嗯, 建树的写法。
现在更新完某个数,之前的元素的值都是正确的了。
换了一种建树的方式就是为了维护 c 数组的正确性,修改同样也要保证 c 数组的正确性,那么在更新父亲节点时,我们就需要查询它所有的儿子节点,代码如下:
void add(int pos,int x)
{
a[pos]=x;
while (pos<=n)
{
c[pos]=x; int t=lowbit(pos);
for (int j=1;j<t;j<<=1) c[pos]=max(c[pos],c[pos-j]);
pos+=lowbit(pos);
}
}
这个 add 的时间复杂度是 的 .
查询操作:

假设当前查询的区间是 ,那么我们从 到 对每一个 数组的元素所控制的叶子节点进行判断。假设现在进行到了第 项,那么显然易得:该数控制的 数组的元素是 . 设 。如果 那么就将 加入最值的判断中,接着 ,否则的话就只对第 个元素加入,然后 ,代码如下:
int query(int l,int r)
{
int ans=a[r];
while (true)
{
ans=max(ans,a[r]); if (r==l) break; --r;
while (r-l>=lowbit(r)) ans=max(ans,c[r]),r-=lowbit(r);
}
return ans;
}
这个 query 也是 的。
2. 静态区间最值
见 https://www.zhihu.com/question/27919834/answer/39925959
3. 二维树状数组
加一维即可,EZ
5. 树状数组高级应用
1. 树状数组加 lazytag
毒瘤,咕咕咕
2. 可持久化树状数组
毒瘤,咕咕咕
3. 树状数组实现 BST 的功能
2022.1.18,更新了 .
和权值线段树做法本质相同吧 .
upd 2022/2/22. 好像不太一样
Reference
以下是博客签名,正文无关
本文来自博客园,作者:yspm,转载请注明原文链接:https://www.cnblogs.com/CDOI-24374/p/13873118.html
版权声明:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议(CC BY-NC-SA 4.0)进行许可。看完如果觉得有用请点个赞吧 QwQ



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】