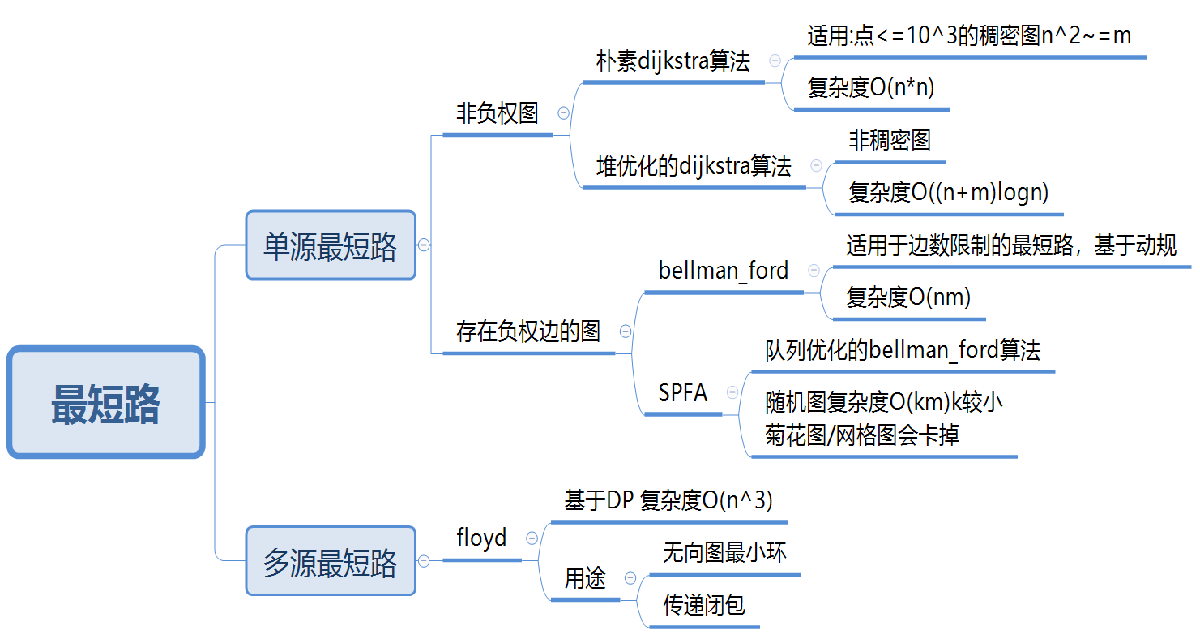
最短路算法

目录

• 1. 存图方法
  • 1.1 邻接矩阵
  • 1.2 vector 存图
  • 1.3 邻接表存图
• 2. 单源最短路径 - dijkstra
  • 2.1 算法描述
  • 2.2 题目
    • 2.2.1 Dijkstra 模板
    • 2.2.2 最短路的疑惑
    • 2.2.3 单词成语接龙
    • 2.2.4 聚会
    • 2.2.5 青蛙跳石头
• 3. 单源最短路径 - Bellman-ford
  • 3.1 算法描述
  • 3.1.5 优化
  • 3.2 题目
    • 3.2.1 K 边最短路
• 4 单源最短路径 - spfa
  • 4.1 算法描述
• 5 多源最短路径 - Floyd
  • 5.1 算法描述
• 6. 总结

若不加说明，所有的 \(n\) 都指点数，\(m\) 都指边数。

1. 存图方法

1.1 邻接矩阵

对于图 \(G(\mathbf{V,E})\)，维护矩阵 \(A\)，如果 \(u\to v\) 有一条边权为 \(w\) 的有向边则 \(A_{u,v}=w\)，若无边权则 \(A_{u,v}=1\)，若是无向图将 \(A_{v,u}\) 做同样处理。

空间复杂度 \(O(n^2)\) .
加边删边时间复杂度 \(O(1)\)；查询一个点的出边 \(O(n)\) .

适合稠密图，不适合稀疏图。

举例：

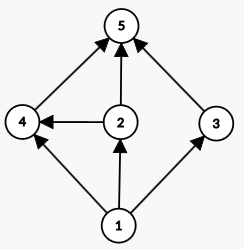
则此图对应的邻接矩阵为 \(A=\begin{bmatrix}0&1&1&1&0\\0&0&0&1&1\\0&0&0&0&1\\0&0&0&0&1\\0&0&0&0&0\end{bmatrix}\) .

代码实现：

const int N=5001; // 点数
int g[N][N];      // 邻接矩阵
inline void addedge(int u,int v,int w){a[u][v]=w;} // 加边 

---

1.2 vector 存图

对于图 \(G(\mathbf{V,E})\)，维护个 vector \(A_{1\dots n}\)，如果 \(u\to v\) 有一条有向边，那就在 \(A_u\) 处 push_back 一个 \(v\) 进去。如果边权为 \(w\) 就 push_back 进去一个 \(\text{pair}(v,w)\) .

空间复杂度 \(O(m)\) .
加边删边时间复杂度 \(O(1)\)（非常松的上界）；查询一个点的出边 \(O(m)\)（非常松的上界）.

举例：

还是这个图，用 vector 存会是这样：

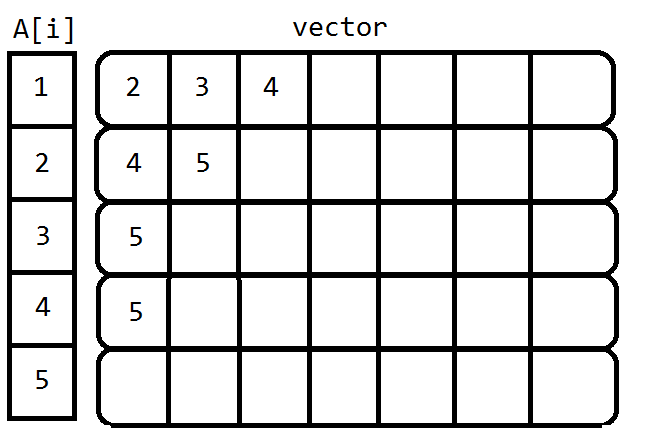
适合稀疏图。

代码实现：

const int N=5001; // 点数 
typedef vector<int> graph[N];
graph g;
inline void addedge(int u,int v,int w){g[u].push_back(make_pair(v,w);} // 加边 

---

1.3 邻接表存图

和 vector 存图类似，对于图 \(G(\mathbf{V,E})\)，维护个链表头序列 \(head_{1\dots n}\) 和 \(v_{1\dots n},w_{1\dots n}\)，表示去到的点和权值，如果 \(u\to v\) 有一条有向边，那就在 \(A_u\) 处 link 一个 \(idx\) 在后面，访问 \(v_{idx}\) 和 \(w_{idx}\) 即可查看边的信息。

因为方便所以加边时插在链表头的后面了。

时空复杂度和 vector 存图一样。

代码实现：

const int N=5001,M=10001; // 点数，边数
// v : ver
// w : val
// nxt 维护链表下一个 
int ver[M],nxt[M],head[N],val[N],tot=-1;
void addedge(int u,int v,int w){ver[++tot]=v; val[tot]=w; nxt[tot]=head[u]; head[u]=tot;}

// 遍历时用： 
for (int i=head[u];~i;i=nxt[i])
	// do something ...

---

---

2. 单源最短路径 - dijkstra

2.1 算法描述

单源最短路径是对于一个定点 \(u\)，求所有点 \(v\) 到 \(u\) 的最短路径。

定义 \(dis_v\) 为 \(u\) 到 \(v\) 的最短路径。

有两个集合 \(S\) 和 \(V\)，代表以及求完最短路的点和还没求完最短路的点，初始所有点都在 \(V\) 中。

算法流程：

1. 首先，\(dis_{u}=0\)，将 \(u\) 加入 \(V\) 中，对于任意点 \(\omega \neq u\)，\(dis_{\omega}=\infty\)。
2. 选取 \(V\) 中离 \(u\) 最近的点，并进行「松弛」操作，即对于 \(u\) 有直接连边的点 \(v\)，若 \(dis_v>dis_{u}+\mathrm{value}(u\to v)\)，则 \(dis_v := dis_u+\mathrm{value}(u\to v)\) .
3. 选取 \(S\) 中目前最小的 \(dis_i\) 加入 \(V\) 中（这步可以用小根堆优化）。
4. 若 \(V\) 中还有点，则重复执行 \(2,3\) 两步。

基于贪心的算法，因为多取一边长度更长在负权图下不成立，故 dijkstra 算法不能应用于负权图。

时间复杂度 \(O(m\log m)\) .

维基百科上的伪代码：

 1  function Dijkstra(Graph, source):
 2      dist[source]  := 0                     // Distance from source to source
 3      for each vertex v in Graph:            // Initializations
 4          if v ≠ source
 5              dist[v]  := infinity           // Unknown distance function from source to v
 6              previous[v]  := undefined      // Previous node in optimal path from source
 7          end if 
 8          add v to Q                         // All nodes initially in Q (unvisited nodes)
 9      end for
10      
11      while Q is not empty:                  // The main loop
12          u := vertex in Q with min dist[u]  // Source node in first case
13          remove u from Q 
14          
15          for each neighbor v of u:           // where v has not yet been removed from Q.
16              alt := dist[u] + length(u, v)
17              if alt < dist[v]:               // A shorter path to v has been found
18                  dist[v]  := alt 
19                  previous[v]  := u 
20              end if
21          end for
22      end while
23      return dist[], previous[]
24  end function

---

2.2 题目

2.2.1 Dijkstra 模板

时间限制：\(1\) 秒 内存限制：\(128\rm M\)

题目描述
罗老师被邀请参加一个舞会，是在城市 \(n\)，而罗老师当前所处的城市为 \(1\)，附近还有很多城市 \(2\sim n-1\)，有些城市之间没有直接相连的路，有些城市之间有直接相连的路，这些路都是双向的，当然也可能有多条。
现在给出直接相邻城市的路长度，罗老师想知道从城市 \(1\) 到城市 \(n\)，最短多少距离。

输入描述
第一行输入两个正整数 \(n,m\)，表示有 \(n\) 个城市和 \(m\) 条路；
接下来 \(m\) 行，每行三个正整数 \(u,v,w\)， 表示城市 \(u\) 与城市 \(v\) 有长度为 \(w\) 的路。

输出描述
输出 \(1\) 到 \(n\) 的最短路。如果 \(1\) 到达不了 \(n\)，就输出 -1。
输入输出样例
输入样例

5 5
1 2 20
2 3 30
3 4 20
4 5 20
1 5 100

输出样例

90

提示
数据规模和约定：\(1\le n \le 2000\)，\(1\le m \le 10^4\)，\(0\le w\le 10^4\) .

Dijkstra 板子。

Code：

#include<iostream>
#include<ctime>
#include<queue>
#include<stack>
#include<cmath>
#include<iterator>
#include<cctype>
#include<vector>
#include<map>
#include<set>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=2001,INF=0x3f3f3f3f;
typedef long long ll;
typedef vector<pair<int,ll> > graph[N];
graph g;
inline void addedge(int u,int v,ll w){g[u].push_back(make_pair(v,w));} // vector 存图
int n,m,s,dis[N]; // dis : 最短路数组
bool vis[N];      // vis : 标记，区分 S 集合和 V 集合
struct node       // node 结构体，存储一个点
{
	int idx,dis; // idx : 点的编号；dis : 点的最短路
	node(int _idx,int _dis){idx=_idx; dis=_dis;}
	inline bool operator<(const node& w)const{return dis>w.dis;}
};
inline void dij(int s) // 从 s 开始的最短路
{
	memset(dis,0x3f,sizeof dis);
	priority_queue<node> q; q.push(node(s,0)); dis[s]=0; // 初始 s
	while (!q.empty())
	{
		node now=q.top(); q.pop(); int nowi=now.idx,S=g[nowi].size(); // 最小的 dis[i]
		if (vis[nowi]) continue; vis[nowi]=true; // 判断集合
		for (int i=0;i<S;i++) // 松弛
		{
			int v=g[nowi][i].first,w=g[nowi][i].second; // 获取信息
			if (dis[nowi]+w<dis[v]){dis[v]=dis[nowi]+w; if (!vis[v]) q.push(node(v,dis[v]));} // 更新
		}
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for (int i=0,u,v,w;i<m;i++){scanf("%d%d%d",&u,&v,&w); addedge(u,v,w); addedge(v,u,w);}
	dij(1); printf("%d",(dis[n]-INF)?dis[n]:-1); // 如果 dis[n] 还是 ∞，那么说明无法到达点 n。
	return 0;
}
/*
5 5
1 2 20
2 3 30
3 4 20
4 5 20
1 5 100
*/

---

2.2.2 最短路的疑惑

时间限制：\(1\) 秒 内存限制：\(128\rm M\)

题目描述
丫丫在做最短路的时候，碰见了一位大佬，于是赶紧去 orz 了一番。之后大佬给了他一道最短路的题目，题目是这么说的：给定一张连通的非负权的有向图，求得 \(root\) 出发到达每个节点的最短距离，并将 \(root\) 中的所有可达节点的最短距离中的最大值设为当前图的直径。求得直径之后，将直径上的每个边进行修改，设当前图的直径的值为 \(A\)，对于该直径上的每一条边 \(e\)，如果该边 \(e\) 长度是奇数，则该边 \(e\) 加上 \(A\)，如果该边 \(e\) 是偶数则该边变为 \(A\)，对于生成的新图，请你求出新图下 \(root\) 的直径。

输入描述
第一行三个正整数 \(n,m,root\) 表示有 \(n\) 个点，\(m\) 条边,起点为 \(root\) . 接下来 \(m\) 行，每行三个整数 \(u,v,w\) ,表示 \(u\) 到 \(v\) 有一条权值为 \(w\) 的边。

输出描述
输出占一行，输出题目要求的新图的最短路。题目保证图的直径唯一。
样例输入输出
样例输入

4 3 2
2 3 4
3 4 1
4 1 2

样例输出

22

提示
数据范围与约定：\(1\le n\le 1000\)，\(1\le m\le 2\times 10^6\)，\(1\le w\le 1000\) .

考虑在更新时记录 \(pre_v=u\)，因为 \(v\) 是被 \(u\) 更新的，所以在路径中 \(v\) 一定在 \(u\) 的后面。

跑一边 dijkstra 找到最长的 \(dis_i\) 然后从 \(i\) 往前推顺便修改一下再跑一边 dijkstra 即可。

Code：

#include<iostream>
#include<ctime>
#include<queue>
#include<stack>
#include<cmath>
#include<iterator>
#include<cctype>
#include<vector>
#include<map>
#include<set>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=2001,INF=0x3f3f3f3f;
typedef long long ll;
typedef int graph[N][N]; // 图比较稠密，用的邻接矩阵。
graph g;
inline void addedge(int u,int v,ll w){g[u][v]=w;}
int n,m,s,dis[N],pre[N];
bool vis[N];
struct node
{
	int idx,dis;
	node(int _idx,int _dis){idx=_idx; dis=_dis;}
	inline bool operator<(const node& w)const{return dis>w.dis;}
};
inline void dij(int s)
{
	memset(dis,0x3f,sizeof dis);
	priority_queue<node> q; q.push(node(s,0)); dis[s]=0;
	while (!q.empty())
	{
		node now=q.top(); q.pop(); int nowi=now.idx;
		if (vis[nowi]) continue; vis[nowi]=true;
		for (int i=1;i<=n;i++)
			if (g[nowi][i])
			{
				int v=i,w=g[nowi][i];
				if (dis[nowi]+w<dis[v]){dis[v]=dis[nowi]+w; pre[v]=nowi; if (!vis[v]) q.push(node(v,dis[v]));} // 记录 pre
			}
	}
}
int main()
{
	scanf("%d%d%d",&n,&m,&s);
	for (int i=0,u,v,w;i<m;i++){scanf("%d%d%d",&u,&v,&w); addedge(u,v,w);}
	dij(s); int mmax=s,val=dis[mmax];
	for (int i=1;i<=n;i++)
		if ((dis[i]!=INF)&&(dis[i]>val)) mmax=i,val=dis[i]; // 找直径末尾
	while (mmax) // 直径末尾点 mmax 回推
	{
		int x=pre[mmax]; // 前驱
		if (!x) break;
		if (g[x][mmax]&1) g[x][mmax]+=val; // 更改
		else g[x][mmax]=val;
		mmax=pre[mmax]; // 回退
	}
	memset(vis,false,sizeof vis); memset(pre,0,sizeof pre);
	dij(s); mmax=s; val=dis[mmax];
	for (int i=1;i<=n;i++)
		if ((dis[i]!=INF)&&(dis[i]>val)) mmax=i,val=dis[i]; // 再次求直径
	printf("%d",val);
	return 0;
}
/*
4 3 2
2 3 4
3 4 1
4 1 2
*/

---

2.2.3 单词成语接龙

时间限制：\(1\) 秒 内存限制：\(128\rm M\)

题目描述
小可喜欢成语接龙和背单词。有一天他突发奇想，能否把汉语的成语接龙改成英语的单词接龙呢？小可看到手上的一堆纸牌，他在每个纸牌上都写上了一个长度 \(\ge 2\) 的单词，单词全部都是由小写字母构成的。小可想知道如果选择他的姓氏首字母 k 的单词作为首张牌，后面的每张牌的单词首字母必须与当前的牌的序列末尾的牌的字母末尾相等才可以衔接，至少需要几张牌可以完成以 d 为结尾的单词序列呢？
比如：

• kdy-yellod，长度 \(8\)，需要两张牌；
• kdy-yes-smald，长度 \(9\)，需要三张牌；
• kiss-smald，长度 \(8\)，需要两张牌。

因此最少需要两张牌，输出 \(2\)。

输入描述
第一行一个正整数 \(n\)，表示有 \(n\) 个单词。
接下来 \(n\) 行，每行一个由小写字母组成的单词。

输出描述
输出题目要求的结果。
如果不存在，输出 improssible。

样例
输入

5
kdy
yes
yellod
smald
kiss

输出

2

提示
数据规模与约定：\(2\le n \le 1000\)，单词长度在 \([2,100]\) 范围内。数据保证有首字母为 k 的单词。

对于一个单词 \(str\)，我们考虑只有首字母和末字母匹配的单词能连接，故将 \(str\) 的首字母与 \(str\) 的末字母连一条有向边。

然后从 d 跑一边 dijkstra 找一下 k 即可。

Code：

#include<iostream>
#include<ctime>
#include<queue>
#include<stack>
#include<cmath>
#include<iterator>
#include<cctype>
#include<vector>
#include<map>
#include<set>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=2001,INF=0x3f3f3f3f;
typedef long long ll;
typedef vector<pair<int,ll> > graph[N];
graph g;
inline void addedge(int u,int v,ll w){g[u].push_back(make_pair(v,w));}
int n,m,s,dis[N],pre[N];
bool vis[N];
struct node
{
	int idx,dis;
	node(int _idx,int _dis){idx=_idx; dis=_dis;}
	inline bool operator<(const node& w)const{return dis<w.dis;}
};
inline void dij(int s)
{
	memset(dis,0x3f,sizeof dis);
	priority_queue<node> q; q.push(node(s,0)); dis[s]=0;
	while (!q.empty())
	{
		node now=q.top(); q.pop(); int nowi=now.idx,S=g[nowi].size(); dis[nowi]=now.dis;
		if (vis[nowi]) continue; vis[nowi]=true;
		for (int i=0;i<S;i++)
		{
			int v=g[nowi][i].first,w=g[nowi][i].second;
			if (vis[v]) continue;
			if (dis[nowi]+w<dis[v]){dis[v]=dis[nowi]+w; pre[v]=nowi; q.push(node(v,dis[v]));}
		}
	}
}
inline int tonum(char q){return q-'a'+1;}
int main()
{
	scanf("%d",&m); n=26;
	for (int i=0;i<m;i++){string s; cin>>s; 
	addedge(tonum(*s.begin()),tonum(*(s.end()-1)),1);}
	dij(tonum('k'));
	if (dis[tonum('d')]!=INF) printf("%d",dis[tonum('d')]);
	else puts("improssible");
	return 0;
}
/*
4 3 2
2 3 4
3 4 1
4 1 2
*/

---

2.2.4 聚会

时间限制：\(1\) 秒 内存限制：\(128\rm M\)

题目描述
小 S 想要从某地出发去同学的家中参加一个 party，但要有去有回。他想让所用的时间尽量的短。但他又想知道从不同的点出发，来回的最短时间中最长的时间是多少，这个任务就交给了你。

输入描述
第一行三个正整数 \(n,m,k\)（\(n\) 是节点个数，\(m\) 是有向边的条数，\(k\) 是参加聚会的地点编号）
第 \(2\dots m+1\) 行每行 \(3\) 个整数 \(u,v,w\) 代表从 \(u\) 到 \(v\) 需要花 \(w\) 的时间。

输出描述
输出从不同的节点出发的最短时间中最长的时间。

样例输入输出
输入样例

4 8 2
1 2 4
1 3 2
1 4 7
2 1 1
2 3 5
3 1 2
3 4 4
4 2 3

输出样例

10

提示
数据范围与约定：\(1\le n\le 1000\)，\(1\le m\le 10^5\)，\(1\le w\le 100\)；数据中可能存在重边，保证聚会到其他点都是连通的。

去时直接跑最短路即可，回来时建反图（如果图 \(G\) 中有一条 \(u\to v\) 边权为 \(w\) 的有向边，那么反图 \(G_{rev}\) 中有一条 \(v\to u\) 边权为 \(w\) 的有向边）跑最短路即可。

Code：

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<map>
using namespace std;
const int N=1005;
typedef vector<pair<int,int> > graph[N];
graph g,rev; // rev 是反图
inline void addedge(graph g,int u,int v,int w){g[u].push_back(make_pair(v,w));} // 操作时加上 graph g 参数
int n,m,dis[N][N],sl[N],s;
bool vis[N];
struct node
{
	int idx,d;
	node(int ni=0,int nd=0){idx=ni; d=nd;}
	inline bool operator <(const node& a)const{return d>a.d;}
};
void dij(graph g,int s)
{
	memset(dis,0x3f,sizeof dis); memset(vis,false,sizeof vis);
	priority_queue<node> q; dis[s]=0; q.push(node(s,dis[s]));
	while (!q.empty())
	{
		int now=q.top().idx,S=g[now].size(); q.pop();
		if (vis[now]) continue;
		vis[now]=true;
		for (int i=0;i<S;i++)
		{
			int v=g[now][i].first,w=g[now][i].second;
			if (vis[v]) continue;
			if (dis[v]>dis[now]+w){dis[v]=dis[now]+w; q.push(node(v,dis[v]));}
		}
	}
}
int main()
{
	int ans=0,u,v,w;
	scanf("%d%d%d",&n,&m,&s);
	for (int i=0;i<m;i++){scanf("%d%d%d",&u,&v,&w); addedge(g,u,v,w); addedge(rev,v,u,w);}
	dij(g,s);
	for (int i=2;i<=n;i++) sl[i]=dis[i]; // 存储最短路数组
	dij(rev,s);
	for (int i=2;i<=n;i++) if (sl[i]+dis[i]!=0x3f3f3f3f) ans=max(ans,sl[i]+dis[i]);
	cout<<ans;
	return 0;
}

---

2.2.5 青蛙跳石头

时间限制：\(1\) 秒 内存限制：\(128\rm M\)

题目描述
一个池塘中分布着 \(n\) 块可以供青蛙跳跃的石头，坐标分别为 \((x_i,y_i)\)。给出青蛙 Freddy 和青蛙 Fiona 所在的石头，问如果 Freddy 想借助这 \(n\) 块石头跳到 Fiona 那里，那么它每次跳跃的距离最大值最小是多少？

输入描述
包含多组数据，每组数据第一行，一个整数 \(n\)，表示石头的个数。
接下来 \(n\) 行，每行两个数 \(x_i,y_i\) ，表示第 \(i\) 块石头的坐标，其中 \(1\) 号石头为 Freddy 的初始位置。\(2\) 号石头为 Fiona 的位置。每组数据之后有一个空行，\(n=0\) 时表示输入文件结束。

输出描述
每组输出占一行，输出对应的最小的距离最大值。结果保留三位小数。

输入输出样例
输入样例

2
0 0
3 4
3
17 4
19 4
18 5
0

输出样例

5.000
1.414

提示
数据范围与约定：\(2\le n\le 200\)，\(0\le x_i,y_i\le 1000\) .

对每个坐标 \((x_i,y_i)\) 变成一个点，每两点两两连边做 dijkstra 即可。

注意 dijkstra 时要维护一个最大值最小边，把 \(dis\) 数组的意义改变即可。

Code：

#include<iostream>
#include<ctime>
#include<queue>
#include<stack>
#include<cmath>
#include<iterator>
#include<cctype>
#include<vector>
#include<map>
#include<set>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=201;
typedef long long ll;
typedef vector<pair<int,ll> > graph[N];
graph g;
inline void addedge(int u,int v,ll w){g[u].push_back(make_pair(v,w));}
inline ll sqr(ll q){return q*q;} // 平方
inline ll dist(int x1,int y1,int x2,int y2){return sqr(x1-x2)+sqr(y1-y2);} // 距离的平方
int x[N],y[N],dis[N],q[N],tq[N];
bool vis[N];
struct node
{
	int idx,dis;
	node(int _idx,int _dis){idx=_idx; dis=_dis;}
	inline bool operator<(const node& w)const{return w.dis<dis;}
};
inline void dij(int s)
{
	memset(dis,0x3f,sizeof dis);
	priority_queue<node> q; q.push(node(s,0)); dis[s]=0;
	while (!q.empty())
	{
		node now=q.top(); q.pop(); int nowi=now.idx,S=g[nowi].size(); dis[nowi]=now.dis;
		if (vis[nowi]) continue; vis[nowi]=true;
		for (int i=0;i<S;i++)
		{
			int v=g[nowi][i].first,w=g[nowi][i].second;
			if (vis[v]) continue;
			if (max(dis[nowi],w)<dis[v]){dis[v]=max(dis[nowi],w); q.push(node(v,dis[v]));} // 松弛时要改变
		}
	}
}
inline int _hash(int x,int y){return x*1e4+y;} // 哈希，1e4 保险 
int main()
{
	int n;
	while (~scanf("%d",&n))
	{
		memset(vis,false,sizeof vis);
		if (!n) break;
		for (int i=0;i<n;i++) g[i].clear();
		for (int i=0;i<n;i++) scanf("%d%d",x+i,y+i),q[i]=tq[i]=_hash(x[i],y[i]);
		sort(tq,tq+n); int nown=unique(tq,tq+n)-tq;
		for (int i=0;i<n;i++) q[i]=lower_bound(tq,tq+nown,q[i])-tq; // hash 后离散化
		for (int i=0;i<n;i++)
			for (int j=0;j<n;j++)
				if (i!=j) addedge(q[i],q[j],dist(x[i],y[i],x[j],y[j])); // 完全图加边
		dij(0); // 下标从 0 开始
		printf("%.3f\n",sqrt(dis[1])); // 因为最大最小值的性质，所以最短路时维护距离的平方，输出时根号回去即可。
	}
	return 0;
}
/*
2
0 0
3 4
3
17 4
19 4
18 5
0
*/

---

3. 单源最短路径 - Bellman-ford

3.1 算法描述

考虑解决负权图单源最短路问题。

dijkstra 应用贪心思想，我们可以不应用贪心思想，维护 \(dp_{n,k}\) 为转移 \(k\) 次（至少走 \(k\) 条边）的第 \(n\) 点最短路径，然后暴力松弛即可。

转移方程很简单：

\[dp_{v,i}=\min\{dp_{v,i},dp_{u,i-1}+\mathrm{value}(u\to v)\}\qquad u,v\in \mathbf V\quad u\to v\in\mathbf E \]

显然，对于有负环且从源点可以到达的图，是不存在最短路径的（可以从负环一直走），如果最后了状态还能从自己转移那么表明存在负环，判一下即可。

时间复杂度 \(O(nm)\) .

3.1.5 优化

注意到每个点最坏情况下才需要 \(n-1\) 条边，标记一下是否转移然后跳出即可。

队列优化在第 4 节 spfa。

3.2 题目

3.2.1 K 边最短路

时间限制：\(1\) 秒 内存限制：\(128\rm M\)

题目描述
给定一个 \(n\) 个点 \(m\) 条边的有向图，图中可能存在重边和自环，边权可能为负数。请你求出从 \(1\) 号点到 \(n\) 号点的最多经过 \(k\) 条边的最短距离，如果无法从 \(1\) 号点走到 \(n\) 号点，输出 impossible。
注意：图中可能存在负权回路 。

输入描述
第一行包含三个整数 \(n,m,k\)。接下来 \(m\) 行，每行包含三个整数 \(u,v,w\)，表示存在一条从点 \(u\) 到点 \(v\) 的有向边，边长为 \(w\)。

输出描述
输出一个整数，表示从 \(1\) 号点到 \(n\) 号点的最多经过 \(k\) 条边的最短距离。如果不存在满足条件的路径，则输出 impossible。

样例输入输出
样例输入

3 3 1
1 2 1
2 3 1
1 3 3

样例输出

3

提示
数据规模与约定：\(1\le n,k\le 500\)，\(1\le m \le 10^4\)，任意边长的绝对值不超过 \(10000\) .

注意到 bellman-ford 过程中的 \(dp_{n,k}\) 就是答案，跑 bellman-ford 即可。

Code：

#include<iostream>
#include<ctime>
#include<queue>
#include<stack>
#include<cmath>
#include<iterator>
#include<cctype>
#include<vector>
#include<map>
#include<set>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=501,M=10001,K=501;
typedef vector<pair<int,int> > graph[N];
graph g;
inline void addedge(int u,int v,int w){g[u].push_back(make_pair(v,w));}
int dis[N][M],n,m,k;
/*
bool bellmanford(graph g,int s) 滚动数组版 bellman-ford 
{
	memset(dis,0x3f,sizeof dis);
	dis[s]=0; int t=0;
	for (int i=1;i<n;i++)
		for (int j=0;j<m;j++)
		{
			int u=a[j].u,v=a[j].v,w=a[j].w;
			if (dis[v]>dis[u]+w) dis[v]=dis[u]+w;
		}
	for (int i=0;i<m;i++)
	{
		int u=a[j].u,v=a[j].v,w=a[j].w;
		if (dis[v]>dis[u]+w) return false;
	} return true;
}*/
const int INF=0x3f3f3f3f;
struct Input{int u,v,w;}a[N];
void bellmanfordk(int s,int k) // 如果要优化必须留下最后一维（使用异或运算），如果压到一维的话状态一次可能转移多次，这样就得不到正确答案了（如果不是 k 边最短路的话是正确的） 
{
	memset(dis,0x3f,sizeof dis);
	for (int i=0;i<=n;i++) dis[s][i]=0;
	for (int i=1;i<=k;i++) // 到 k 即可 
		for (int j=0;j<m;j++)
		{
			int u=a[j].u,v=a[j].v,w=a[j].w;
			if (dis[v][i]>dis[u][i-1]+w) dis[v][i]=dis[u][i-1]+w;
		}
}
int main()
{
	scanf("%d%d%d",&n,&m,&k);
	for (int i=0;i<m;i++){scanf("%d%d%d",&a[i].u,&a[i].v,&a[i].w); addedge(a[i].u,a[i].v,a[i].w);}
	bellmanfordk(1,k);
	if (dis[n][k]>INF/2) puts("impossible"); // 负环会减少答案，所以要这么判（顺便判不连通了****） 
	else printf("%d",dis[n][k]);
	return 0;
}

4 单源最短路径 - spfa

4.1 算法描述

快速最短路算法（Shortest Path Fast Algorithm，SPFA）即 spfa .

显然 Bellman-ford 算法每次都需要遍历所有边，太慢了，有很多不需要松弛的边都被遍历了。注意到对于 \(u\to v\) 的一条有向边，当且仅当 \(d_u\) 被更新才可能 \(d_v\) 被松弛。

故建立一个队列，每次将队首顶点 \(u\) 取出，然后对从 \(u\) 出发的所有边 \(u\to v\) 进行松弛操作。若 \(v\) 不在队列中且在这一轮被松弛了，就将 \(v\) 加入队列，这样一直做即可。

显然最短路径最多经过 \(n-1\) 条边，所以如果入队次数超过 \(n-1\) 次就能判定有负环了。

5 多源最短路径 - Floyd

5.1 算法描述

Floyd 算法适用于 APSP（All Pairs Shortest Paths，多源最短路径），是一种动态规划算法，稠密图效果最佳，边权可正可负。此算法简单有效，由于三重循环结构紧凑，对于稠密图，效率要高于执行 \(|V|\) 次 Dijkstra 算法，也高于执行 \(|V|\) 次SPFA算法。

优点：容易理解，可算出任意两节点之间最短距离，代码简单。
缺点：时间复杂度较高，不适合计算大量数据。

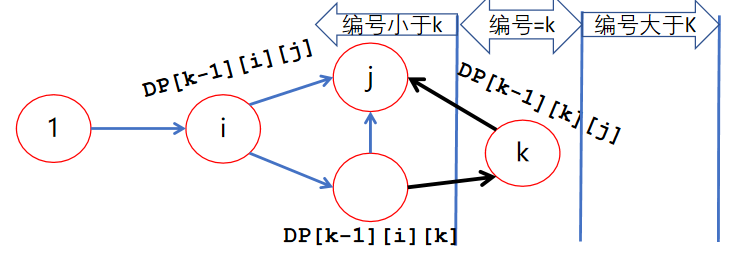
设 \(dp_{k,i,j}\) 表示经过若干编号不超过 \(k\) 的节点从 \(i\) 到达 \(j\) 的最短路长度。

转移：

1. 不经过k节点：\(dp_{k-1,i,j}\)
2. 经过k节点: \(dp_{k-1,i,k}+\)dp_{k-1,k,j}$

取个 \(\min\) 即可。

发现 \(dp_{k}\) 只与 \(dp_{k-1}\) 有关，所以可以滚动一维。

也就相当于 \(dp_{i,j}\) 是寻找一个中介点来转移。

6. 总结