数论 (1)
2022 年博主重读文章，发现有事实错误，语言表达也略欠缺，请理性对待文章内容（所以本文是议论文） .
本文数学公式较多，请耐心等待 .
好了，正片开始 .
- \(-1\) 前言
- \(0\) 带余除法
- \(1\) 整除
- \(2\) 同余
- \(2.1\) 定义
- \(2.2\) 性质
- \(2.3\) 拓展
- \(2.3.1\) 同余类、剩余系、简系与欧拉函数
- \(2.3.2\) 同余方程（组）
- \(2.3.2.1\) 定义
- \(2.3.2.2\) 性质
- \(2.3.2.3\) 算法
- \(2.3.2.3.0\) [前置] 拓展欧几里得算法 exgcd
- \(2.3.2.3.0\) [前置] 逆元/数论倒数
- \(2.3.2.3.0\) [前置] 阶
- \(2.3.2.3.0\) [前置] 原根
- \(2.3.2.3.1\) 形如 \(ax\equiv b\pmod m\) 的线性同余方程
- \(2.3.2.3.2\) 形如 \(a^x\equiv b\pmod m\) 的同余方程
- \(2.3.2.3.3\) 形如 \(x^a\equiv b\pmod m\) 的高次同余方程
- \(2.3.2.3.4\) 形如 \(\begin{cases}x\equiv a_1\pmod{m_1}\\x\equiv a_1\pmod{m_1}\\\dots\\x\equiv a_n\pmod{m_n}\end{cases}\) 的线性同余方程组
- \(3\) 数论函数
\(-1\) 前言
这里的例题大部分用的是洛谷上的。
\(0\) 带余除法
若 \(a,b\in \mathbb Z\)，我们将满足 \(bq\le a\) 的最大的 \(q\) 记做 \(a\) 除以 \(b\) 的商，实际上就是 \(\left\lfloor\dfrac{a}b\right\rfloor\)（\(\lfloor x\rfloor\) 指 \(x\) 向下取整），重点来了，对于这个 \(q\)，我们记 \(r=a-bq\) 为\(a\) 除以 \(b\) 的余数，一般记做 \(a\bmod b\)。
也就是我们小学学的：
\(1\) 整除
\(1.1\) 定义
若 \(a,b\in \mathbb Z\) 且存在 \(q\in \mathbb Z\) 使得 \(b=aq\)，则称 \(a\) 整除 \(b\)，记做 \(a\mid b\)。\(a\) 不整除 \(b\) 记做 \(a\nmid b\)
若 \(a,b\in \mathbb Z\) 且 \(a\mid b\)，则我们称 \(a\) 是 \(b\) 的约数/因数/因子，\(b\) 是 \(a\) 的倍数。
\(1.2\) 性质
-
\(a\mid b,b\mid c\Rightarrow a\mid c\)（传递性）。
-
\(a\mid b,a\mid c\Leftrightarrow \forall x,y\in \mathbb Z,a\mid bx+cy\)（线性组合）。
-
一些比较显然的其他性质：
- \(d\mid a\Rightarrow d\mid ka\)（\(k\in \mathbb Z\)）
- \(d\mid a,d\mid b\Leftrightarrow d\mid a\pm b\)
- \(a\mid b,b\mid a \Leftrightarrow a=b\)。
证明：
- 因 \(a\mid b\)，则存在 \(q_1\in \mathbb Z\) 使得 \(aq_1=b\)（定义），同理存在 \(q_2\) 使得 \(bq_2=c\)，代入得 \(aq_1q_2=c\)，即得 \(a\mid c\)。
- 先证引理
引理 1：\(a\mid b\Rightarrow a\mid bx\)
证明：由定义得存在 \(q\in \mathbb Z\) 使得 \(aq=b\)，代入，\(a\mid aqx\)，证毕。
引理 2：\(a\mid b\Rightarrow \forall x\in \mathbb Z,a\mid b+xa\)。
证明：由定义得存在 \(q\in \mathbb Z\) 使得 \(aq=b\)，代入，\(\forall x\in \mathbb Z,a\mid aq+xa\Rightarrow \forall x\in \mathbb Z,a\mid a(q+x)\)，证毕。
有了引理，命题就很显然了，先用1再用2就证出来了。
\(1.3\) 拓展
\(1.3.1\) 素数
\(1.3.1.1\) 定义
若一个正整数 \(q\) 只有 \(1\) 和 \(q\) 两个因子，则称 \(q\) 为素数（Prime）。
\(1.3.1.2\) 分解质因数/分解素因子
算术基本定理（唯一分解定理）：对于所有 \(a\in \mathbb N^+\)，\(a\) 均可被唯一的分解为 \(a=\prod\limits_{i=1}^O p_i^{r_i}\)，其中 \(p_i\) 均为素数，\(O\) 称为 \(a\) 的素因子个数，一般记为 \(\omega(a)\)，但是 OI 一般不会用到（指 \(\omega(a)\)）。
板子：洛谷 P2043。
\(1.3.1.3\) 算法
第一！朴素的 \(\mathcal O(\sqrt n)\) 判断素数：
bool Isprime(int n)
{
for (int i=2;i*i<=n;i++) // 因子是以 i,n/i 对称的，所以只需要枚举 [1,√n] 的数即可；并且注意 i=2 开始。
if (!(n%i)) return false; // !(n%i) == (n%i==0)，这句话的意思就是如果 i 是 n 的因子。
return true; // 没有其他因子，那么就是素数喽
}
第二！埃氏筛
我们考虑维护一个数组 isprime，然后直接把所有素数的倍数都标记为 false，判断时就可以直接 isprime[n] 了。
我们只需要遍历即可遍历所有素数（我们将 isprime[n]=false 的不进行筛，因为整除性），证明：
数学归纳法，\([2,2]\) 素数显然成立，如果目前把 \([2,n]\) 的素数都筛完了，那么如果 isprime[n+1]=false 成立；否则，如果它不是素数，那么它一定有一个 \([2,n-1]\) 之内的因子，但是如果它有这个因子早就被筛掉了，证毕。
gif 图片如下：
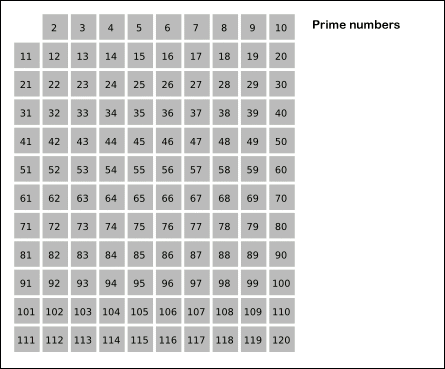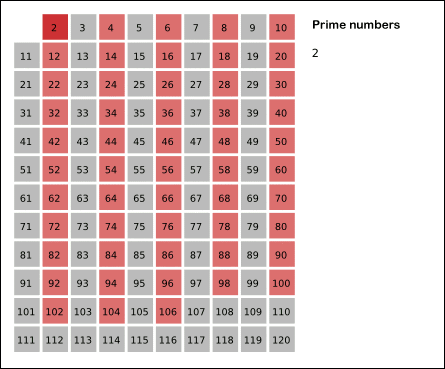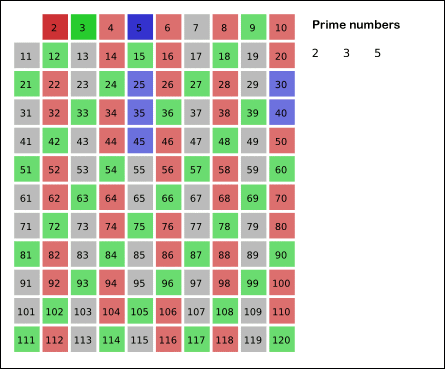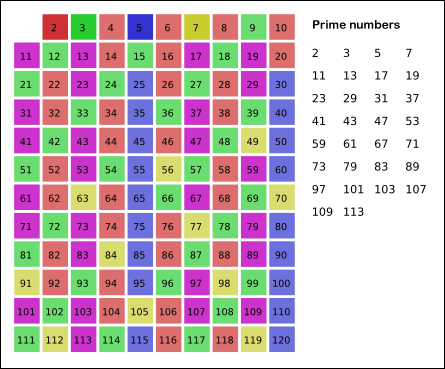
Code:
const int N=???;
bool isprime[N]; // 为了省去 memset，我们把 isprime[i]=false 当做其是素数。
int n; // 筛 1~n 素数
void GetPrime()
{
isprime[0]=isprime[1]=true;
for (int i=2;i*i<=n;i++) // 用 i*i 同上个算法。
{
if (isprime[i]) continue;
for (int j=i+i;j*j<=n;j+=i){isprime[j]=true;} // 筛
}
}
时间复杂度大约是 \(\mathcal O(n\log\log n)\)？因为 \(\log\log n\) 已经很接近 \(1\) 了，所以是近线性复杂度。
第三！真正线性的筛法！洛谷 P3383（模板）
这筛法还能顺便给个素数表。
核心：每个合数只被它最大的非自身的因数筛掉。
所以加上素数表，如果遇到素数直接 break; 即可。
const int N=???,M=???;
int prime[N],isprime[M],pi_; // pi_ 这个命名其实是表示 π(n) 函数
void GetPrime()
{
isprime[0]=isprime[1]=true;
for (int i=2;i<=n;i++)
{
if (!isprime[i]) prime[pi_++]=i;
for (int j=0;(j<pi_)&&(i*prime[j]<=N);j++) // j 用来枚举所有素数，我们都有素数表了就不用枚举了。
{
isprime[i*prime[j]]=1;
if (!(i%prime[j]))break; // Core!!!!!!!!!!!! 只筛一次！！！！！！！！！
}
}
}
MR 算法，仅供拓展。（判素用的，有点误差，但是复杂度接近 \(\mathcal O(1)\)），SPOJ288 -- PON Prime or Not 模板
一想到 \(\mathcal O(1)\)，我们不妨试一下随机算法。
按理来讲，我们应该是在 \([1,\sqrt n]\) 里面随机，再通过某些方式来提高正确率的。但是这样做太慢 QAQ，我们要确保每一个在 \([1,\sqrt n]\)
中的数都不是 \(n\) 的因子，显然用随机试的算法是行不通的。那么，我们该怎么办？
数论中，我们有 Fermat 小定理:
\(p\) 是素数 \(\Rightarrow x^p\equiv p\pmod p\)，即 \(x^{p-1}\equiv1\pmod p\)。
这个定理对于任何质数成立；但是反过来不一定。满足 Fermat 小定理的数不一定是质数。事实上，如果对任意\(b\in \mathbb{N},b^{p-1}≡1\pmod p\)，我们就称 \(p\) 为 Carmichael 数（伪 素 数）。运用 Fermat 小定理，我们可以判定一个数不是质数，但是不能判定一个数是质数（这个方法叫费马素性测试）。
不过，这给我们的随机枚举提供了一个不错的启示:不是随机枚举 \(n\) 的因子，而是一个基底 \(b\)。若对于不同的基底，都有\(b^{p-1}≡1\pmod p\)，\(p\) 是质数的可能性就更大了。事实上，如果 \(p\) 满足 \(b^{p-1}≡1\pmod p\)，那么 \(p\) 就叫做"基于 \(b\) 的伪素数"。
证明如下：
引入二次探测定理：
这个定理叫做“二次”是有原因的。其一，它是费马小定理探测质数的辅助工具，作为第二道屏障；其二，它和一个"二次同余方程"有关。定理如下:
若 \(x^2≡1\pmod p\)，则 \(x≡1\pmod p\) 或 \(x≡p-1\pmod p\)
这个定理比较好证明：
对于一个质数 \(p\)，只要 \(p\) 和二次探测定理不符，那么我们就可以肯定 \(p\) 不是质数、事实上，我们常常直接用这个定理去判定质数，而不是用费马小定理。
无论是费马小定理还是二次探测定理，我们都需要选取若干个合适的基底来进行测试。一般而言，我们会选取这五个基底： \(2,3,7,61,24251\)。当需要测试的数据规模在 \(10^{16}\) 左右时，它的表现效果还是可以的。但当数据规模更大些时，你必须考虑将基底扩大一些。在这个基底的基础上，可以考虑选取前 \(10\sim 15\)大的质数，从而解决几乎 \(100\%\) 的数据。
对于每一个基底 \(b\) 和一个待判断的数 \(x\)，我们进行如下测试：
- 用费马小定理判定一下这个数是不是合数。
- 如果 \(x-1\) 是偶数，我们可以对费马小定理做如下变形：
\(b^{x-1}≡1\pmod x\;\Rightarrow b^{\frac{x-1}2\times2}≡1\pmod x\)
这样就可以用二次探测定理看一下有没有 \(b^{\frac{x-1}{2}}≡1\) 或 \(x-1\pmod x\) 了。如果都不满足， \(x\) 就一定不是质数。
如果 \(\dfrac{x-1}{2}\) 同样是一个偶数，我们可以继续将它拆成 \(\dfrac{x-1}{4}\times 2\)，然后再用一次二次探测定理来做。
- 对于二次探测定理 \(X^k≡1\pmod x\) ，如果 \(k\) 是奇数或者 \(X≡x-1\pmod x\)，此时我们没有办法再拿这个数做文章了。我们只能暂时认定 \(x\) 是质数。
注意到这就是 Miller Rabin 算法具有随机性的证据之二：对质数的判定不充分。但事实上，用上面这种方法已经可以成功地判定许多质数了，在实际应用中是值得信赖的。
上面这个算法的时间复杂度是\(\mathcal O(\log^2 n)\)的：瓶颈在于快速幂和分解待验证的数；但实际运行时，速度是相当快的。
显然，我们不难看出上述代码有大量需要优化的地方。就比如说，开始的那次费马小定理的判定是完全没有必要的。我们可以直接把这一过程留到二次探测定理去执行。
其次，我们使用二次探测定理时每次都要探测 \(\log n\) 次，这个次数是可以稍微有所优化的。
对于前者，我们直接删去开头的费马小定理判断就可以了。对于后者，网上广为流传这样一种优化技巧:
设 \(k=x-1=2p?d\)，\(d\) 是一奇数，那么之前二次探测定理 \(X^2≡1\pmod x\) 检测的数 \(X\) 分别是如下几个数：\(b^{2^p\times d},b^{2^{p-1}\times d},b^{2^{p-2}\times d}，\dots,b^d\)。
如果我们从后往前检测，如果其中一个数 \(X\) 通过了二次探测定理，就直接判定 \(x\) 是质数。
这个新算法的流程如下:
- 按上面的方法计算出 \(d\) 和 \(p\)。记 \(cur=bd\)，如果 \(cur\equiv 1\) 或 \(x-1\pmod x\)就直接判定 \(x\) 是质数。
- 每次把 \(cur\) 赋值为 \(cur^2 \bmod x\)直到 \(cur=bk\)。这个过程等价与将 \(cur\) 从 \(bd\) 往 \(bk\) 的方向扫描。
- 如果 \(cur=x-1\) 则直接判定 \(x\) 为质数。否则转 \(2\)。
- 如果上述测试都没有判定 \(x\) 为质数，则直接判定 \(x\)为合数。
代码就不给了。
\(1.3.1.4\) 题目
因为因子对于 i,n/i 对称，再由于埃氏筛原理，应该每个数被按开关的次数就是 \(d(n)\)，因为对称，所以显然大多数 \(d(n)\) 是偶数，也就是最后是关着灯的。
当然，如果有一个 i 使得 \(i=\dfrac n i\)，它就是开着的那个灯了。
我们可以发现，这种 \(n\) 只有完全平方数且 \(i=\sqrt n\)。
Code:
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
int now=1,n;
cin>>n;
while (now*now<=n) cout<<now*now<<' ',now++;
return 0;
}
\(1.3.2\) GCD & LCM
\(1.3.2.1\) 定义
若 \(a_1,a_2\) 是两个不全为 \(0\) 的整数，若 \(d\mid a_1\) 且 \(d\mid a_2\)，我们则称 \(d\) 为 \(a,b\) 的公约数，我们将最大的 \(d\) 称为 \(a_1,a_2\) 的最大公约数（GCD），数学上一般记做 \((a_1,a_2)\)，OI 里一般记做 \(\gcd(a_1,a_2)\)。
若 \(\gcd(a_1,a_2)=1\)，则称 \(a_1,a_2\) 互素/互质（可以记做 \(a_1\perp a_2\)）。
若 \(a_1,a_2\) 是两个不全为 \(0\) 的整数，若 \(a_1\mid l\) 且 \(a_2\mid l\)，我们则称 \(l\) 为 \(a,b\) 的公倍数，我们将最小的 \(l\) 称为 \(a_1,a_2\) 的最小公倍数（LCM），数学上一般记做 \([a_1,a_2]\)，OI 里一般记做 \(\operatorname{lcm}(a_1,a_2)\)。
在这篇文章中，GCD 与 LCM 记做 \(\gcd(a,b)\) 与 \(\operatorname{lcm}(a,b)\)；而 \((l,r)\) 与 \([l,r]\) 表示区间。
\(1.3.2.2\) 性质
- 定理：对于 \(a,b\in\mathbb N^+\) ，我们找出 \(a,b\) 的质因数分解中相同的部分，然后算出它的值，就是 \(\gcd(a,b)\) 啦。
\(\text{ }\) \(\text{ }\) \(\text{ }\) \(\text{ }\) \(\text{ }\) 如果你把 \(\gcd(a,b)\) 只算一次，然后把 \(a,b\) 剩余的部分也加上，就是 \(\operatorname{lcm}(a,b)\) 喽。 - 显然，我们由
1得到了一个重要性质：\(\large \gcd(a,b)\operatorname{lcm}(a,b)=ab\)。 - 辗转相除：\(\gcd(a,b)=\gcd(b,a\bmod b)\)。
- 辗转相减（
其实叫「更相减损」的；和辗转相除同出一源）：\(\gcd(a,b)=\gcd(b,a-b)\)。
\(1.3.2.3\) 算法
计算 \(\gcd\) 与 \(\rm lcm\)：
// 辗转相除，O(log n) 的，用斐波那契数列的相邻两项能卡到 n^2。
int gcd(int a,int b){return b?gcd(b,a%b):a;} // 对于 b=0 辗转相除法是要特判的
int lcm(int a,int b){return a/gcd(a,b)*b;} // 套公式 gcd(a,b)*lcm(a,b)=a*b，改变了运算顺序防止爆掉 int
但是如果用高精的话（[SDOI2009] SuperGCD）就用更相减损术，减法比取模算的快。
\(1.3.2.4\) 题目
随便推推式子可知要最大化答案必须得寻找一个最小的 \(k\in \mathbb N^+\) 且满足 \(k\ge 6\) 且 \(k\mid n\) 然后用 \(n\) 除一下。
直接分解质因数大力计算即可。
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N=1e7+5;
int t,n,m,h,s[N];
int main()
{
// freopen("input.in","r",stdin);
cin>>t;
while (t--)
{
bool q=false;
cin>>n; h=0;
for (int i=1;i*i<=n;i++) // 分解
if (!(n%i)){++h; s[h]=i; ++h; s[h]=n/i;}
sort(s+1,s+1+h);
for (int i=h;i>=1;i--)
{
if (n/s[i]>5){cout<<s[i]<<'\n';q=true;break;}
} if (!q) cout<<"-1\n";
} // 反着来的
return 0;
}
众所周知 sin 用短直角边和斜边除一下就行了，也就是最短边除一下最长边。
约分同时约 \(\gcd\) 即可，放到例题里真没什么必要。
#include<iostream>
#include<algorithm> // <algorithm> 里面有 __gcd 直接求 GCD，但是 NOIP 不能用。
#include<cstdio>
using namespace std;
int main()
{
int a,b,c;
cin>>a>>b>>c;
cout<<min(a,min(b,c))/__gcd(min(a,min(b,c)),max(a,max(b,c)))<<'/'<<max(a,max(b,c))/__gcd(min(a,min(b,c)),max(a,max(b,c)));
return 0;
}
众所周知 \(\gcd(a,b)\rm lcm(\it a,b\rm)=\it ab\)，然后暴力即可。
#include<iostream>
using namespace std;
int gcd(int x,int y) {return y==0?x:gcd(y,x%y);}
int lcm(int x,int y) {return x*y/gcd(x,y);}
int main()
{
int x0,y0,s=0;
cin>>x0>>y0;
for (int p=1;p<=y0;p++)
for (int q=1;q<=y0;q++)
if (gcd(p,q)==x0&&lcm(q,p)==y0) s++;
cout<<s;
return 0;
}
取 \(\left\lfloor\dfrac nk\right\rfloor,2\left\lfloor\dfrac nk\right\rfloor,3\left\lfloor\dfrac nk\right\rfloor,\dots,k\left\lfloor\dfrac nk\right\rfloor\) 即可，显然这些数的 \(\gcd\) 是 \(\left\lfloor\dfrac nk\right\rfloor\)。
Code:
#include<iostream>
using namespace std; // n / k P r o b l e m
int main()
{
int n,k;
cin>>n>>k;
cout<<n/k;
return 0;
}
\(2\) 同余
\(2.1\) 定义
有 \(m\in \mathbb N^+\)，\(a,b\in \mathbb Z\)，若 \(m\mid a-b\)，则称 \(a\) 和 \(b\) 模 \(m\) 同余，记做 \(a\equiv b \pmod m\)。
其实就是 \(a\bmod m=b\bmod m\) 啦。
\(2.2\) 性质
- \(a\equiv b\pmod m\Rightarrow a\pm k\equiv b\pm k\pmod m \Rightarrow ak\equiv bk\pmod m\Rightarrow a^k\equiv b^k\pmod m\)（\(k\in \mathbb Z\) 且对于上述公式有意义）
- \(a\equiv b\pmod m,c\equiv d\pmod m\Rightarrow a\pm c\equiv b\pm d\pmod m\)
- 若 \(p\) 为素数，则 \(a^p\equiv a\pmod p\)，当且仅当 \(a\perp p\) 时，\(a_{p-1}\equiv 1\pmod p\)。
\(2.3\) 拓展
\(2.3.1\) 同余类、剩余系、简系与欧拉函数
\(2.3.1.1\) 定义
定义对于给定正整数 \(m\)，\(C_r=\{x\in \mathbb Z\mid x\equiv r\pmod m\}\) 。我们称 \(C_{0\dots m-1}\) 为模 \(m\) 的 同余类/剩余类，显然 \(C_{0\dots m-1}\) 构成 \(\mathbb Z\) 的一个划分。
取 \(a_i\in C_i\)，即可得到模 \(m\) 的一个完全剩余系 \(a\)，常用的是 \(1,2,\dots m-1\)，我们称其为模 \(m\) 的最小完全剩余系。
对于取的 \(a_i\perp m\) 的情况，\(a_i\) 称为模 \(m\) 的一个简系。
欧拉函数 \(\varphi(n)\) 是一个定义在正整数集上的函数，模 \(m\) 的一个简系的元素个数称为 \(\varphi(n)\)，也可称作 \(1\sim n\) 与 \(n\) 互素的数的个数（也可写作 \(0\sim n-1\) 与 \(n\) 互素的数的个数），可表示为 \(\varphi(n)=\sum\limits_{i=1}^{n}[i\perp n]\)。
\([x]\) 为条件符号，若 \(x\) 为真则返回 \(1\)，否则返回 \(0\)，相当于 bool(x)。
\(2.3.1.2\) 性质
剩余系什么的没啥性质，主要是欧拉函数。
- 若 \(m,n\) 互质，则 \(\varphi(nm)=\varphi(n)\varphi(m)\)（积性函数）
- 若 \(n\) 为奇数，则 \(\varphi(2n)=\varphi(n)\)。
- 通式：若 \(n=\sum\limits_{i=1}^s p_i^{a_i}\)，则 \(\varphi(n)=n\prod\limits_{i=1}^s\left(1-\dfrac{1}{p_i}\right)\)。
- 欧拉定理：若 \(a,m\in \mathbb N^+\)，\(a\perp m\)，\(m\ge 2\)，则 \(a^{\varphi(m)}\equiv 1\pmod m\)
- \(1\sim n\) 与 \(n\) 互素的数之和为 \(\dfrac12 n \varphi(n)\)。
- 对于任意正整数 \(n\)，\(\sum\limits_{d\mid n}\varphi(d)=n\)。
\(2.3.1.3\) 算法
首先当然是普通求 \(\varphi(n)\) 的算法：
// 第一种写法：暴力
// 时间复杂度：O(nlogn)
int phi(int n)
{
int ans=0;
for (int i=1;i<=n;i++) if (gcd(i,n)==1) ++ans; // gcd 这里没写
return ans;
}
// 第二种写法：套通式
// 时间复杂度：O(sqrt(n))
int phi(int n)
{
int ans=n;
for (int i=2;i*i<=n;i++) // 分解素因子
if(!(n%i))
{
ans=ans/i*(i-1);
while (!(n%i)) n/=i;
}
if (n>1) ans=ans/n*(n-1);
return ans;
}
线性筛欧拉函数（埃氏筛同理）。
根据欧拉函数和素因子的关系（通式），就仿照线性筛素数做就行。
const int N=???
int n,phi[N],prime[N],tot,ans;
bool isprime[N];
void getphi() // and prime???
{
phi[1]=1;
for (int i=2;i<=N;i++)
{
if (!isprime[i]){prime[++tot]=i; phi[i]=i-1;} // phi 一个素数答案显然是 n-1（2~n）
for (int j=1;j<=tot;j++)
{
if (i*prime[j]>N) break;
isprime[i*prime[j]]=1;
if (i%prime[j]) phi[i*prime[j]]=phi[i]*(prime[j]-1); // 这里用了欧拉函数的积性
else{phi[i*prime[j]]=phi[i]*prime[j]; break;}
}
}
}
\(2.3.1.4\) 题目
不难得出判定的写法是互质，然后随便推一下就会发现答案就是 \(2\sum\limits_{i=0}^{n-1}\varphi(i)+1\)。
主要是套板子，代码就不给了。
\(2.3.2\) 同余方程（组）
\(2.3.2.1\) 定义
设整系数多项式 \(f(x)=\sum\limits_{i=0}^na_ix^i\)，同余式 \(f(x)\equiv 0\pmod m\) 称为模 \(m\) 的同余方程，若整数 \(x_0\) 满足 \(f(x_0)\equiv 0\pmod m\)，则称 \(x_0\) 为同余方程的解。显然 \(x\equiv x_0\pmod m\) 都是同余方程的解，我们把它看做同余方程的 同一个解。
\(2.3.2.2\) 性质
- \(f(x)\equiv 0\pmod m\) 最多有 \(m\) 个解（显然）
- 若 \(f(x),g(x)\) 都是整系数多项式，\(f(x)\equiv 0\pmod m\Leftrightarrow f(x)+ms(x)\equiv 0\pmod m \Leftrightarrow f(x)+s(x)\equiv s(x)\pmod m\)
- 若 \(a\perp m\)，则 \(f(x)\equiv 0\pmod m\Leftrightarrow af(x)\equiv 0\pmod m\)。
\(2.3.2.3\) 算法
\(2.3.2.3.0\) [前置] 拓展欧几里得算法 exgcd
拓展欧几里得算法(exgcd)，可以用来找到形如 \(ax+by=\gcd(a,b)\) 的方程的一组特解。
由裴蜀定理知，原方程一定有解。
我们利用辗转相除法（普通欧几里得算法）。
我们设 \(d=\gcd(a,b)\)。
我们可以知道，我们辗转相除法的边界是 \(a=d,b=0\)，此时我们可以知道 \(a\) 就是最大公约数，我们还可以知道，在这时一定有一解为 \(x=1,y=0\)，即 \(1\times a+0\times b=d\)。
我们知道 \(\gcd(a,b)=\gcd(b,a\bmod b)\)，如果我们可以推导出每一次的解 \(x\) 和 \(y\)，与相除后的解 \(x'\) 和 \(y'\) 的关系；我们就可以算出其中的一个解了，（\(x\) 和 \(y\) 相当于是 \(a\) 和 \(b\) 的解，\(x'\) 和 \(y'\) 是 \(a\) 变成了 \(b\)，\(b\) 变成了 \(a\bmod b\) 时的解（辗转相除））。
轻易得知：
\(\begin{cases} ax+by=d\\ bx'+(a\bmod b)y'=d \end{cases}\)
则：
然后我们知道 \(x\) 与 \(x'\)， \(y\) 与 \(y'\)， 的关系后就可以求解了：
#include<iostream>
#include<cstdio>
using namespace std;
void exgcd(int a,int b,int& x,int& y) //x.y也可以用pair返回，这里用了引用
{
if (!b){x=1;y=0;return ;} //边界
gcd(b,a%b); //辗转相除
int tmp=y; y=x-(a/b)*y; x=tmp; //套公式
}
int main()
{
int a,b,x,y;
scanf("%d %d",&a,&b);
exgcd(a,b,x,y);
printf("%d %d",x,y);
return 0;
}
\(2.3.2.3.0\) [前置] 逆元/数论倒数
1.\(\,\)定义
我们称满足 \(aa^{-1}\equiv 1\pmod m\) 的 \(a^{-1}\) 称为 \(a\) 模 \(m\) 意义下的逆元（也叫数论倒数）。
逆元是模意义下的除法。
2.\(\,\)算法
普通求逆元用 exgcd 求解即可：
#include<iostream>
#include<cstdio>
using namespace std;
void exgcd(int a,int b,int& x,int& y) //拓展欧几里得
{
if (!b){x=1;y=0;return ;}
exgcd(b,a%b);
int tmp=x; x=y; y=tmp-a/b*y;
}
int main()
{
int a,b,x,y;
scanf("%d %d",&a,&b);
exgcd(a,b,x,y);
printf("%d",(x+b)%b);
return 0;
}
素数的逆元：众所周知，费马小定理是：
若 \(p\) 为素数，则 \(x^p\equiv x\pmod p\)。
当且仅当 \(x\nmid p\) 时：\(x^{p-1}\equiv 1\pmod p\)
然后我们用后面的式子同除以一个 \(x\)，可以得到 \(x^{-1}\equiv x^{p-2}\pmod p\)，所以我们只要求出 \(x^{p-2}\bmod p\) 就可以了，用快速幂求解即可。
Code:
#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;
ll qpow(ll x,ll y,ll mod) //快速幂
{
ll ans=1,base=x;
while (y)
{
if (y&1) ans*=base;
base*=base;y>>=1;
}
return ans;
}
int main()
{
ll x,p;
scanf("%lld %lld",&x,&p);
printf("%lld",qpow(x,p-2,p));
return 0;
}
线性筛逆元
线性筛肯定是 \(\mathcal O(n)\) 的嘛。
首先我们设 \(p=ki+r\)，然后可以知道 \(ki+r\equiv 0\pmod p\)（因为 \(ki+r=p\)，所以 \(p\bmod \;p=0\)）。
然后我们两边同乘 \(r^{-1}i^{-1}\)，就得到 \(kr^{-1}+i^{-1}\equiv 0\pmod p\)，移项得到 \(i^{-1}\equiv -kr^{-1}\pmod p\)。
我们可以知道 \(k=\left\lfloor \dfrac{p}{i}\right\rfloor,r=p\bmod\;i\)，所以我们得到公式：\(i^{-1}\equiv -\left\lfloor \dfrac{p}{i}\right\rfloor\times p\bmod \;i^{-1}\pmod p\)。
#include<iostream>
#include<cstdio>
using namespace std;
const int N=???;
typedef long long ll;
ll inv[N];
void GetInv(ll n,ll p)
{
for (int i=2;i<=n;i++)
inv[i]=(-(p/i)*inv[p%i]%p+p)%p;
}
线性筛阶乘逆元
也就是线性筛 \(n!^{-1}\)。
我们设 \(inv_i\) 表示 \(i!\) 的逆元，我们可以轻易知道 \(inv_{i+1}=\left(\dfrac{1}{i+1}\right)!^{-1}\)，我们同乘 \(i+1\) 就变成了，\(inv_{i+1}(i+1)=\left(\dfrac{1}{i!}\right)^{-1}=inv_i\)，所以我们可以得到：\(inv_{i+1}(i+1)=inv_i\)。
所以我们先求出 \(n!\) 的逆元，再倒推回来即可。
#include<iostream>
#include<cstdio>
using namespace std;
const int N=???
typedef long long ll;
ll inv[N];
void GetFactInv()
{
inv[1]=inv[0]=1;
for (int i=1;i<=n;i++) //求阶乘
inv[i]=(inv[i-1]*i)%p;
inv[n]=GetInv(inv[n],p); //求n!的逆元
for (int i=n-1;i>=1;i--)//倒推
inv[i]=(inv[i+1]*(i+1))%p;
return 0;
}
\(2.3.2.3.0\) [前置] 阶
定义：满足 \(a^x\equiv 1\pmod p\) 的最小正整数 \(x\) 称作 \(a\) 模 \(p\) 的阶，写作 \(\langle a \rangle\)（显然条件是 \(a\perp p\)）。
性质：
- \(\langle a \rangle\mid \varphi(p)\)
- \(a^0,a^1,a^2,\dots,a^{\langle a \rangle-1}\) 两两不同。
- \(a^x\equiv a^y\pmod p\) 的充要条件是 \(x\equiv y \pmod{\langle a \rangle}\)。
\(2.3.2.3.0\) [前置] 原根
定义：满足 \(g\) 关于模 \(p\) 的阶等于 \(\varphi(p)\) 的 \(g\) 是 \(p\) 的一个原根。
性质：
- \(g^r\equiv x\pmod p\) 的 \(r\) 是唯一的，反之亦然（\(g\) 是 \(p\) 的原根），\(x<p\)，\(r<\varphi(p)\)。
- 质数的原根个数是 \(\varphi(\varphi(p))\)。
- 一个模数存在原根的充要条件是，这个模数可以表示为\(1,2,4,p,2p,p^n\)其中 \(p\) 是奇质数，\(n\) 是任意正整数。
算法：考虑到最小的原根一般比较小，所以我们枚举原根然后判断。
假设我们当前枚举到 \(i\)，判断的时候只需要枚举 \(\varphi(p)\) 的质因子 \(p_{1\dots k}\)。然后判断 \(i^{\frac{\varphi(p)}{pj}}\) 是不是全部都不是 \(1\)，如果全部都不是 \(1\)，\(i\) 就是 \(p\) 的一个原根。
\(2.3.2.3.1\) 形如 \(ax\equiv b\pmod m\) 的线性同余方程
定理：
\(a,b\in \mathbb Z\)，一元一次同余方程 \(ax\equiv b\pmod m\) 有解的充要条件是 \(\gcd(a,m)\mid p\)，其解数为 \(\gcd(a,m)\)。
若 \(x_0\) 为其一解，那么他的 \(\gcd(a,m)\) 个解分别为 \(x\equiv x_0+\dfrac{m}{\gcd(a,m)}\times t\pmod m\)，其中 \(t=0,1,\dots,\gcd(a,m)-1\)。
读者自证不难（逃）。
有了后面这个关系就可以 exgcd 求所有解，比如 NOIp2012 提高组 洛谷 P1082 就是个 \(b=0\) 的特殊情况。
\(2.3.2.3.2\) 形如 \(a^x\equiv b\pmod m\) 的同余方程
当 \(a\perp m\) 时，使用 BSGS（北上广深 百事公司 Baby Step Giant Step 大步小步）算法，复杂度 \(\mathcal O(\sqrt p)\)：
设 \(x=pm-q\)，然后原式就成了 \(a^{pm}\equiv ba^q\pmod m\)，然后右边枚举 \(b\) 再用 hash 存起来（用 map 也不错），左边枚举 \(a\) 再一个个判即可。
// 核心代码
int m=sqrt(p)+1; Hash.Clear();
for (int i=0,t=z;i<m;++i,t=1ll*t*y%p) Hash.Insert(t,i);
for (int i=1,tt=fpow(y,m,p),t=tt;i<=m+1;++i,t=1ll*t*tt%p)
{
int k=Hash.Query(t);
if (k==-1) continue;
printf("%d\n",i*m-k);return ;
}
对于 \(a\not\perp m\)（？？？）时，使用 exBSGS 算法：
令 \(d=\gcd(y,p)\)，然后将方程改成等式 \(a^x+kp=b\)，注意到 \(b\) 必须是 \(d\) 的倍数否则无解，所以除一下 \(d\) 得 \(\dfrac ada^{x-1}+k\dfrac pd=\dfrac bd\)，然后无限迭代成 \(\dfrac{y^k}dy^{x-k}\equiv \dfrac bd\pmod{\dfrac pd}\)，所以 BSGS 求一下在还原回去即可。
// 核心代码
void ex_BSGS(int y,int z,int p)
{
if (z==1){puts("0");return;}
int k=0,a=1;
while (19260817) // 变换
{
int d=__gcd(y,p);if(d==1)break;
if (z%d){NoAnswer(); return ;}
z/=d;p/=d;++k;a=1ll*a*y/d%p;
if (z==a){printf("%d\n",k); return ;}
}
Hash.clear();
int m=sqrt(p)+1; // BSGS
for (int i=0,t=z;i<m;++i,t=1ll*t*y%p) Hash.Insert(t,i);
for (int i=1,tt=fpow(y,m,p),t=1ll*a*tt%p;i<=m;++i,t=1ll*t*tt%p)
{
int B=Hash.Query(t);
if (B==-1) continue;
printf("%d\n",i*m-B+k); return ;
}
NoAnswer();
}
\(2.3.2.3.3\) 形如 \(x^a\equiv b\pmod m\) 的高次同余方程
this，目前看不懂，等看懂了补上。
\(2.3.2.3.4\) 形如 \(\begin{cases}x\equiv a_1\pmod{m_1}\\x\equiv a_1\pmod{m_1}\\\dots\\x\equiv a_n\pmod{m_n}\end{cases}\) 的线性同余方程组
\(3\) 数论函数
一般地，可把数论函数看做是整数集上定义的函数。
\(3.1\) 积性函数与完全积性函数
\(3.1.1\) 定义
若 \(f\) 是一个数论函数，且对于任意 \(a\perp b\) 均有 \(f(ab)=f(a)f(b)\)，则称 \(f\) 为积性函数。
若 \(f\) 是一个数论函数，且对于任意 \(a,b\) 均有 \(f(ab)=f(a)f(b)\)，则称 \(f\) 为完全积性函数。
\(3.1.2\) 性质
由唯一分解定理知，对于任意积性函数 \(f\) 一定可以表示为 \(f(x)=\prod\limits_{i=1}^{\omega(x)}{p_i^{a_i}}\)，其中 \(p_1^{a_1}p_2^{a_2}\dots\) 是 \(x\) 的标准分解（然后就可以直接转换递归做了）。
\(3.2\) 一些特殊数论函数
\(3.2.1\) 素数计数函数 \(\pi(n)\)
\(3.2.1.1\) 定义
素数计数函数 \(\pi(n)\) 为不超过 \(n\) 的素数个数，即 \(\pi(n)=\sum\limits_{i=1}^n[i\text{ is a prime}]\)。
\(3.2.2\) 单位函数 \(\epsilon(n)\)
\(3.2.2.1\) 定义
\(\epsilon(n)=[n=1]\)，也就是 \(\epsilon(n)=\begin{cases}1&n=1\\0&\text{otherwise.}\end{cases}\)
显然，单位函数是完全积性函数。
\(3.2.3\) 除数函数 \(\sigma_k(n)\)
\(3.2.3.1\) 定义
\(\sigma_k(n)\) 就是 \(n\) 的所有因子的 \(k\) 次方和，即 \(\sigma_k(n)=\sum\limits_{d\mid n}d^k\)。
特殊的，\(\sigma_0(n)\) 为 \(n\) 的因数个数，常记做 \(d(n)\)；\(\sigma_1(n)\) 为 \(n\) 的因数和，常记做 \(\sigma(n)\)。
除数函数是积性函数。
\(3.2.4\) 欧拉函数 \(\varphi(n)\)
前面同余讲了
\(3.2.5\) 函数 \(I(n)\)、幂函数 \(\operatorname{Id}_k(n)\) 与莫比乌斯函数 \(\mu(n)\)
定义 \(I\) 为取值常为 \(1\) 的函数，定义幂函数 \(\operatorname{Id}_k(n)=n^k\)，对于 \(k=1\) 时，\(\operatorname{Id}_1\) 常记做 \(\operatorname{Id}\)。
莫比乌斯函数 \(\mu(n)\) 将在章节「\(3.4\) 莫比乌斯函数与莫比乌斯反演」处展开。
\(\mu(n)\) 是积性函数。
\(3.3\) 狄利克雷（Dirichlet）卷积
\(3.3.1\) 定义
若 \(f,g\) 为数论函数，则我们称 \(f\) 和 \(g\) 的 Dirichlet 卷积 \(f*g=\sum\limits_{ij=n}f(i)g(j)=\sum\limits_{d\mid n}f(d)g(\dfrac nd)\)，后面那个是一般用的表示形式。
\(3.3.2\) 性质
- 交换律：\(f*g=g*f\)。
- 结合律：\(f*g*h=f*(g*h)\)。
- 分配律：\(f*h+g*h=(f+g)*h\)。
- 结合律 II：\((xf)*g=x(f*g)\)（\(x\) 是一个系数）
- 单位元：\(\epsilon*f=f\)。
\(3.3.3\) 有趣的性质
- \(\sigma_k=1*\operatorname{Id}_k\)
- \(\operatorname{Id}=\varphi*1\)
- \(d=1*1\)
- \(\varphi=\mu*\operatorname{Id}\)。
\(3.3.4\) 题目
给定 \(n\)（\(1\le n \le 2^{32}\)），求 \(\sum\limits_{i=1}^n\gcd(i,n)\)。
简单推式题：
\(3.4\) 莫比乌斯函数与莫比乌斯反演
\(3.4.1\) 莫比乌斯函数 \(\mu(n)\)
\(3.4.1.1\) 定义
莫比乌斯函数 \(\mu(n)=\prod\limits_{p\in \rm Prime}(-1)^{[p\mid n]}[p^2\nmid n]\)，但是主流的定义好像是 \(\mu(n)=\begin{cases}1&n=1\\(-1)^s&n=\prod\limits_{i=1}^sp_i&(p_i\in \rm Prime)\\0&\rm otherwise.\end{cases}\)
\(3.4.1.2\) 性质
-
\(\mu(n)\neq 0\) 当且仅当 \(n\) 无平方因子。
-
\(\mu\) 是积性函数（前面有）
-
\(\mu*1=\epsilon\)
\(3.4.1.3\) 算法
线性筛
void getMu() {
mu[1] = 1;
for (int i = 2; i <= n; ++i) {
if (!flg[i]) p[++tot] = i, mu[i] = -1;
for (int j = 1; j <= tot && i * p[j] <= n; ++j) {
flg[i * p[j]] = 1;
if (i % p[j] == 0) {
mu[i * p[j]] = 0;
break;
}
mu[i * p[j]] = -mu[i];
}
}
} //OI wiki
\(3.4.2\) 莫比乌斯反演
\(3.4.2.0\) [前置] 数论分块
以下是博客签名，正文无关
本文来自博客园，作者：Jijidawang，转载请注明原文链接：https://www.cnblogs.com/CDOI-24374/p/13378405.html
版权声明：本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议（CC BY-NC-SA 4.0）进行许可。看完如果觉得有用请点个赞吧 QwQ
