浅谈 LCA

LCA（Least Common Ancestors），最近公共祖先，定义为两节点最近的公共祖先好像是废话

前置芝士：

• 图论

此文章中均设 \(\mathrm{fa}_i\) 为 \(i\) 的父亲，\(\mathrm{dep}_i\) 为 \(i\) 的深度。

暴力

显然我们找出节点的所有祖先再 \(n^2\) 比较即可。

当然你也可以一层层往上跳。

时间复杂度是 \(\mathcal{O}(n^2)\)。

倍增

我们思考一次性跳多步，减少时间复杂度。

考虑二进制拆分。

考虑用 dp 预处理：

设 \(f_{i,j}\) 为 \(i\) 往上跳 \(2j\) 步到达的点，即可以使用以下转移方程：

\(\begin{cases} f_{i,0}=\mathrm{fa}_i\\ f_{i,j}=f_{f_{i,j-1},j-1} \end{cases}\)

所以我们设 \(\mathrm{lg2}_k=\lfloor\log_2k\rfloor\)，即 直接从 \(\mathrm{lg2}_i\) 往下枚举即可。

---

整理下，如果我们求 \(\mathrm{LCA}(u,v)\)：

默认 \(\mathrm{dep}_u<\mathrm{dep}_v\)（如果不满足根据 \(\mathrm{LCA}(u,v)=\mathrm{LCA}(v,u)\) 交换 \(u,v\) 即可）

过程如下：

1. 预处理 \(f\) 数组
2. 将 \(u,v\) 跳至同一层
3. 如果相等直接返回
4. 否则继续跳，直到它们都跳到 LCA 的往下一层。

这个在链上极其好用。

代码：

int LCA(int u,int v)
{
	if (dep[u]<dep[v]) swap[u][v]; //交换
	while (dep[u]>dep[v])          //预处理
		u=fa[u][lg2[dep[u]-dep[v]-1]];
	if (u==v) return u;            //跳出
	for (int i=lg2[dep[u]-1];i>=0;--i)
		if (fa[u][i]!=fa[v][i])
			u=fa[u][i],v=fa[v][i]; //继续跳
	return fa[u][0];
}

RMQ求解

RMQ（Range [Minimum/Maximum] Query），区间最值问题。

首先我们要了解一个离线求 RMQ 的数据结构——st表（Sparse Table）

因为 st 表也是倍增思想，所以转移方程也会很像：

• 设 \(f_{i,j}\) 表示 \(i\) 开始，\(2j\) 个元素的最值（不一定连续）

• 则 \(f_{i,j}=\min(\mathrm{or}\;\max)(f_{i,j-1},f_{i+2^{j-1},j-1})\)（切开求解）

首先考虑最值允许区间重叠：

\[\max(a,b,c)=\max(\max(a,b),\max(b,c)) \]

我们即肯定能找到一个 \(x\) 使得 \([l,l+2^x-1]\) 和 \([r-2^x+1,r]\) 的最值与 \([l,r]\) 的最值相等。

则这个 \(x\) 很容易想出（\(l,r\) 之间有 \(r-l+1\) 个元素）：

\[\large x=\log_2(r-l+1) \]

---

我们回归 LCA。

首先我们要了解欧拉序。

以此图为例：

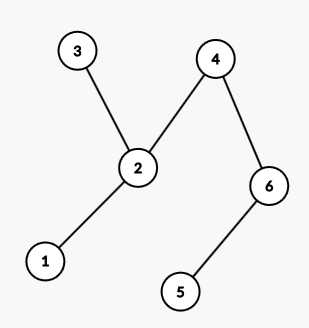
设 \(4\) 为树根：

则它的属性：

• DFS 序：\(4,2,3,1,6,5\)；
• 带上回溯的 DFS 序：\(4,2,3,2,1,2,4,6,5,6,4\)。

其中“带上回溯的 DFS 序”即为欧拉序。

---

我们看看此图：

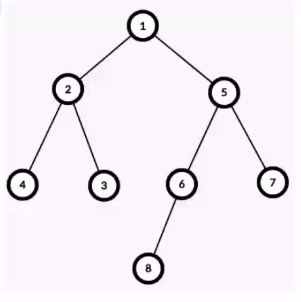
比如我们找 \(4,8\) 的 LCA：

写出欧拉序：

\[1,2,4,2,3,2,1,5,6,8,6,5,7,5,1 \]

转换为深度：

\[1,2,3,2,3,2,1,2,3,4,3,2,3,2,1 \]

找出 \(4,8\) 之间区域：

\[1,2,\bold{3,2,3,2,1,2,3,4},3,2,3,2,1 \]

正好深度最低的点就是 \(1\)，它们的 LCA！

这样就把 LCA 转换为了 RMQ，st表求解即可。

Tarjan 算法

我们引用 rxz 的话：

一个熊孩子 Link 从一颗有根树的最左下节点灌岩浆，Link 表示很讨厌这种倒着长的树，岩浆会不断蔓延到整个树。

如果岩浆灌满了一颗子树 Link 发现树的右边有棵更深的子树，则 Link 会去灌岩浆。

岩浆只有迫不得已的情况才会升高，找新子树进行注入。

机(yu)智(chun)的 Link 发现了一个求 LCA 的好办法，即：如果两个节点都被岩浆烧掉时，它们的 LCA 即为那棵子树上岩浆最高的位置。

即按 rxz 描述的写即可，伪代码如下：

void tarjan()
{
	for (u的所有儿子v)
    {
		tarjan(v);
        merge(u,v); //并查集
    }
    for (所有与u有关的查询(u,v))
    	if (vis[v]) ans[id]=find(v);
}

树剖写法

树剖，即树链剖分，将树变为链的方法，可以应对某些毒瘤出题人将数列上问题转移到树上的情况。

我们求 LCA 用的是轻重链剖分，也就是将树变成轻链和重链。

我们首先给出一些定义：

• 重儿子：某节点儿子中子树最大的儿子（相等随便选一个）
• 轻儿子：除重儿子以外的所有儿子
• 重边：爹连到重儿子的边（爹不一定是重儿子）
• 轻边：除重边外所有边
• 重链：重边组成的链（轻叶节点自成重链）
• 轻链：轻边组成的链

我们树剖需要的数组：

• \(\mathrm{siz}_i\) 表示以 \(i\) 为根的子树大小。
• \(\mathrm{hvs}_i\) 表示 \(i\) 节点的重儿子。
• \(\mathrm{ltp}_i\) 表示 \(i\) 所在的重链头（深度最浅节点）。

树刨和莫队等等一样都是优雅的暴力 ，会被轻重链交替的数据或者全是轻链的数据卡死。

首先两次 DFS：

• 第一次求 \(\mathrm{fa}\)、\(\mathrm{dep}\)、\(\mathrm{siz}\)、\(\mathrm{hvs}\)。
• 第二次只求 \(\mathrm{ltp}\)。

然后轻重链交替跳 LCA 即可（适时原 地 踏 步）。