浅谈排序算法[动图]
本文只是介绍多种排序思想及代码，具体实现细节将不会提及
内部排序
内部排序主要是在OI中可以使用，外部排序则不能。
下面我们将讲述\(21\)种内部排序，请做好准备。
1.内省式排序
其实是多种排序算法的集合，先进行快速排序，如果序列接近有序或比较小用插入排序，如果递归层数过多则改用堆排序。
你有没有想：一开始就介绍这么多种排序算法的集合，还没学那些排序呢！
不用担心，这个东西的实现代码最简单：
sort(arr,arr+n);
如果想要逆序排序或者其他规则排序：
#include<algorithm> //一定要用这个头文件
bool cmp(obj a,obj b) //obj指你要排序对象的类型
{
... //里面的规则如果写return a<b;就是从小到大啦，sort默认从小到大。
return ...;
}
sort(arr,arr+n,cmp);
2.冒泡排序
冒泡就是先遍历数组1~n-1的元素，如果a[i]>a[i+1]就把他们交换，然后遍历数组2~n-1的元素\(\dots\)最后遍历到n-1~n-1结束。
动图如下：
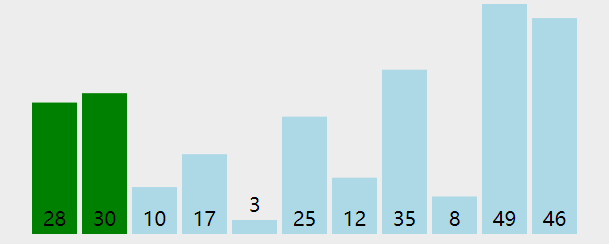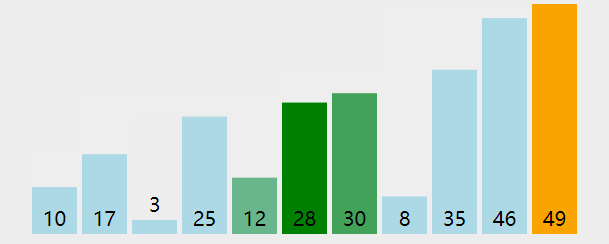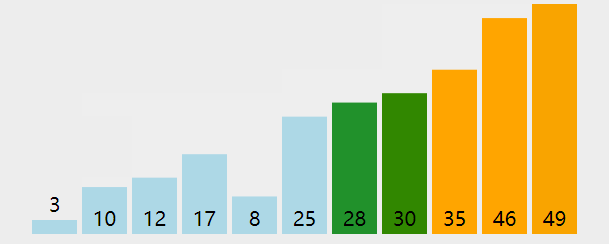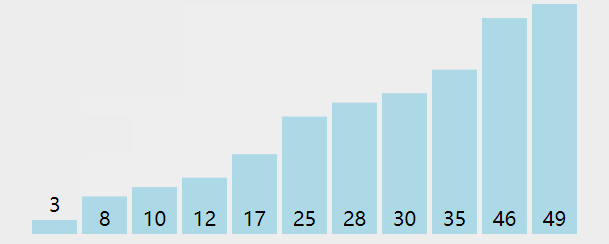
效果图（可视化感觉更强）：
代码如下：
template<typename T>
void BubbleSort(T arr[], T n)
{
for (int i=0;i<n-1;i++)
for (int j=0;j<n-i-1;j++)
if (arr[j]>arr[j+1])
{
T temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
还可以加个优化，如果没有交换发生（以及有序）就不用再遍历了：
template<typename T>
void BubbleSort(T arr[], T n)
{
for (int i=0;i<n-1;i++)
for (int j=0;j<n-i-1;j++)
{
bool flag=false;
if (arr[j]>arr[j+1])
{
T temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
flag=true;
}
if (!flag) return ;
}
}
时间复杂度\(\mathcal{O}(n^2)\)
3.[冒泡排序优化]鸡尾酒排序
鸡尾酒排序，也就是定向冒泡排序，鸡尾酒搅拌排序，搅拌排序（也可以视作选择排序的一种变形），涟漪排序，来回排序或快乐小时排序，是冒泡排序的一种变形。
这个算法不是单纯的单向排序了，而是第一次从左到右冒泡，第二次从右到左冒泡\(\dots\)
这样的话会优化常数，但还是\(\mathcal{O}(n^2)\)
动图：
代码如下：
void Cocktailsort(int s[],int n)
{
int left=0;
int right=n-1;
while(left<right)
{
for(int i=left;i<right;i++)
if (s[i]>s[i+1]) swap(s[i],s[i+1]);
right--;
for(int i=right;i>left;i--)
if(s[i]<s[i-1]) swap(s[i],s[i-1]);
left++;
}
}
鸡尾酒排序也可以加优化：判断是否产生交换，代码并不难写，读者可以自己实现。
4.[冒泡排序优化]地精排序
被Dick Grune称为最简单的排序算法。整个算法只有一层循环，默认情况下前进冒泡，一旦遇到冒泡的情况发生就往回冒，直到把这个数字放好，然后继续前进，前进到数组最后一个数结束。此排序算法虽然代码极短，但效率不高。\
动图：
如果看不了来这里
代码：
template<typename T>
void GnomeSort(T *a,T n)
{
int i=0;
while (i<n)
{
if (i==0||a[i-1]<=a[i]) i++;
else swap(a[i],a[i-1]),i--;
}
}
emm也是\(\mathcal{O}(n^2)\)
5.[冒泡排序逆优化]臭皮匠排序
臭皮匠排序（Stooge Sort），是一种低效的排序算法，在《算法导论》第二版第7章的思考题中被提到，是由Howard Fine等教授提出的所谓“漂亮的”排序算法。将数列平分为三个子串，依次递归排序前两个子串、后两个子串、前两个子串，最后确保整个数列有序。此算法在最坏情况下的递归式为\(T(n) = 3T(2n/3) + 1\)。由主定理很容易知道它的算法复杂性为：\(T(n) = \mathcal{O}(n^{\log_\frac{3}{2}, 3})\)。很显然\(\log_\frac{3}{2}, 3>2\)，也就是说这个算法比插入排序的\(\mathcal{O}(n^2)\)性能还差。
最大就\(\mathcal{O}(n^{2.7})\)吧。。
动图：
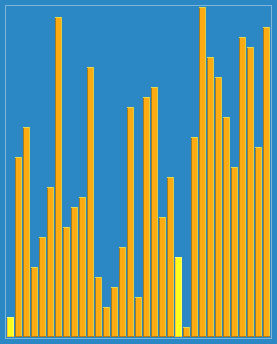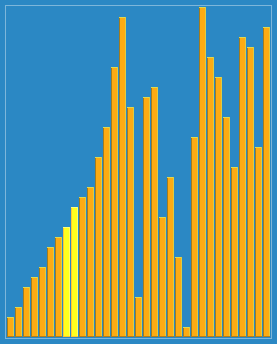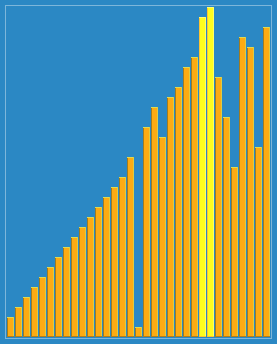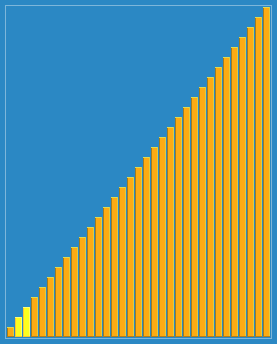
代码如下：
void StoogeSort(int *a,int i,int j)
{
if (a[i]>a[j]) swap(a[i],a[j]);
if ((i+1)>=j) return ;
int k=(j-i+1)/3;
StoogeSort(a,i,j-k);
StoogeSort(a,i+k,j);
StoogeSort(a,i,j-k);
}
6.[冒泡排序优化]奇偶排序
你有没有想冒泡排序优化怎么这么多
奇偶排序（OddEven Sort），是一种相对简单的排序算法，最初发明用于有本地互联的并行计算。此算法通过比较数组中相邻的（奇-偶）位置数字对，如果该奇偶对是错误的顺序（第一个大于第二个），则交换。下一步重复该操作，但针对所有的（偶-奇）位置数字对。如此交替下去，直到不发生交换，则排序结束。
在并行计算排序中，使用该算法，每个处理器对应处理一个值，并仅有与左右邻居的本地互连。所有处理器可同时与邻居进行比较、交换操作，交替以奇-偶、偶-奇的顺序。该算法由Habermann在\(1972\)年最初发表并展现了在并行处理上的效率。但在单处理器串行运行此算法，类似冒泡排序，较为简单但效率并不特别高。
示意图：
最差\(\mathcal{O}(n^2)\)
代码：
void OddEvenSort(int *a, int len)
{
bool swapped=true;
while (swapped)
{
swapped=false;
for (int i=0;i<len-1;i=i+2)
if (a[i]>a[i+1])
{
swap(a[i],a[i+1]);
swapped=true;
}
for (int i=1;i<len-1;i=i+2)
if (a[i]>a[i+1])
{
swap(a[i],a[i+1]);
swapped=true;
}
}
}
冒泡排序优化当然都是稳定排序啦。
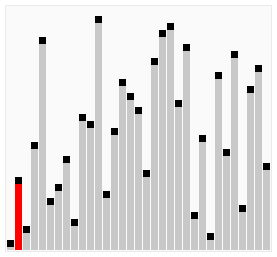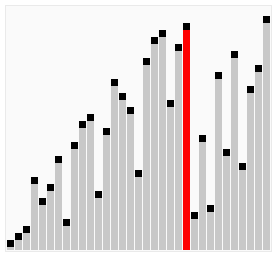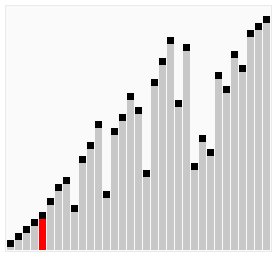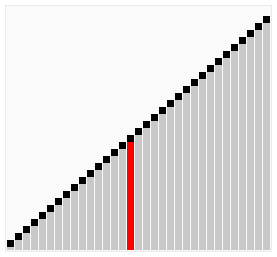
7.选择排序
每次选出一个最小的放到左边，然后依次这么做就行。
时间复杂度\(\mathcal{O}(n^2)\)
动图：
效果图（可视化感觉更强）：
选择排序的在各种初始条件下的排序效果如下：
代码如下：
template<typename T>
void ssort(T* array,int size)
{
for(int i=0;i<size;i++)
{
T Min=array[i];
int k=i;
for (int j=i+1;j<size;j++)
if (array[j]<Min) min=array[j],k=j;
if (k!=i) array[k]=array[i],array[i]=Min;
}
}
你也可以一次确定一个\(\max\)和一个\(\min\),代码不难的。
8.[选择排序优化]堆排序
每次取最小值用堆实现，这样就更快了，可以达到\(\mathcal{O}(n\log n)\)
动图：
代码：
//STL大法好！
template<typename T>
void heapsort(T* a,int n);
{
priority_queue<T> Q;
for (int i=0;i<n;i++) Q.push(a[i]);
for (int i=0;i<n;i++)
{
T Top=Q.top();
Q.pop();
a[i]=Top;
}
}
9.插入排序
从左边设一个有序区，每次从右边插入有序区一个元素，最后就能排序。
时间复杂度\(\mathcal{O}(n^2)\)
动图：
效果图（可视化感觉更强）：
插入排序的在各种初始条件下的排序效果如下：
代码如下：
void Insert_Sort(int* arr,int n)
{
for (int i=0;i<n;i++)
for (int j=i;j>0;j--)
if (arr[j]<arr[j-1])
swap(arr[j],arr[j - 1]);
}
10.[插入排序优化]图书馆排序
Library Sort基于折半查找的插入排序，插入时在元素附近空出一定位置，这样推入后移动元素的复杂度由原来的\(O(n)\)下降为平均\(O(1)\)，于是整个算法的复杂度达到\(\mathcal{O}(n\log n)\)。当输入正序或倒序时，插入点都在同一位置，“留空位”的策略失效，这时就出现最坏复杂度\(\mathcal{O}(n^2)\)。
动图：
由于太冷门所以没有动图
代码：
void librarySort(int length,float factor,int elements[])
{
int i,j;
int expandedLen = (int)((1+factor)*length);
int* orderedElem = (int*) malloc(expandedLen*sizeof(int));
int flag = 1<<31;
for(i=0; i<expandedLen; i++)
orderedElem[i] = flag;
int index = 1;
int numOfIntercalatedElem = 1;
orderedElem[0] = elements[0];
while(length>numOfIntercalatedElem)
{
for(j=0; j<numOfIntercalatedElem; j++)
{
int mid;
int low = 0;
int high = 2 * numOfIntercalatedElem - 1;
while(low <= high)
{
mid = (low + high)/2;
int savedMid = mid;
while(orderedElem[mid] == flag)
{
if(mid == high)
{
mid = savedMid - 1;
while(orderedElem[mid] == flag)
mid--;
break;
}
mid++;
}
if(elements[index] > orderedElem[mid])
{
low = mid + 1;
while(orderedElem[low] == flag)
low = low+1;
}
else high = mid - 1;
}
if(orderedElem[high+1] == flag)
orderedElem[high+1] = elements[index];
else
{
int temp = high+1;
while(orderedElem[temp] != flag)
{
temp--;
if(temp < 0)
{
temp = high+1;
break;
}
}
while(orderedElem[temp] !=flag)
{
temp++;
}
while(temp < high)
{
orderedElem[temp] = orderedElem[temp+1];
temp++;
}
while(temp > high+1)
{
orderedElem[temp] = orderedElem[temp-1];
temp--;
}
orderedElem[temp] = elements[index];
}
index++;
if(index == length)
break;
}
numOfIntercalatedElem *=2;
int generatedIndex;
for(j=numOfIntercalatedElem; j>0; j--)
{
if(orderedElem[j] == flag)
continue;
generatedIndex = j*2;
if(generatedIndex >= expandedLen)
{
generatedIndex = expandedLen - 1;
if(orderedElem[generatedIndex] != flag)
break;
}
orderedElem[generatedIndex] = orderedElem[j];
orderedElem[j] = flag;
}
}
for(i=0; i<expandedLen; i++)
printf("%d\n",orderedElem[i]);
}
11.[插入排序优化]希尔排序
第一次把序列\(k_0\)的倍数分组，每组进行插入排序，
第二次把序列\(k_1\)的倍数分组，每组进行插入排序，
\(\dots\)
最终，总会排好序。
\(k_0>k_1>\dots>k_n,k_n=1\)
动图:
希尔排序在不同数据下的效果：
其中，增量序列\(k\)的取值，目前没有找出最好的。
代码：
void ShellSort(int arr[],int length)
{
if (arr==NULL||length<=0) return;
int increment=length;
while (increment>1)
{
increment=increment/3+1;
for (int i=increment;i<length;i++)
{
int temp=arr[i];
if (arr[i]<arr[i-increment])
{
int j;
for (j=i-increment;j>=0&&arr[j]>temp;j=j-increment)
arr[j+increment]=arr[j];
arr[ +increment]=temp;
}
}
}
}
时间复杂度是\(\mathcal{O}(n^{1.7})\)到\(\mathcal{O}(n^2)\)
12.快速排序
每次取一个基准数，把比他小的都放在左边，比他大的都放在右边，然后递归排序左边和右边。
动图：
效果图（非常震撼！）：
快速排序的在各种初始条件下的排序效果如下：
代码如下：
template<typename T>
void qsort(T* a,int left,int right)
{
int i,j,t,temp;
if (left>right) return;
temp=a[left];
i=left;
j=right;
while(i!=j)
{
while (a[j]>=temp&&i<j) j--;
while (a[i]<=temp&&i<j) i++;
if (i<j) t=a[i],a[i]=a[j],a[j]=t,
}
a[left]=a[i];
a[i]=temp;
qsort(left,i-1);
qsort(i+1,right);
}
时间复杂度平均\(\mathcal{O}(n\log n)\)
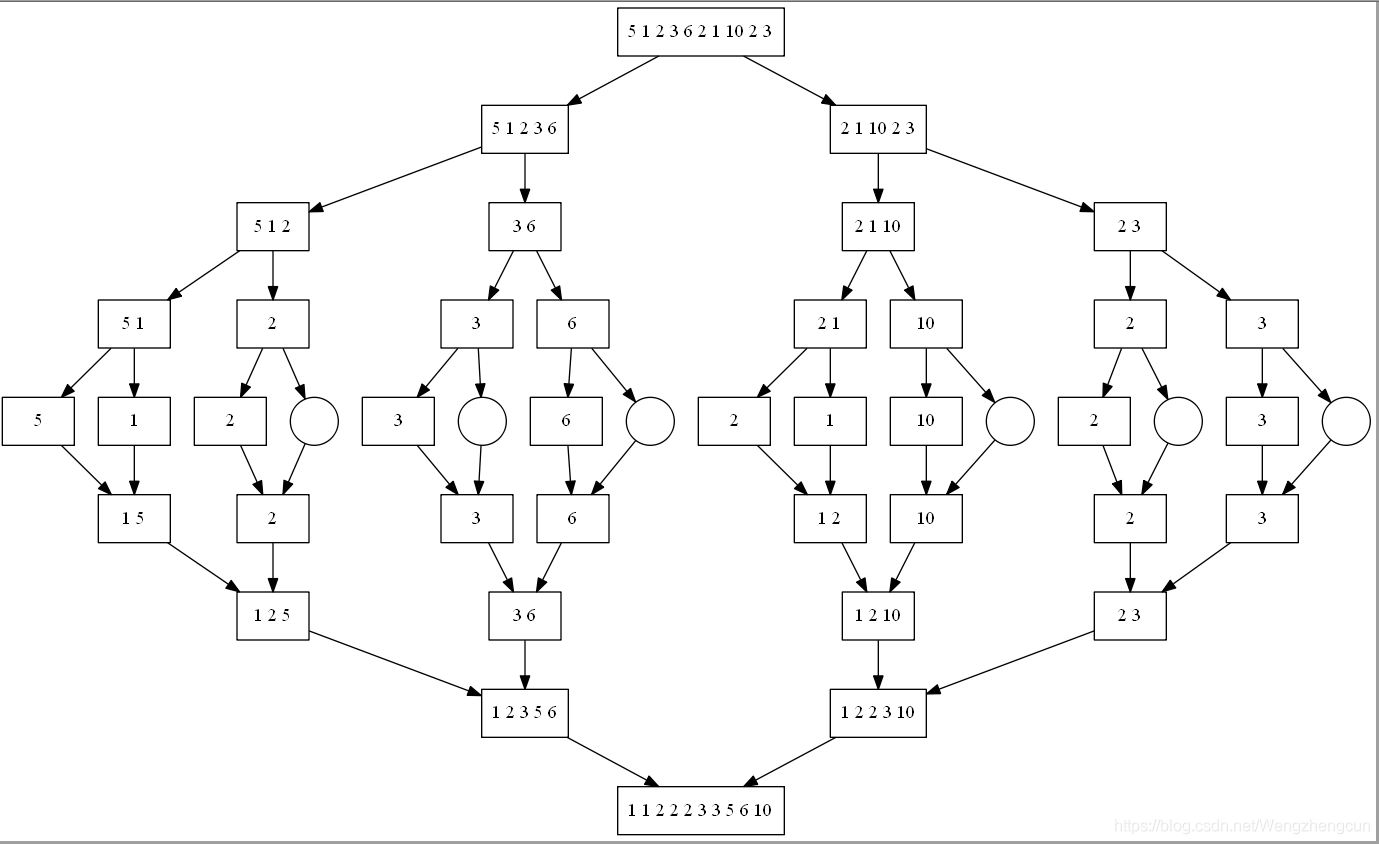
13.归并排序
就是把他分成两半，然后递归左半边和右半边，然后重新合并起来。
图片：
效果图：
归并排序的在各种初始条件下的排序效果如下：
代码：
void Merge(int arr[],int l,int q,int r)
{
int n=r-l+1;
int* tmp=new int[n];
int i=0;
int left=l;
int right=q+1;
while (left<=q&&right<=r)
tmp[i++]=arr[left]<=arr[right]?arr[left++]:arr[right++];
while (left<=q) tmp[i++]=arr[left++];
while (right<=r) tmp[i++]=arr[right++];
for (int j=0;j<n;++j) arr[l+j]=tmp[j];
delete[] tmp;
}
void MergeSort(int arr[],int l,int r)
{
if (l==r) return;
int q=(l+r)/2;
MergeSort(arr,l,q);
MergeSort(arr,q+1,r);
Merge(arr,l,q,r);
}
时间复杂度平均\(\mathcal{O}(n\log n)\)
14.计数排序
用一个数组k，k[i]表示原序列中i出现的次数。
遍历一遍数组就能排序。
动图：
代码很好写，就不写了。
15.[计数排序优化]鸽巢排序
就是把每个数字减去最小值在进行计数排序，节约空间。
代码并不难写，就不写了。
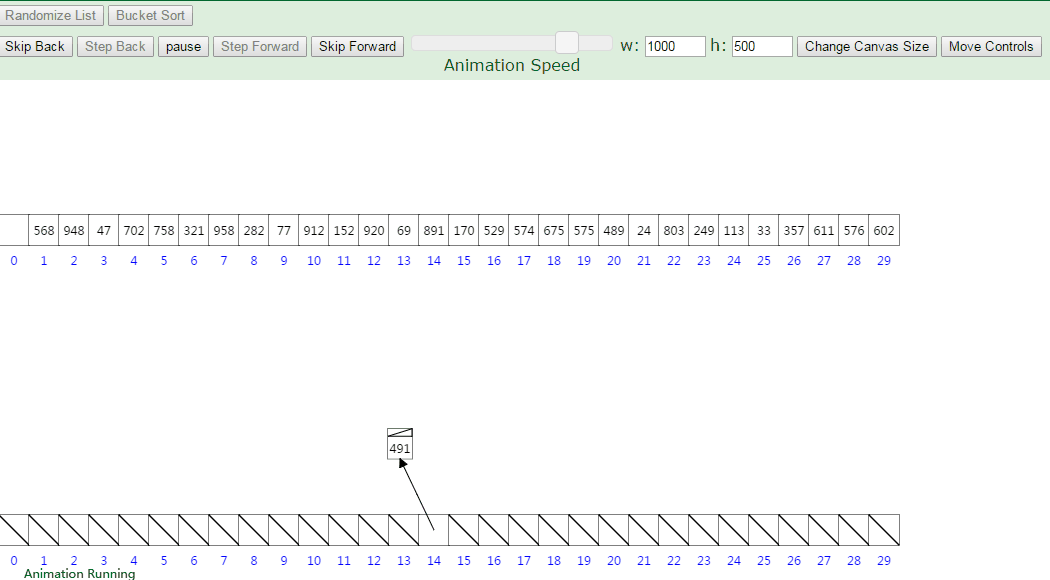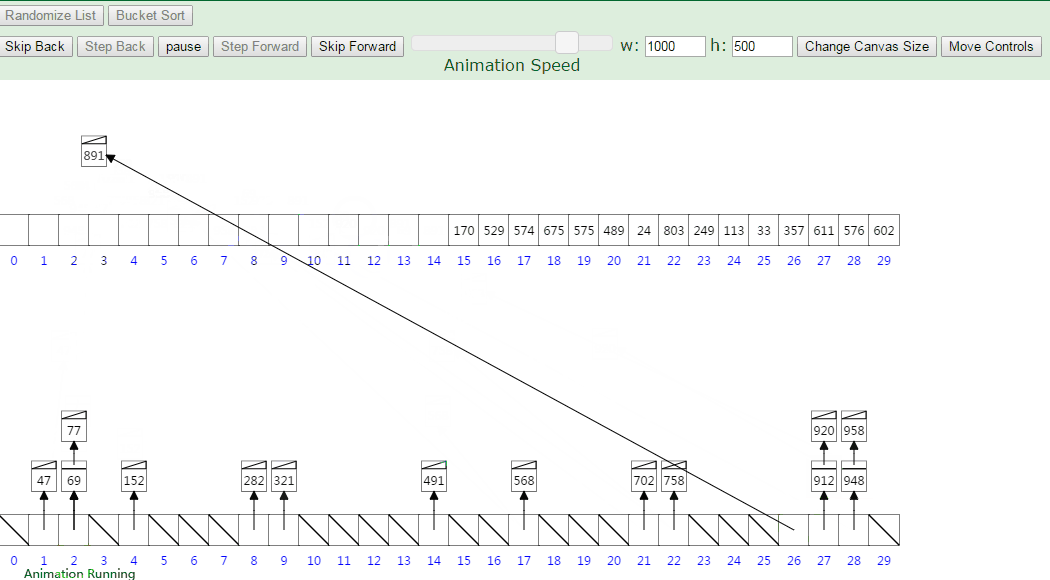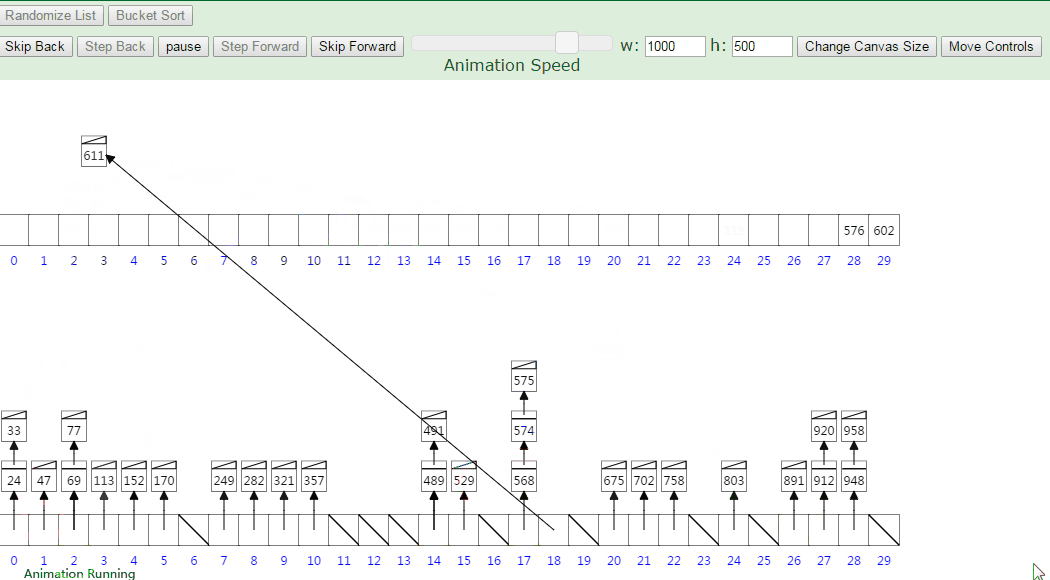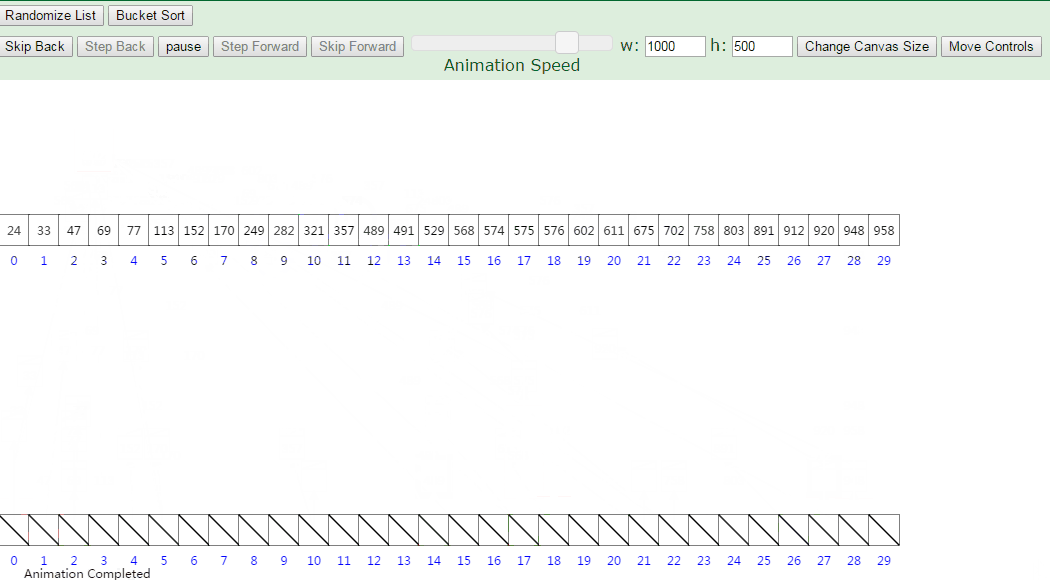
16.桶排序
计数排序不能应对负数和小数，怎么办？
桶排序：开\(n\)个桶，每个桶保存\(i\)到\(j\)之间的数，每次把序列中数字分配到桶中，再将桶内部进行排序，最后输出。
其实可以分配时按照插入排序思路插入的，时间复杂度\(\mathcal{O}(n)\)
代码：
void BucketSort(int *arr, int n)
{
int max = arr[0];
for (int i = 1; i < n; i++)
{
if (arr[i] > max)
max = arr[i];
}
vector<int> *bucket = new vector<int>[max / 10 + 1];
for (int i = 0; i < n; i++)
{
int change = arr[i] / 10;
bucket[change].push_back(arr[i]);
}
for (int i = 0; i < n; i++)
if (bucket[i].size() > 0)
sort(bucket[i].begin(), bucket[i].end());
int index = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j < bucket[i].size(); j++)
arr[index++] = bucket[i][j];
}
17.基数排序
按照数位每次进行多关键字排序，最后就能排好序。
动图：
代码：
bool rxsort(int A[],int l,int h,int d,int k)
{
if (NULL==A||l>h)
return false;
int size = h-l+1;
int* counts = new int[k];
int* temp = new int[size];
int index;
int pval=1;
for (int i=0;i<d;i++)
{
for (int j=0;j<k;j++)
counts[j] = 0;
for (int j=l;j<=h;j++){index = (int)(A[j]/pval)%k;counts[index]++;}
for (int j=1;j<k;j++)
counts[j] = counts[j] + counts[j-1];
for (int j=h;j>=l;j--)
{
index = (int)(A[j]/pval)%k;
temp[counts[index]-1] = A[j];
counts[index]--;
}
for (int j=0;j<size;j++)
A[j+l] = temp[j];
pval = pval*k;
}
delete[] counts;
delete[] temp;
}
时间复杂度\(\mathcal{O}(d(n+k))\)
18.[排序界的一朵奇葩]睡眠排序
睡眠排序的主要逻辑是构造\(n\)个线程，它们和这\(n\)个数一一对应。初始化后，线程们开始睡眠，等到对应的那么多个时间单位后各自醒来，然后输出对应的数。这样最小的数对应的线程最早醒来，这个数最早被输出。等所有线程都醒来，排序就结束了。
由于太奇葩，所有动图和代码都没有
19.[排序界的一朵奇葩]猴子排序
每次随机打乱，直到排好序。
由于太奇葩，所有动图和代码都没有
20.[排序界的一朵奇葩]珠排序
我们知道，在重力的作用下，如果将算盘立起来，无论怎么拨动，算珠最终都会掉下来紧挨在一起，那如果每根柱子上的算珠个数不太一样呢？
见图片:
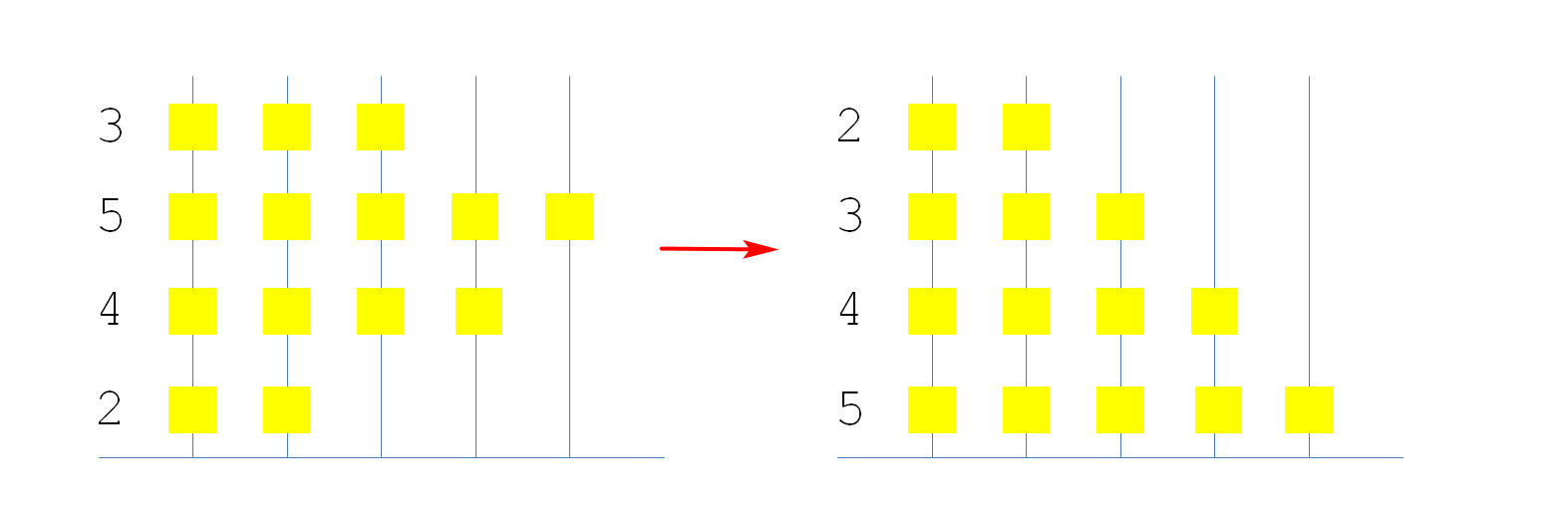
如图，我们看到神奇的重力已经帮我们排好序了。。。。
这个排序算法是时间复杂度最低的！\(\mathcal{O}(1)\)！！！
由于太奇葩，所有动图和代码都没有
21.[排序界的一朵奇葩]面条排序
如果桌子上有一把长短不一的面条，此时你将面条立起来，下端平放在桌面上，此时你用手掌在空中从上往下缓慢移动，慢慢的，你的手掌触碰到了一根面条（这根面条是最高的），你将这根面条抽走（抽走的面条当然想怎么吃就怎么吃），手继续慢慢向下移动，这是，你又碰到了倒数第二高的面条，你又将其抽走\(\dots\)
然后吃到的面条序列就是排序后数组。
由于太奇葩，所有动图和代码都没有
以下是博客签名，正文无关
本文来自博客园，作者：Jijidawang，转载请注明原文链接：https://www.cnblogs.com/CDOI-24374/p/12300350.html
版权声明：本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议（CC BY-NC-SA 4.0）进行许可。看完如果觉得有用请点个赞吧 QwQ
