Magic

3. 栅栏

题面

有俩长度分别为 \(m,n\) 的序列 \(a,b\)，我们有操作

指定一个 \(1\le k\le m\)，先令 \(m\gets m+1\)，并令 \(a_m \gets r\)，\(a_k = a_k \gets r\)，其中 \(r\) 是任意整数

要求在每个时刻都不能有元素 \(\le 0\) .

先进行若干次操作，问有多少对 \((i, j)\) 使得 \(a_i = b_j\)，注意每个 \(i\) 和每个 \(j\) 都互不相同 .

---

\(m\le 50\)，\(n\le 1000\)，序列的元素不超过 \(32767\) .

题解

二分答案，于是问题变为判定取 \(a\) 的前 \(r\) 个元素组成序列 \(a'\) 是否可行.

这可以 dfs 判断，但是会 TLE，优化方法有二：

• 随机化
• 剪枝

我们自然是不喜欢剪枝的，于是随机化哈哈 .

具体说，就是随机那个 \(a\) 序列然后上贪心，跑个 1e5 次就行了（\(m\) 才五十，\(\log m\) 不超过 \(6\)）

这种魔法一般被称作：随机化贪心 .

剪枝做法比较高妙，可以看洛谷 P1528 / P2329 题解（dX！dX！dX！）.

代码（随机）

这里有一个细节：关于高质量的 shuffle .

shuffle 算法已经老生常谈了，这里不再说，但是我们要注意，因为我们是随机 \(10^5\) 次，所以很有可能（存疑）会产生重复，所以我们可以给每个排列都编号，然后对编号 shuffle 一次，就可以确定 dfs 顺序了 .

但是这玩意肯定数组存不下呀，咋办？就要用到俩好几个魔法：

Magic 1. Cantor 展开与其逆

神明 yummy 写过一篇洛谷日报是写这个的 Link（变进制？？？）

Part 1. 康托展开

就是康托展开啦，用于求一个排列的排名（即字典序）

我们知道啊，对于一个排列 \(p_1,p_2,\cdots,p_n\)，比它的字典序小的排列个数就是

\[\sum_{i=1}^n(n-i)!\sum_{j=i}^n[a_j < a_i]\tag{1} \]

为什么呢？略

其实和生成下一个排列思想差不多，就是改成计数了

阶乘肯定是要预处理的， 然后 \(\sum\limits_{j=i}^n[a_j < a_i]\) 这个玩意可以数据结构优化（e.g. 树状数组，平衡树）

于是复杂度瞬间变成 \(O(n\log n)\) .

如果不是排列咋办？有一道题叫 Per，可以看看 .

Part 2. 逆康托展开

就是给一个排名，求这个排列 .

现在我们知道 \((1)\) 式了，咋求排列呐？

这时候 yummy 那个变进制的直观性就来了，\((n-i)!\) 是不会变的吧，只有 \([a_j < a_i]\) 可以变 .

这时候我们要做的工作就是：对于每个数位 \(a_i\)，求出 \(pos\) 使得 \(pos\) 前面的 \([a_j < a_i]\) 中恰好有 \(a_i\) 个 \(0\) .

这玩意要是大力二分就是 \(\log^2\) 的了，我们自然不希望这个 .

线段树不可能写的，咋办？其实树状数组也是可以二分的，可以看看一篇 CF 博客：Binary Search Based on Fenwick Tree .

于是复杂度也是 \(O(n\log n)\) 的 .

关于树状数组二分，很多巨佬都给出了看法：

兔子的看法/fad

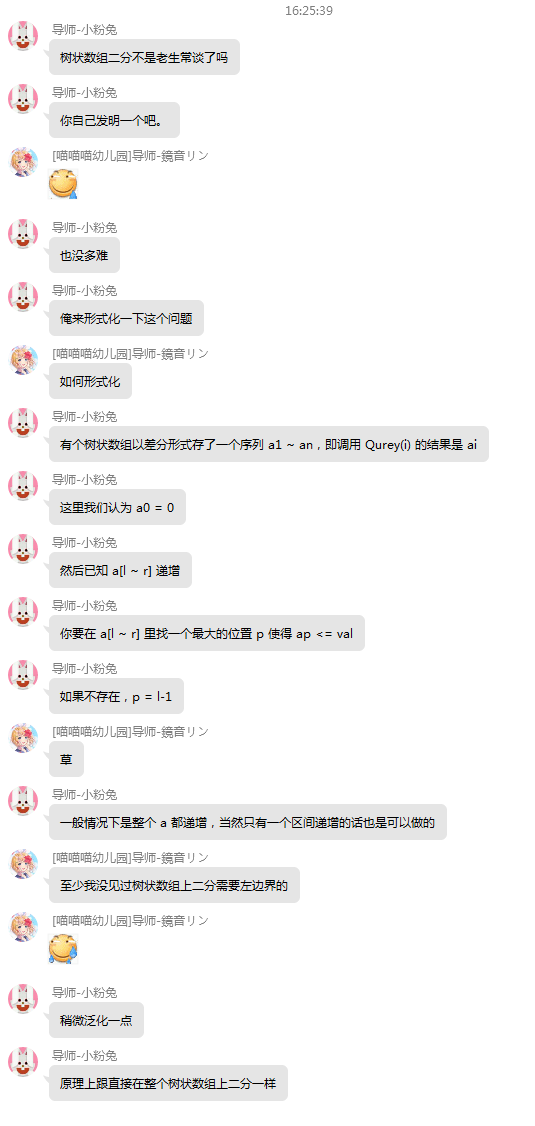
还有 hly 神给出的代码

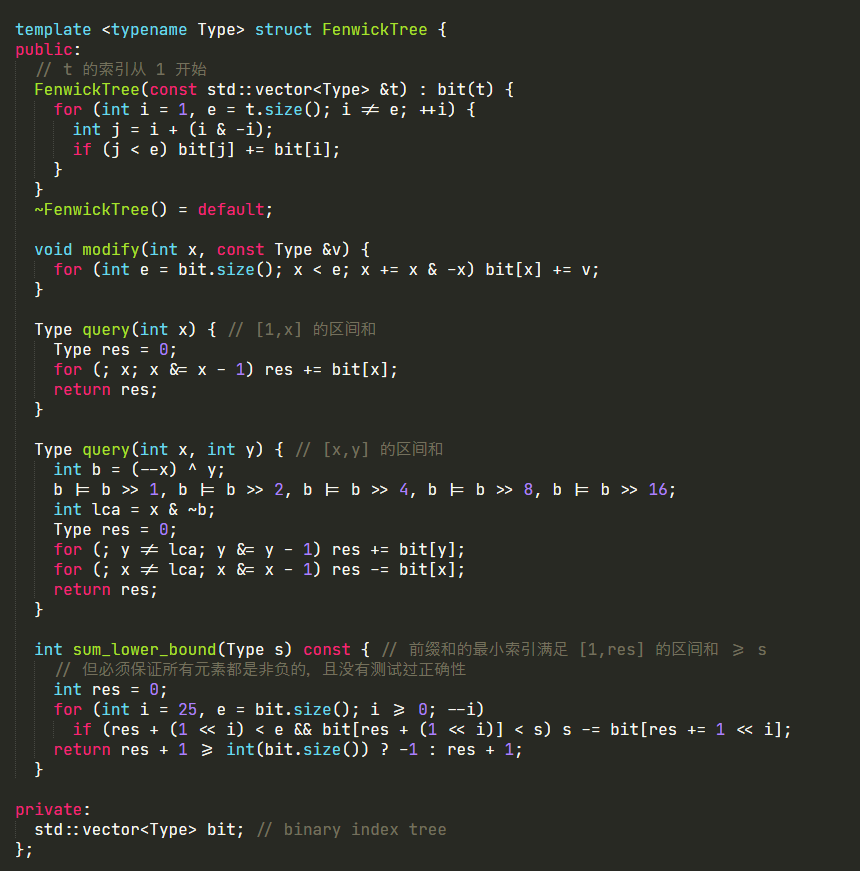
Part 3 代码

线段树版不给了，前面那个 yummy 的博客链接里有 .

Magic 2. \(n\) 里随机选 \(m\)

Question

从 \([1,n]\) 中随机选 \(m\) 个互不相同的数

Algorithm 1（瞎扯）

随机一个 \(1\dots n!\) 的排名，然后康托展开（只用展开前 \(m\) 个）

时间复杂度 \(O(m\log m)\)，空间复杂度 \(O(m)\).

Algorithm 2（正经）

源自 Mivik - 随机的艺术 中的 选择！ 章 . （P.S. 这篇真的非常有用啊，建议多读几遍全文）

懒得写了，自己读吧，时间复杂度 \(O(m)\)，空间复杂度 \(O(m)\) .

代码

但是用这俩魔法虽然随机了，但是复杂度升天，于是就不能跑那么多次随机了，效果没原来好 .

草所以说这么多一点儿用没有是吗？是的

暴力：

代码（贪心）

using namespace std;
typedef long long ll;
const int M = 51, N = 2222;
int n, m, a[M], b[N], c[N], ps[N], sum, now = 0;
bool dfs(int d, int lst) // d 目前数量 
{
	if (d<=0) return true;
	if (now + ps[d] > sum) return false; //
	for (int i = lst; i<=m; i++)
	{
		if (c[i] >= b[d])
		{
			c[i] -= b[d];
			if (a[i] < b[1]) now += c[i];
			if (dfs(d-1, (b[d] == b[d-1]) ? i : 1)) return true;
			if (c[i] < b[1]) now -= c[i];
			c[i] += b[d];
		}
	} return false;
}
bool check(int t){memcpy(c, a, sizeof a); now = 0; return dfs(t, 1);}
int main()
{
	scanf("%d", &m);
	for (int i=1; i<=m; i++) scanf("%d", a + i), sum += a[i];
	scanf("%d", &n);
	for (int i=1; i<=n; i++) scanf("%d", b + i);
	sort(a+1, a+1+m); sort(b+1, b+1+n);
	for (int i=1; i<=n; i++) ps[i] = ps[i-1] + b[i];
	while (ps[n] > sum) --n;
	int l = 0, r = n, ans = 0;
	while (l <= r)
	{
		int mid = (l + r) >> 1;
		if (check(mid)){l = mid + 1; ans = max(ans, mid);}
		else r = mid - 1;
	} printf("%d\n", ans); 
	return 0;
}