Tree *Delete(Tree *T,int n)
{
//将树中指定节点删除的函数
Tree *tmp;
if(T==NULL)
return NULL;
if(T->element==n)
{
if(T->right==NULL) //如果没有右子树,即只有一个该节点儿子左子树
{ //则直接删除
tmp=T;
T=T->left; //用左子树节点代替父节点
free(tmp);
}
else //如果右子树存在
{
tmp=T->right;
while(tmp->left!=NULL)
tmp=tmp->left; //找到右子树的值最小的节点
T->element=tmp->element; //用该节点的值代替原来的节点的值
T->right=Delete(T->right,tmp->element); //递归的删除右子树中用来代替源节点值的节点
T->height = MAX(Height(T->left),Height(T->right)) + 1;
}
return T;
}
if(n < T->element)
T->left = Delete(T->left,n);
else
T->right = Delete(T->right,n);
T->height = MAX(Height(T->left),Height(T->right)) + 1;
return T;
}
下面以实例来解释,假设要删除下图的节点2,
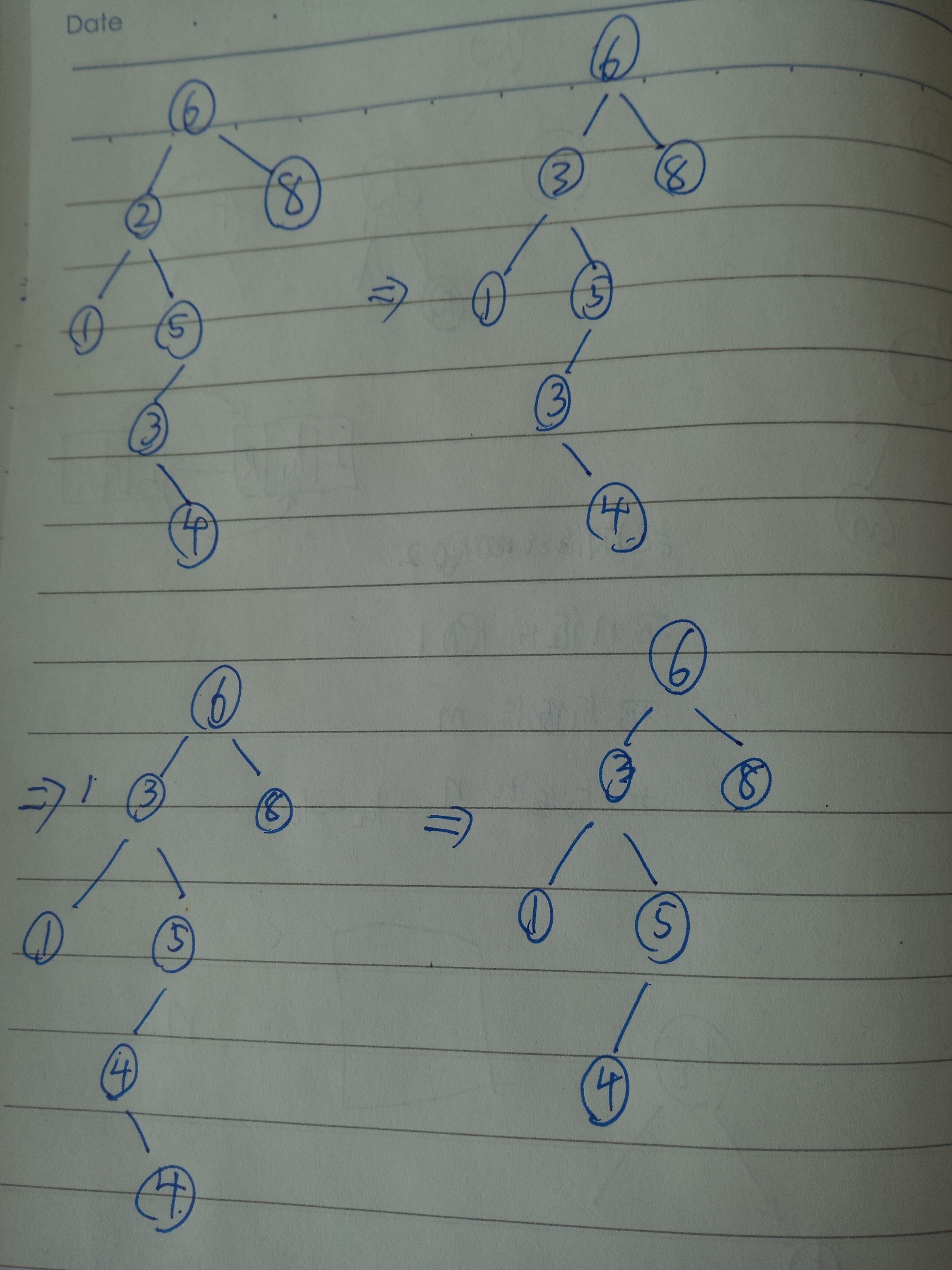
如图,要删除节点2,先看节点2有没有右子树;有右子树,找到其右子树中值最小的节点,于是找到了3;把3的值赋给节点2,现在变成第2附图;下面要递归的删除其右子树中的3节点。
5比3大,所以left递归找到3;3有右子树4,所以要找到3的右子树的值最小的节点。4是其唯一的值,肯定是其最小的节点。于是把4赋给3,变成第3幅图;下面要删除4的右子树中给其赋值的节点4.第一个就是4,好巧,看看其有没有右子树,没有,光杆司令一个;直接删除该节点,把NULL赋给4;于是变成第4幅图。




