二叉树神级遍历算法：morris遍历算法

morris遍历的实质

建立一种机制，对于没有左子树的节点只到达一次，对于有左子树的节点会到达两次

morris遍历的实现原则

记作当前节点为cur。

1. 如果cur无左孩子，cur向右移动（cur=cur.right）
2. 如果cur有左孩子，找到cur左子树上最右的节点，记为mostright
1. 如果mostright的right指针指向空，让其指向cur，cur向左移动（cur=cur.left）
2. 如果mostright的right指针指向cur，让其指向空，cur向右移动（cur=cur.right）

实现以上的原则，即实现了morris遍历。

morris遍历的实质

建立一种机制，对于没有左子树的节点只到达一次，对于有左子树的节点会到达两次

morris遍历的实例

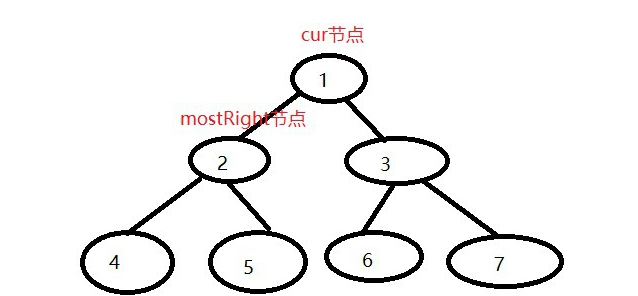
一个树若按层遍历的结构为{1,2,3,4,5,6,7}，即该树为满二叉树，头结点值为1，左右孩子为2,3，叶节点为4,5,6,7

一开始图示：

 

  

我们按照morris遍历来遍历该树。

1）首先cur来到头结点1，按照morris原则的第二条第一点，它存在左孩子，cur左子树上最右的节点为5，它的right指针指向空，所以让其指向1，cur向左移动到2。

2）2有左孩子，且它左子树最右的节点4指向空，按照morris原则的第二条第一点,让4的right指针指向2，cur向左移动到4

3）4不存在左孩子，按照morris原则的第一条，cur向右移动，在第二步中，4的right指针已经指向了2，所以cur会回到2

4）重新回到2，有左孩子，它左子树最右的节点为4，但是在第二步中，4的right指针已经指向了2，不为空。所以按照morris原则的第二条第二点，2向右移动到5，同时4的right指针重新指向空

5）5不存在左孩子，按照morris原则的第一条，cur向右移动，在第一步中，5的right指针已经指向了1，所以cur会回到1

6）cur回到1，回到头结点，左子树遍历完成，1有左孩子，左子树上最右的节点为5，它的right指针指向1，按照morris原则的第二条第二点，1向右移动到3，同时5的right指针重新指回空

……

当到达最后一个节点7时，按照流程下来，此时7无左右孩子，遍历结束。

 

 

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        TreeNode predecessor = null;

        while (root != null) {
            if (root.left != null) {
                // predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止
                predecessor = root.left;
                while (predecessor.right != null && predecessor.right != root) {
                    predecessor = predecessor.right;
                }
                
                // 让 predecessor 的右指针指向 root，继续遍历左子树
                if (predecessor.right == null) {
                    predecessor.right = root;
                    root = root.left;
                }
                // 说明左子树已经访问完了，我们需要断开链接
                else {
                    res.add(root.val);
                    predecessor.right = null;
                    root = root.right;
                }
            }
            // 如果没有左孩子，则直接访问右孩子
            else {
                res.add(root.val);
                root = root.right;
            }
        }
        return res;
    }
}