「题解」CF311E Biologist
【题解】CF311E Biologist
非常好的一道最小割。
思路
首先看到每一个位置又会有 \(0 1\) 两种情况，然后要满足一些要求，求最大收益，考虑类似于 P4313 文理分科 和 P1361 小M的作物 这种集合划分的建图方法，也就是要用最小割求解。
由于我们要求的是最大收益，所以我们要先明确要最小化什么，然后用 所有可能获得的收益 减去 最小割 就是 最大收益。
根据题意，我们首先希望反转某个位置的代价尽可能小，同时被割去的收益和朋友的赔礼也应该尽可能小，也就是要最小化 反转的代价 不能选的要求 和 朋友的赔礼。
每一个位置有 \(0 1\) 两种情况，考虑将所有一开始为 \(1\) 的点放在左边 ( \(1\) 集合)，为 \(0\) 的点放在右边 ( \(0\) 集合)，分别于 \(S,T\) 连容量为 \(v_i\) 的边。
其中，割掉 \(1\) 集合中的点 与 \(S\) 相连的边则表示这个点属于 \(0\) 这个集合，同样，割掉 \(0\) 集合中的点 与 \(T\) 相连的边则表示这个点属于 \(1\) 集合。
反转某个位置的代价考虑完了，现在开始解决那些要求。
先考虑 要求每个位置都为 \(1\) 的要求。
现在考虑这样一种情况。
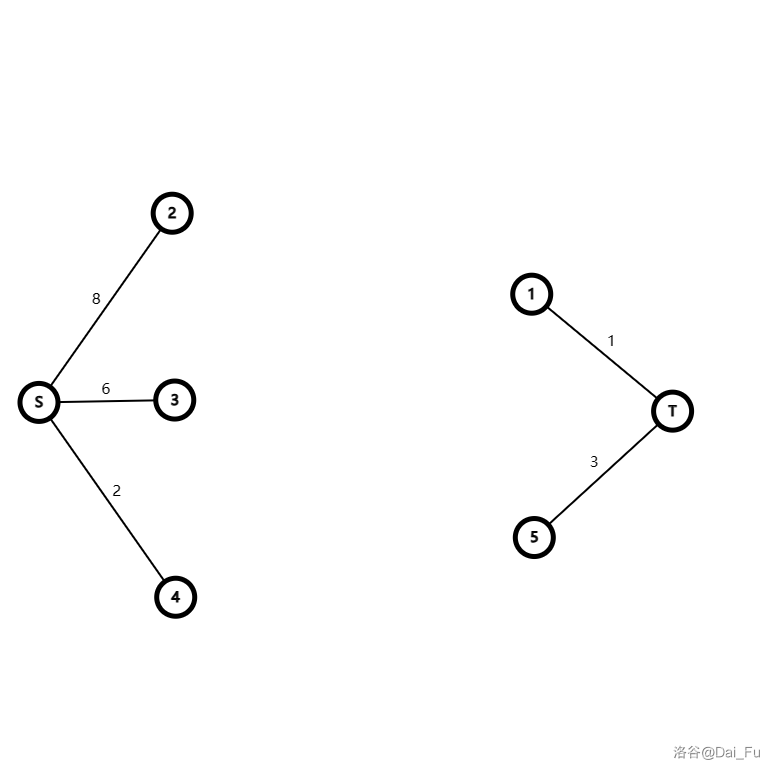
其中 2 3 4 属于 \(1\) 集合， 1 5 属于 \(0\) 集合。 同时我们要求 2 3 都为 \(1\) 可以获得 \(w_i\) 的收益。
考虑这么建图：
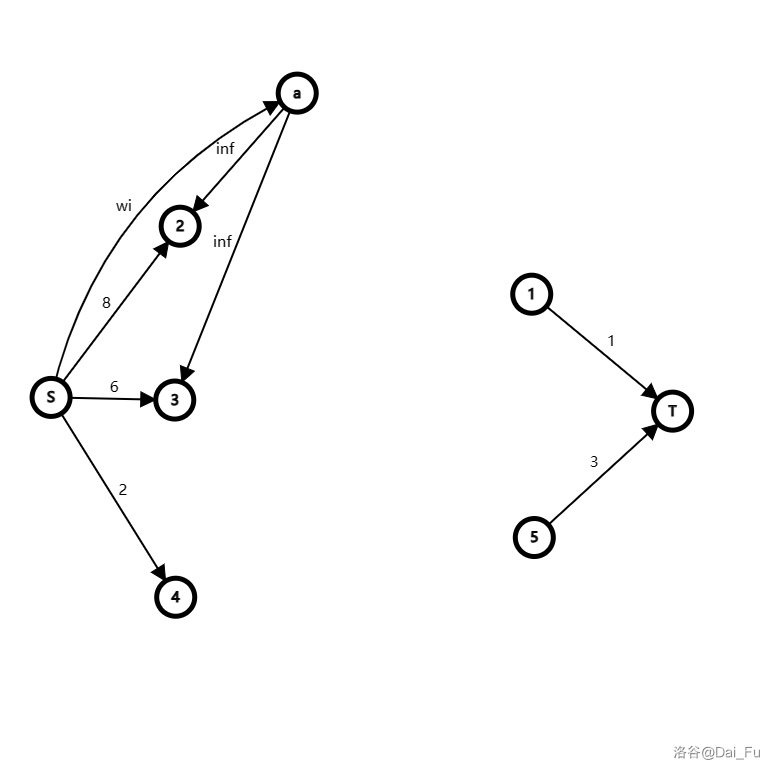
如果 2 3 都为 \(1\) ,则不会割去任何边。如果 2 3 有一个不为 \(1\) ，则会割去 \(w_i\) 和那些点反转的边，满足题意。
现在我们要求 1 4 5 都为 \(0\) 可以获得 \(w_i\) 收益。
也就是这种情况：
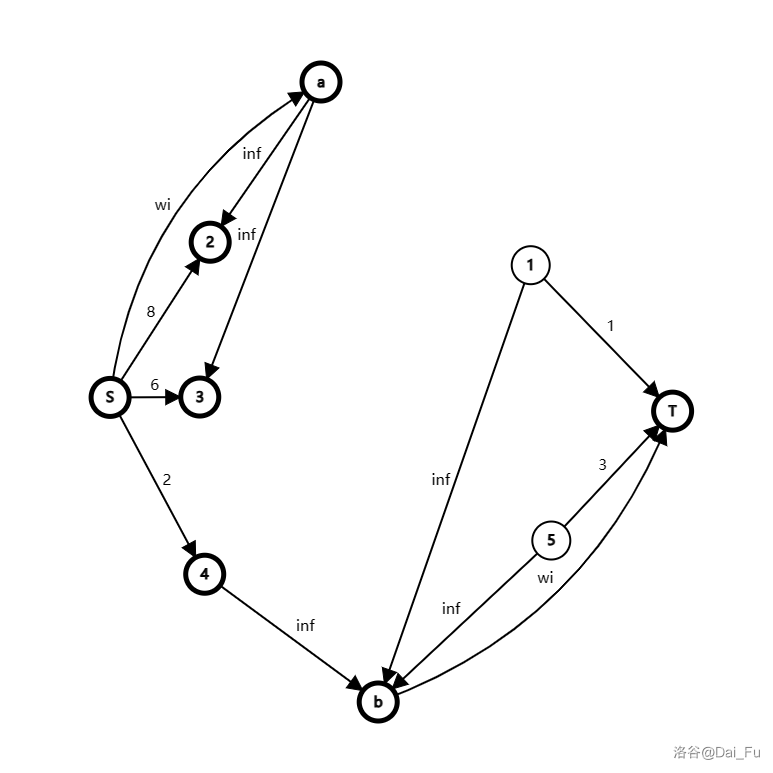
同样的，因为我们不能割去 \(inf\) 的边，所以，如果我们不想割掉这个要求，就必须让 4 属于 \(0\) 集合，也就是得割去 \(2\) 那条边，否则就必须割去 \(w_i\) 。
现在只剩下朋友的要求没有解决了。
很简单，如果某个要求是朋友提出的，只需要在 \(w_i\) 上加上 \(g\) 。
分析这样做的正确性：我们的答案为 \(\sum\limits_{i=1}^m{w_i}-最小割\) ，再加上朋友的要求之后，如果某个要求被割掉了，答案同样也会减去 \(g\) ，满足题意。
综上所述：
S -> 一开始为1的点 连容量为 vi 的边。
一开始为0的点 -> T 连容量为 vi 的边。
对于每个要求：
新建一个点a。
如果要求每个数字为1：
S -> a 容量为 wi (+pi)
a -> 所以要求的点 容量为 inf 的边
如果要求每个数字为0：
b -> T 容量为 wi (+pi)
所以要求的点 -> b 容量为 inf 的边
最后答案为 \(\sum\limits_{i=1}^m{w_i}-最小割\) 。
代码
#include<bits/stdc++.h>
using namespace std;
const int MX_N=50100,MX_M=500100;
const int INF=0x3f3f3f3f;
struct node{
int to,next,w;
}edge[MX_M<<1];
int head[MX_N]={0},edge_cnt=0;
inline void Add(int x,int y,int w){
node &i=edge[edge_cnt];
i.w=w,i.to=y,i.next=head[x];
head[x]=edge_cnt++;
}
inline void add(int x,int y,int w){
Add(x,y,w),Add(y,x,0);
}
int s=0,t=MX_N-1;
int cur[MX_N]={0},dist[MX_N]={0};
bool bfs(){
for(int i=0;i<MX_N;i++) cur[i]=head[i],dist[i]=-1;
queue<int > qu;qu.push(s);dist[s]=0;
while(!qu.empty()){
int now=qu.front();qu.pop();
for(int i=head[now];i!=-1;i=edge[i].next){
int to=edge[i].to;
if(dist[to]==-1&&edge[i].w){
dist[to]=dist[now]+1;
qu.push(to);
}
}
}
return dist[t]!=-1;
}
int dfs(int now,int flow){
if(now==t) return flow;
int left=flow;
for(int &i=cur[now];i!=-1;i=edge[i].next){
int to=edge[i].to,w=edge[i].w;
if(dist[to]==dist[now]+1&&w){
int cur_flow=dfs(to,min(left,w));
left-=cur_flow;
edge[i].w-=cur_flow;
edge[i^1].w+=cur_flow;
if(left==0) break;
}
}
if(flow==left) dist[now]=-1;
return flow-left;
}
int dinic(){
int sum=0;
while(bfs()){
sum+=dfs(s,INF);
}
return sum;
}
bool st[10100]={0};
signed main(){
memset(head,-1,sizeof(head));
//=======================================================
int n,m,g;scanf("%d%d%d",&n,&m,&g);
for(int i=1;i<=n;i++) scanf("%d",&st[i]);
for(int i=1;i<=n;i++){
int vi;scanf("%d",&vi);
if(st[i]){
add(s,i,vi);
}
else{
add(i,t,vi);
}
}
int sum=0;
for(int i=1;i<=m;i++){
int op,wi,ki;scanf("%d%d%d",&op,&wi,&ki);sum+=wi;
for(int j=1;j<=ki;j++){
int xi;scanf("%d",&xi);
if(op) add(i+n,xi,INF);
else add(xi,i+n,INF);
}
int fri;scanf("%d",&fri);
if(op){
add(s,i+n,wi+fri*g);
}
else{
add(i+n,t,wi+fri*g);
}
}
printf("%d",sum-dinic());
//=======================================================
return 0;
}//CF311E
求过，求关注。
