1.1.3.2 最小割之最大权闭合图、最大密度子图

1.1.3.2 最小割之最大权闭合图、最大密度子图

最大权闭合图

概述

一个有向图的闭合图是指：该有向图的一个点集，且该点集的所有出边都指向该点集。

最大权闭合图即是其中点权和最大的闭合图。

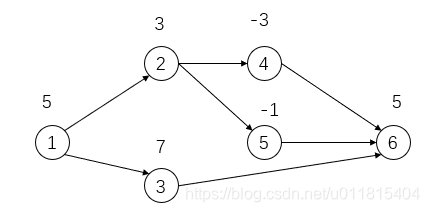
如上图，能选的子图有：1,2,3,4,5,6, 3,6、2,4,5,6、4,6、5,6、6 ，他们的权值分别为：\(0\)、\(16\)、\(12\)、\(4\)、\(2\)、\(4\)、\(5\)

因此最大闭合子图为：1,2,3,4,5,6，权值为 \(16\)

解法

最大权闭合子图可以转为最小割问题来求解。

首先记录整个图中所有正点权之和，然后建立相应的流量网络

设一个超级源点 \(S\) 与一个超级汇点 \(T\)，从源点 \(S\) 向每个正权点连一条容量为权值的边，每个负权点向汇点 \(T\) 连一条容量为权值的绝对值的边，原图中的边容量均设为 INF

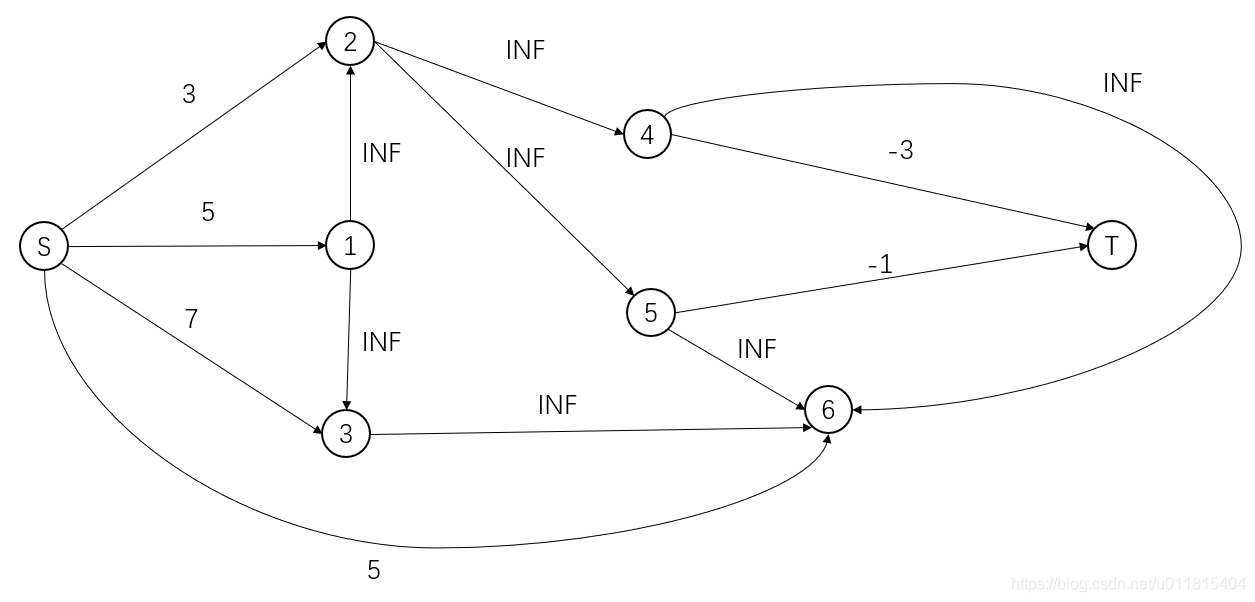
由于原图的边都是无穷大的，那么割边一定是与源点 \(S\) 或汇点 \(T\) 相连的，那么就有以下的含义：

割掉 S 与 i 的边，表示不选择 i 点作为子图的点
割掉 i 与 T 的边，表示选择 i 点为子图的点
如果 S 与 i 有边，表示 i 存在子图中
如果 i 与 T 有边，表示 i 不存在于子图中

在建完图后，利用 \(Dinic\) 求最小割，割掉后与源点 \(S\) 连通的点就构成了最大权闭合子图，最小割的值是不选的正权之和与要选的负权绝对值之和。

那么最大权闭合子图的权值就是：\(正权值之和-最小割\)

证明

定义简单割

割边只存在与源点或与汇点相连的边。

证明上面建图最小割为简单割

所有与源或汇关联的边组成的割集容量是有限的，为所有点权的绝对值和，最小割容量也至多为该绝对值和。故最小割不可能取任何容量为正无穷的边，即最小割为简单割。

证明网络的简单割与原图闭合图一一对应

1. 闭合图对应简单割。假设闭合图对应的不是简单割，那么一定存在一条正无穷的边连接两个点集与闭合图前提矛盾。所有原假设成立。

2. 简单割对应闭合图。由于是简单割，所以最小割与源点相连的点集的出边一定在自己原来所在点集内。

所以命题成立。

最优性

\(最小割=(不选的正权之和+要选的负权绝对值之和)\)

\(最大权闭合子图=(正权之和-不选的正权之和-要选的负权绝对值之和)=正权值和-最小割\)

因为正权值和，是定值，而最小割保证值最小，所以最大权闭合子图一定最优。

Tip

最大权闭合图建模往往伴随有“必须”等限制。

最大密度子图

鸽