[题解] [TJOI2013]攻击装置

前言

没啥好说的，题目链接。

题目简述

\(n\) 行 \(n\) 列的矩阵中，若该点为 \(0\) ，则可以安放装置 \((x,y)\) ，若装置会攻击\((x-1,y-2)\) ， \((x-2,y-1)\) ， \((x+1,y-2)\) ， \((x+2,y-1)\) ， \((x-1,y+2)\) ， \((x-2,y+1)\) ， \((x+1,y+2)\) ， \((x+2,y+1)\) 这八个位置的装置。求最多可以放多少装置。

思路

最开始时，没啥思路，将一个装置在一张图中表示出来，攻击范围如下：

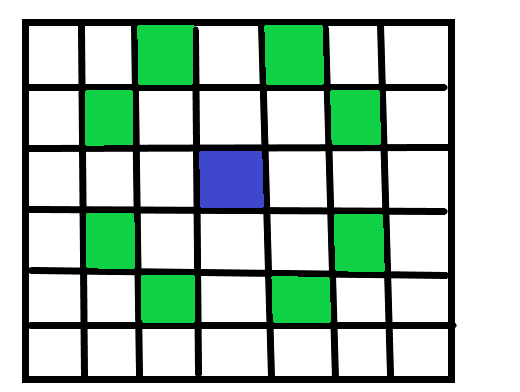
绿色点为蓝色点能够攻击到的点。可以发现很像国际象棋的棋盘，进一步做如下染色：

这样对比两张图，可以发现，白色点可以能够攻击到的点全都是黑色点，黑色点可以能够攻击到的点全都是白色点。白色点与白色点、黑色点与黑色点之间不会有联系。

这样的两个同一集合内的点互不关联，且有两个集合的问题不难转换成二分图来求解。其中，不妨设白色点为左部点，黑色点为右部点，构建一张二分图。

求解的问题是最大的互不攻击的装置，即可以转换为二分图的最大独立集问题。而最大独立集的点数等于二分图中所有点的个数减去最大匹配的边数，进而用网络最大流来求解。

C++代码

#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
using namespace std;
#define INF 0x3f3f3f3f
#define Min(a, b) ((a) < (b) ? (a) : (b))
void Quick_Read(int &N) {
	N = 0;
	int op = 1;
	char c = getchar();
	while(c < '0' || c > '9') {
		if(c == '-')
			op = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9') {
		N = (N << 1) + (N << 3) + (c ^ 48);
		c = getchar();
	}
	N *= op;
}
void Read_OneNumber(int &N) {
	N = 0;
	char c = getchar();
	while(c < '0' || c > '9')
		c = getchar();
	N = c ^ 48;
}
const int MAXN = 2e2 + 5;
const int MAXM = 4e4 + 5;
const int MAXK = 10;
int color[MAXN][MAXN];
int addx[MAXK] = {0, -1, -2, 1, 2, -1, -2, 1, 2};
int addy[MAXK] = {0, -2, -1, -2, -1, 2, 1, 2, 1};
int n, Sum;
struct Node {
	int to, val, rev;
	Node() {}
	Node(int T, int V, int R) {
		to = T;
		val = V;
		rev = R; 
	} 
};
vector<Node> v[MAXM];
queue<int> q;
int be[MAXM], de[MAXM];
int s, t;
bool Bfs_Dinic() {//将残量网络分层
	while(!q.empty())
		q.pop();
	memset(de, 0, sizeof(de));
	q.push(s);
	de[s] = 1;
	be[s] = 0;
	while(!q.empty()) {
		int now = q.front(); q.pop();
		int SIZ = v[now].size();
		for(int i = 0; i < SIZ; i++) {
			int next = v[now][i].to;
			if(!de[next] && v[now][i].val) {
				be[next] = 0;
				de[next] = de[now] + 1;
				q.push(next);
				if(next == t)
					return true;
			}
		}
	}
	return false;//找不到增广路
}
int Dfs_Dinic(int now, int flow) {//在残量网络中寻找增广路并增广
	if(now == t || !flow)
		return flow;
	int surp = flow;
	int SIZ = v[now].size();
	for(int i = be[now]; i < SIZ && surp; i++) {
		be[now] = i;//弧优化
		int next = v[now][i].to;
		if(v[now][i].val && de[next] == de[now] + 1) {
			int maxnow = Dfs_Dinic(next, Min(surp, v[now][i].val));
			if(!maxnow)
				de[next] = -1;
			v[now][i].val -= maxnow;
			v[next][v[now][i].rev].val += maxnow;
			surp -= maxnow;
		}
	}
	return flow - surp;
}
int Dinic() {//最大流
	int res = 0, flow;
	while(Bfs_Dinic())
		while(flow = Dfs_Dinic(s, INF))
			res += flow;
	return res;
}
int Serial_Number(int i, int j) {//求该点的边号，勉强算个hash
	return (i - 1) * n + j;
}
void Read() {
	Quick_Read(n);
	s = 0; t = n * n + 1;
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= n; j++) {
			Read_OneNumber(color[i][j]);
			Sum += !color[i][j];
		}
	for(int i = 1; i <= n; i++)//构建二分图
		for(int j = 1; j <= n; j++) {
			if(color[i][j] || !((i + j) & 1))
				continue;
			int now = Serial_Number(i, j);
			for(int k = 1; k <= 8; k++) {
				if(i + addx[k] < 1 || i + addx[k] > n || j + addy[k] < 1 || j + addy[k] > n)
					continue;
				int next = Serial_Number(i + addx[k], j + addy[k]);
				if(color[i][j])
					continue;
				int id1 = v[now].size();
				int id2 = v[next].size();
				v[now].push_back(Node(next, 1, id2));
				v[next].push_back(Node(now, 0, id1));
			}
		}
	for(int i = 1; i <= n; i++)//构建网络
		for(int j = 1; j <= n; j++) {
			if(color[i][j])
				continue;
			int now = Serial_Number(i, j);
			int idn = v[now].size();
			if((i + j) & 1) {
				int ids = v[s].size();
				v[s].push_back(Node(now, 1, idn));
				v[now].push_back(Node(s, 0, ids));
			}
			else {
				int idt = v[t].size();
				v[now].push_back(Node(t, 1, idt));
				v[t].push_back(Node(now, 0, idn));
			}
		}
}
void Write() {
	printf("%d", Sum - Dinic());//二分图最大独立集
}
int main() {
	Read();
	Write();
	return 0;
}