[冲刺国赛2022] 模拟赛15

数列

题目描述

你得到了一个长度为 $n$ 的数列 $a$ ，每个元素为 $[1,m]$ 中的整数，可以生成 $b_i=\max\{j|j<i\and a_j>a_i\}$

现在给你数列 $b$ ，其中有一些位置被损坏了（值为 $-1$ ），请求出有多少满足条件的 $a$

$n\leq 100,m\leq 10^5$

解法

可以根据 $b$ 写出一个表示大小关系，每条边代表或者 $\leq$ 的符号。

考虑根据 $\tt DAG$ 构造出一棵内向树，使得内向树可以表示同样的大小关系，构造方法如下：

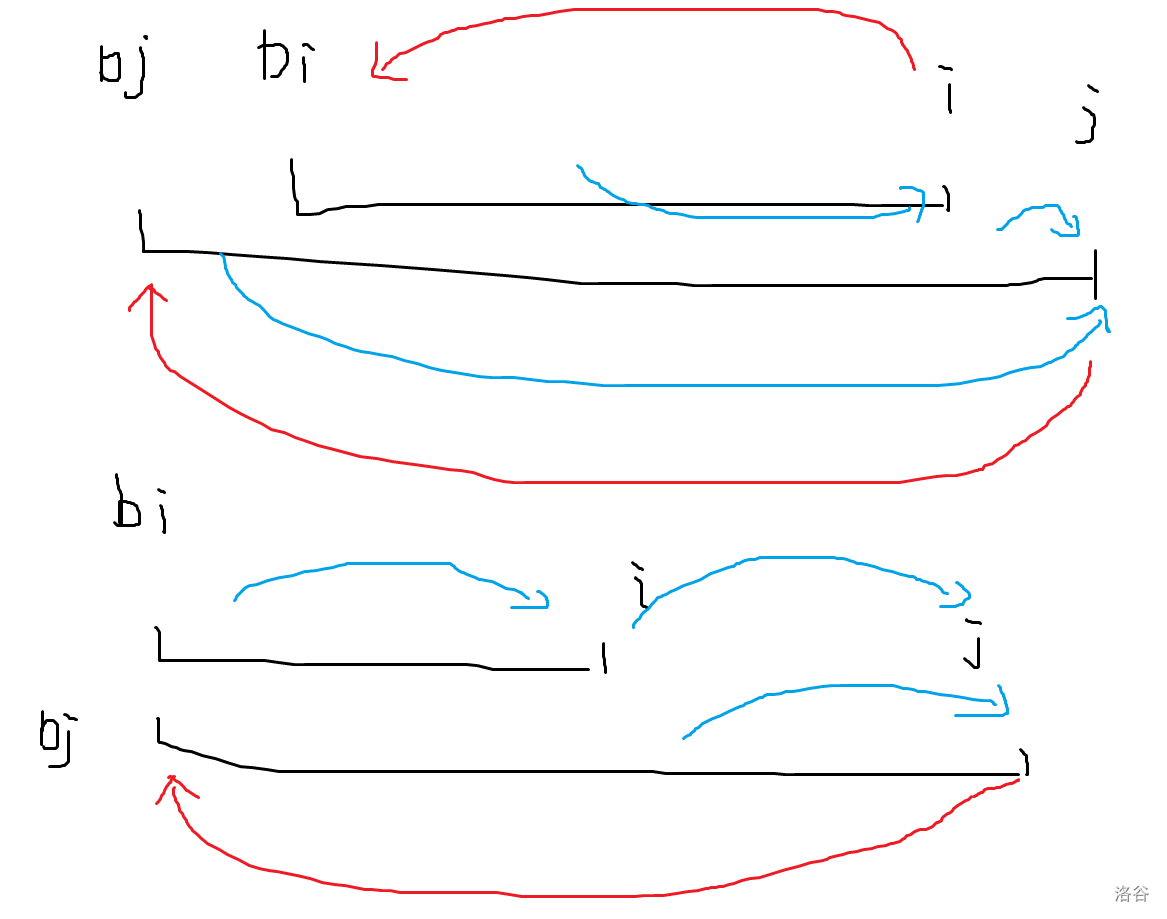
由于出现区间相交即无解，所以我们只需要考虑包含时怎么做。上半部分展示了左端点不重叠时的构造方法，下半部分展示了左端点重叠时的构造方法，其中红边代表 $<$ 号，蓝边代表 $\leq$ 号。

构造出内向树以后直接 $dp$ ，设 $dp[i][j]$ 表示要求子树 $i$ 的权值 $\leq j$ 的方案数，时间复杂度 $O(nm)$

#include <bits/stdc++.h>
using namespace std;
const int M = 105;
const int MOD = 998244353;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,b[M],vis[M],tg[M];vector<int> g[M];
int rp[M],fa[M],dp[M][100005];
void dfs(int u)
{
    for(int i=1;i<=m;i++) dp[u][i]=1;
    for(int v:g[u])
    {
        dfs(v);
        for(int j=1;j<=m;j++)
            dp[u][j]=1ll*dp[u][j]*dp[v][j-tg[v]]%MOD;
    }
    for(int i=1;i<=m;i++)
        dp[u][i]=(dp[u][i]+dp[u][i-1])%MOD;
}
signed main()
{
    //freopen("array.in","r",stdin);
    //freopen("array.out","w",stdout);
    n=read();m=read();
    for(int i=1;i<=n;i++)
    {
        b[i]=read();
        if(b[i]<0) continue;
        if(vis[b[i]]) {puts("0");return 0;}
        for(int j=b[i]+1;j<i;j++)
            if(!vis[j]) vis[j]=1,rp[j]=i;
        fa[i]=b[i];tg[i]=1; 
    }
    for(int i=1;i<=n;i++)
    {
        if(rp[i] && b[rp[i]]==fa[i])
            fa[i]=rp[i],tg[i]=0;
        if(fa[i]) g[fa[i]].push_back(i);
    }
    int ans=1;
    for(int i=1;i<=n;i++) if(!fa[i])
        dfs(i),ans=1ll*ans*dp[i][m]%MOD;
    printf("%d\n",ans);
}

子串

题目描述

定义 $cnt(s,t)$ 表示 $t$ 在 $s$ 中的出现次数。对于字符串 $s$ ，定义一个子串 $t$ 是重要的，当且仅当对于任意以 $t$ 为子串的 $t'$ ，都满足 $cnt(s,t')<cnt(s,t)$

给定串 $S$ ，对于 $S$ 的每个前缀求出，把这个前缀当成 $s$ 时，重要串有多少个。

$|S|\leq 10^6$ ，字符集 0~9

解法

考虑判断条件可以转化成：在 $t$ 的前面或者后面加一个字符得到 $t'$ ， $t'$ 的出现次数不能等于 $t$

如果只考虑在前面加入字符，那么答案就是后缀自动机的节点数，可以在构建后缀自动机的时候得到个数。

再考虑在后面加入字符，如果某种节点的转移边只有一种的话，走这条转移边所得的 $t'$ 出现次数会等于 $t$ ，但是有一种情况需要特判：对于存在下一个字符为空的串 $t$ 一定是重要的。

根据上面的描述，可以得到答案为：后缀自动机上节点数减一再减去不在最后一条链上的出度为 $1$ 的节点。

所以我们维护转移边出度为 $1$ 的点数，用 $\tt dfn$ 序和树状数组来维护链，就可以计算答案，时间复杂度 $O(n\log n)$

#include <bits/stdc++.h>
using namespace std;
const int M = 2000005;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,cnt,last,Ind,res,b[M],ans[M];
int dfn[M],siz[M],out[M];char s[M];
vector<int> g[M];vector<pair<int,int>> v[M];
struct node{int ch[10],fa,len;}a[M<<1];
void add(int id,int c)
{
    int p=last,np=last=++cnt;
    a[np].len=a[p].len+1;
    for(;p && !a[p].ch[c];p=a[p].fa)
    {
        a[p].ch[c]=np;out[p]++;
        v[id].push_back(make_pair(p,1));
    }
    if(!p) a[np].fa=1;
    else
    {
        int q=a[p].ch[c];
        if(a[p].len+1==a[q].len) a[np].fa=q;
        else
        {
            int nq=++cnt;a[nq]=a[q];
            a[nq].len=a[p].len+1;out[nq]=out[q];
            v[id].push_back(make_pair(nq,out[nq]));
            a[np].fa=a[q].fa=nq;
            for(;p && a[p].ch[c]==q;p=a[p].fa)
                a[p].ch[c]=nq;
        }
    }
}
void dfs(int u)
{
    dfn[u]=++Ind;siz[u]=1;
    for(int v:g[u])
        dfs(v),siz[u]+=siz[v];
}
//
void ins(int x,int c)
{
    for(int i=x;i<=cnt;i+=i&(-i))
        b[i]+=c;
}
int ask(int x)
{
    int r=0;
    for(int i=x;i>0;i-=i&(-i))
        r+=b[i];
    return r;
}
void Ins(int l,int r,int c)
{
    ins(l,c);ins(r+1,-c);
}
void upd(int x,int y)
{
    if(out[x]==1)
        Ins(dfn[x],dfn[x]+siz[x]-1,-1),res--;
    out[x]+=y;
    if(out[x]==1)
        Ins(dfn[x],dfn[x]+siz[x]-1,1),res++;
}
signed main()
{
    freopen("string.in","r",stdin);
    freopen("string.out","w",stdout);
    n=read();scanf("%s",s+1);
    last=cnt=1;
    for(int i=1;i<=n;i++)
        add(i,s[i]-'0'),ans[i]=cnt-1;
    for(int i=2;i<=cnt;i++)
        g[a[i].fa].push_back(i);
    dfs(1);
    for(int i=1;i<=cnt;i++) out[i]=0;
    for(int i=1,p=1;i<=n;i++)
    {
        p=a[p].ch[s[i]-'0'];
        for(auto x:v[i])
            upd(x.first,x.second);
        ans[i]+=ask(dfn[p])-res;
    }
    for(int i=1;i<=n;i++)
        printf("%d ",ans[i]);
}