@3 UOJ428 & UOJ461 & UOJ671

[集训队作业2018] 普通的计数题

题目描述

解法

~~调了一年结果发现是输入格式错了，你懂我的感受吗？~~

首先题意转化：每次操作时都会加入一个元素，把第 \(i\) 次加入的元素叫做 \(s_i\)，当且仅当加入 \(1\) 时会删除元素。当加入 \(s_i\) 的时候，把这次操作中删除的 \(s_j\) 都认为是 \(s_i\) 的儿子。这样原来的序列会构成一个森林结构，\(0\) 是叶子 \(1\) 是非叶子，由于最后只会留下一个元素，所以问题转化成有标号树计数。

合法限制是：根标号比子树都大；如果儿子全是叶子，数量 \(B\) 中有；如果儿子存在非叶子，数量 \(A\) 中有。

设 \(f[n]\) 表示大小为 \(n\) 的树的个数（根是 \(1\)），\(g[n]\) 表示大小为 \(n\) 的森林个数（根都是 \(1\)），转移：

\[\begin{aligned} &f[n]=[n-1\in B]+\sum_{i\in A} {n-1\choose i}\cdot g(n-i-1)\\ &g[n]=\sum_{i}{n-1\choose i-1}\cdot f(i)\cdot g(n-i) \end{aligned} \]

熟练的选手可以一眼看出是分治 \(\tt NTT\) 的形式，第一个转移较为常规，可以直接做。但是第二个转移需要 \(f,g\) 互相卷，看上去有点麻烦。

考虑分治区间 \([l,r]\)，需要考虑 \([l,mid]\) 对 \((mid,r]\) 的贡献。那么对于互相卷的问题，应该考察 \(f,g\) 至少一个在 \([l,mid]\) 中，对 \((mid,r]\) 的贡献。可以拆成两部分：

\(g\) 在 \([l,mid]\) 中，\(f\) 在 \([1,mid]\) 中（注意实际上并没有这么长，因为最多取到卷积结果的第 \(r-l\) 项）
\(f\) 在 \([l,mid]\) 中，\(g\) 在 \([1,l)\) 中。

时间复杂度 \(O(n\log^2n)\)

#include <cstdio>
#include <iostream>
using namespace std;
const int M = (1<<18)+5;
#define int long long
const int MOD = 998244353;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,k,fac[M],inv[M],A[M],B[M],rev[M];
int a[M],b[M],c[M],d[M],e[M],f[M],g[M];
void init(int n)
{
	fac[0]=inv[0]=inv[1]=1;
	for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%MOD;
	for(int i=2;i<=n;i++) inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
	for(int i=2;i<=n;i++) inv[i]=inv[i-1]*inv[i]%MOD;
}
int qkpow(int a,int b)
{
	int r=1;
	while(b>0)
	{
		if(b&1) r=r*a%MOD;
		a=a*a%MOD;
		b>>=1;
	}
	return r;
}
void NTT(int *a,int len,int op)
{
	for(int i=0;i<len;i++)
	{
		rev[i]=(rev[i>>1]>>1)|((len/2)*(i&1));
		if(i<rev[i]) swap(a[i],a[rev[i]]);
	}
	for(int s=2;s<=len;s<<=1)
	{
		int t=s/2,w=(op==1)?qkpow(3,(MOD-1)/s):
		qkpow(3,MOD-1-(MOD-1)/s);
		for(int i=0;i<len;i+=s)
			for(int j=0,x=1;j<t;j++,x=x*w%MOD)
			{
				int fe=a[i+j],fo=a[i+j+t];
				a[i+j]=(fe+x*fo)%MOD;
				a[i+j+t]=(fe-x*fo%MOD+MOD)%MOD;
			}
	}
	if(op==1) return ;
	int inv=qkpow(len,MOD-2);
	for(int i=0;i<len;i++) a[i]=a[i]*inv%MOD;
}
void cdq(int l,int r)
{
	if(l==r)
	{
		f[l]=(f[l]+B[l-1])%MOD;
		g[l]=(g[l]+f[l])%MOD;
		return ;
	}
	int mid=(l+r)>>1,len=1;
	cdq(l,mid);
	while(len<=2*(r-l)) len<<=1;
	for(int i=0;i<len;i++) a[i]=b[i]=0;
	for(int i=l;i<=mid;i++)
		a[i-l]=g[i]*inv[i]%MOD;
	for(int i=0;i<r-l;i++)
		b[i]=A[i]*inv[i]%MOD;
	NTT(a,len,1);NTT(b,len,1);
	for(int i=0;i<len;i++)
		c[i]=a[i]*b[i]%MOD;
	NTT(c,len,-1);
	for(int i=mid+1;i<=r;i++)
		f[i]=(f[i]+c[i-l-1]*fac[i-1])%MOD;
	//
	for(int i=0;i<len;i++) b[i]=d[i]=e[i]=0;
	for(int i=1;i<=min(r-l,mid);i++)
		b[i-1]=f[i]*inv[i-1]%MOD;
	for(int i=l;i<=mid;i++)
		d[i-l]=f[i]*inv[i-1]%MOD;
	for(int i=1;i<=min(r-l,l-1);i++)
		e[i-1]=g[i]*inv[i]%MOD;
	NTT(b,len,1);NTT(d,len,1);NTT(e,len,1);
	for(int i=0;i<len;i++)
		c[i]=(a[i]*b[i]+d[i]*e[i])%MOD;
	NTT(c,len,-1);
	for(int i=mid+1;i<=r;i++)
		g[i]=(g[i]+c[i-l-1]*fac[i-1])%MOD;
	cdq(mid+1,r);
}
signed main()
{
	n=read();m=read();k=read();init(n);
	if(n==1) {puts("1");return 0;}
	for(int i=1;i<=m;i++) A[read()]=1;
	for(int i=1;i<=k;i++) B[read()]=1;
	B[0]=0;cdq(1,n);
	printf("%lld\n",(f[n]+MOD)%MOD);
}

新年的Dog划分

题目描述

点此看题

解法

首先考虑已知二分图的情况如何划分二分图的两部，把问题转化成求出原图的一棵生成树。

把 \(m={n\choose 2}\) 条边放在序列上，考虑逐步增加方便利用的已知信息，维护集合 \(S\) 表示已经确定的树边集合。设现在扫描到的边为 \(p\)，我们保留边集 \(S\cup (p,m]\)，如果图仍然联通，那么边 \(p\) 对原图的连通性无影响，直接删掉。如果图不连通，那么把 \(p\) 加入 \(S\) 集合中，然后 \(p\leftarrow p+1\)

线性扫显然太慢，考虑把找树边的过程替换为二分，也就是找到第一个边 \(p\) 满足保留 \(S\cup (p,m]\) 中的边后，图不连通。这样的询问次数是 \(n\log n^2=2n\log n\)，还是不够优秀。

考虑树边的分布十分稀疏，而我们每次基本上都在对整个序列二分，所以会造成次数的浪费。那么把平衡一下复杂度，我们对序列分块，每一块先问一次 删除该块的所有边后是否联通，如果仍然联通那么直接跳过整个块，否则在这个块内二分。一共分成 \(n\) 块，那么询问次数变成了 \(n+n\log n\)

剩下的问题是如何判断二分图，考虑在生成树上给点黑白染色，我们保留黑点和黑点、白点和白点之间的非树边，这些边是可能生成奇环的。那么如何检测奇环呢？我们枚举每一条树边删除，如果图仍然联通，那么就说明有奇环，因为只有奇环才能保持图的连通性，询问次数 \(n\)

总询问次数 \(10n\leq 2000\)

#include "graph.h"
#include <vector>
#include <iostream>
using namespace std;
#define pb push_back
const int M = 205;
int n,a[M][M],d[M];
vector<int> g[M],ans;
vector<pair<int,int>> z,t;
void dfs(int u,int fa)
{
	for(int v:g[u]) if(v^fa)
		d[v]=d[u]^1,dfs(v,u);
}
vector<int> check_bipartite(int vsize)
{
	n=vsize;
	for(int i=0;i<n;i++) for(int p=i+1;p<n;)
	{
		t=z;
		for(int j=p;j<n;j++)
			t.pb({i,j});
		if(query(t)) break;
		int l=p,r=n-1,x=0;
		while(l<=r)
		{
			int mid=(l+r)>>1;t=z;
			for(int j=p;j<=mid;j++)
				t.pb({i,j});
			if(query(t)) l=mid+1;
			else r=mid-1,x=mid;
		}
		g[i].pb(x);g[x].pb(i);
		for(int j=p;j<x;j++) z.pb({i,j});
		p=x+1;
	}
	dfs(0,0);
	for(int i=0;i<n;i++)
		for(int j:g[i]) a[i][j]=1;
	z.clear();
	for(int i=0;i<n;i++)
		for(int j=i+1;j<n;j++)
			if(!a[i][j] && d[i]!=d[j])
				z.pb({i,j});
	for(int i=0;i<n;i++)
		for(int j:g[i]) if(i<j)
		{
			z.pb({i,j});
			if(query(z)) return vector<int>();
			z.pop_back();
		}
	for(int i=0;i<n;i++)
		if(d[i]) ans.pb(i);
	return ans;
}

[UNR #5] 诡异操作

题目描述

点此看题

解法

很容易想到这样一种暴力：对于操作 \(1\)，暴力进行除法；对于操作二，可以把值域拆位，每个二进制位上维护其在区间中的出现次数，and 操作是直接删除一些位，很容易打标记和上传。

时间复杂度 \(O(n\log^2 V)\)，不可接受。复杂度瓶颈在于除法引起拆位高复杂度的重构，思考拆位的本质，其实是维护了一个 \(\log n\cdot \log V\) 的矩阵，显式地维护了这个矩阵的每一列：

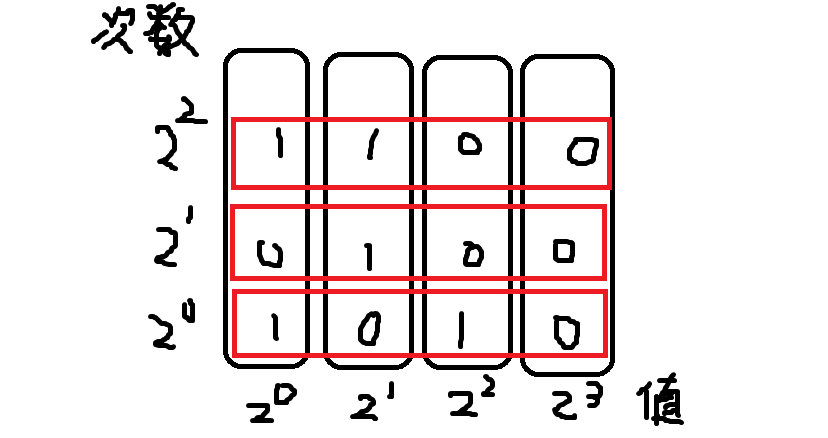
原来我们是按照黑框维护区间中的信息，现在我们切换主体，按照红框维护区间中的信息。注意不要考虑红框的实际意义，就像成要维护这个矩阵，把信息存储在了红框中。

对于红框怎么上传呢？原来的上传方法是左右的黑框单元直接相加得到这个节点的黑框单元，现在我们把左右的红框单元进行不进位加法，然后把进了的位传到下一个红框中（类似大整数加法）

对于红框怎么打标记呢？设 and 上的数是 \(x\)，那么直接把红框单元 and \(x\) 即可，这对应了黑框清零的效果。

对于询问，由于矩阵中 \(1\) 的贡献是行列的二进制相乘，那么直接把红框单元乘上对应 \(2\) 的次幂计入贡献即可。

现在计算时间复杂度，初始每个点的势能都是 \(O(\log V)\)，对整个线段树进行上传操作的复杂度是 \(T(n)=2T(\frac{n}{2})+O(\log n)=O(n)\)，那么额外递归的时间复杂度就是 \(O(n\log V)\)

常规线段树操作的时间复杂度是 \(O(q\log^2 n)\)，总时间复杂度 \(O(n\log V+q\log^2n)\)

总结

弄清维护的对象，然后切换维护的主体，往往可以有奇效！（类似的题目：前进四）

#include <cstdio>
#include <iostream>
using namespace std;
const int M = 4*300005;
#define ll __uint128_t
int n,q,op,L,R,len[M];
ll fl[M],o[M],t[M<<2],*v[M],*id=t;
ll read()
{
    static char buf[100];ll res=0;
	scanf("%s",buf);
    for(int i=0;buf[i];++i)
        res=res<<4|(buf[i]<='9'?buf[i]-'0':buf[i]-'a'+10);
    return res;
}
void output(ll res)
{
    if(res>=16) output(res/16);
    putchar(res%16>=10?'a'+res%16-10:'0'+res%16);
}
void up(int i)
{
	o[i]=o[i<<1]|o[i<<1|1];ll x=0;
	for(int j=0;j<len[i];j++)
	{
		v[i][j]=v[i<<1][j]^v[i<<1|1][j]^x;
		x=(v[i<<1][j]&x)|(v[i<<1|1][j]&x)|
		(v[i<<1][j]&v[i<<1|1][j]);
	}
}
void upd(int i,ll x)
{
	if((o[i]&x)==o[i]) return ;
	o[i]&=x;fl[i]&=x;
	for(int j=0;j<len[i];j++) v[i][j]&=x;
}
void down(int i)
{
	if(~fl[i])
		upd(i<<1,fl[i]),upd(i<<1|1,fl[i]),fl[i]=-1;
}
void build(int i,int l,int r)
{
	fl[i]=-1;
	while((1<<len[i])<=r-l+1) len[i]++;
	v[i]=id;id+=len[i]+1;
	if(l==r) {o[i]=v[i][0]=read();return ;}
	int mid=(l+r)>>1;
	build(i<<1,l,mid);
	build(i<<1|1,mid+1,r);
	up(i);
}
void div(int i,int l,int r,ll x)
{
	if(!o[i] || x==1 || L>r || l>R) return ;
	if(l==r) {o[i]=v[i][0]=o[i]/x;return ;}
	int mid=(l+r)>>1;down(i);
	div(i<<1,l,mid,x);
	div(i<<1|1,mid+1,r,x);
	up(i);
}
void wand(int i,int l,int r,ll x)
{
	if((o[i]&x)==o[i] || L>r || l>R) return ;
	if(L<=l && r<=R) {upd(i,x);return ;}
	int mid=(l+r)>>1;down(i);
	wand(i<<1,l,mid,x);
	wand(i<<1|1,mid+1,r,x);
	up(i);
}
ll ask(int i,int l,int r)
{
	if(L>r || l>R) return 0;
	if(L<=l && r<=R)
	{
		ll r=0;
		for(int j=0;j<len[i];j++)
			r+=v[i][j]<<j;
		return r;
	}
	int mid=(l+r)>>1;down(i);
	return ask(i<<1,l,mid)+ask(i<<1|1,mid+1,r);
}
int main()
{
	scanf("%d %d",&n,&q);
	build(1,1,n);
	while(q--)
	{
		scanf("%d %d %d",&op,&L,&R);
		if(op==1) div(1,1,n,read());
		if(op==2) wand(1,1,n,read());
		if(op==3) output(ask(1,1,n)),puts("");
	}
}

posted @ 2022-07-11 14:50 C202044zxy 阅读(258) 评论(2) 编辑收藏举报

刷新页面返回顶部

C202044zxy

@3 UOJ428 & UOJ461 & UOJ671

[集训队作业2018] 普通的计数题

新年的Dog划分

[UNR #5] 诡异操作

公告