@2 UOJ191 & UOJ422 & UOJ425
[集训队互测2016] Unknown
题目描述
解法
果然是论文题啊,还是很有分量。虽然茴字有四种写法,但是我还是讲解最简单的那一种吧。
看到叉积本能的害怕了,但是数据范围说 \(x\geq 1\),并且根据以前的做题经验,可以转化为这个形式:
问题转化成平面上有若干个点 \((x_i,y_i)\),每次询问用一条斜率为 \(k=\frac{y}{x}\) 的直线去截取这些点,所得到的最大截距乘 \(x\) 就是答案。所以本题的关键就是维护凸包,在凸包上二分就可以得到答案。
考虑这样一种部分分:无2操作,3操作的询问为全部区间,可以直接用二进制分组的方法。即我们类似栈一样维护若干个组,每次插入就向末尾加入一个大小为 \(1\) 的组,如果末尾两个组的大小相同就合并它们。
这样任何时刻场上都只有 \(O(\log n)\) 个组,合并的复杂度为 \(O(n\log n)\),查询的复杂度为 \(O(n\log ^2n)\)
考虑把二进制分组搬到线段树上,也就是说,当左右儿子都满的时候才合并得到这个点的凸包。
但是删除操作很不好搞啊,每次似乎要重构一条链上的凸包,复杂度不可接受。考虑做出这样的改动:对于每一层,我们都允许一个点,在它达到构建的条件时不被构建。
这样对于删除操作,我们直接在包含它的链上打上不能使用的标记;对于加入操作,如果某个点达到了构建的条件,那么我们构建它的上一个点(这样保证每一层都留出一个点不被构建);对于询问操作,如果访问到的点没有被构建,那么直接递归它的儿子。
用势能法证明重构的时间复杂度,设 \(len_i\) 表示第 \(i\) 层带标记组的总长度。打标记的操作会使 \(len_i\) 从 \(0\) 变成 \(2^i\),重构的操作会使得 \(len_i\) 从 \(2^{i+1}\) 变成 \(2^i\);单次插入和删除对于 \(len_i\) 的改变幅度都是 \(1\)
令势能函数 \(E(i)=|len_i-2^i|\),插入删除只会至多有 \(1\) 的贡献,而无论是打标记还是重构都会减少 \(2^i\) 的势能,所以两次重构之间必须要有 \(2^i\) 次插入或删除,那么单层的均摊复杂度是 \(O(n)\),总的均摊复杂度是 \(O(n\log n)\)
对于询问,考虑区间 \([l,r]\) 至多被拆分到一个被打标记的点,此时会被分解为 \(O(\log n)\) 个点,所以时间复杂度还是 \(O(n\log ^2n)\)
总时间复杂度 \(O(n\log^2 n)\),使用 \(\tt zkw\) 线段树实现较为方便。空间复杂度 \(O(n\log n)\),需要用指针分配来精细实现。
总结
对于只在末尾插入\(/\)末尾删除的题目,把二进制分组放在线段树上是通用做法。
#include <cstdio>
#include <iostream>
using namespace std;
const int mx = 1<<19;
const int M = 300005;
const int MOD = 998244353;
#define ll long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
struct node
{
int x,y;
node(int X=0,int Y=0) : x(X) , y(Y) {}
friend ll operator * (node a,node b)
{return (ll)a.x*b.y-(ll)b.x*a.y;}
friend node operator - (node a,node b)
{return node(a.x-b.x,a.y-b.y);}
}nd[20][M],*h[mx+M],*a;
int n,m,ans,tp,siz[mx+M];
void ins(node t)
{
if(tp==1 && t.x==a->x)
{
if(t.y<=a->y) return ;
tp--;
}
while(tp>1 && (a[tp-1]-a[tp-2])*(t-a[tp-1])>=0)
tp--;
a[tp++]=t;
}
void build(int x)
{
if(x<=0 || siz[x]) return ;//has been built
a=h[x];tp=0;
node *px=h[x<<1],*A=px+siz[x<<1];
node *py=h[x<<1|1],*B=py+siz[x<<1|1];
while(px<A && py<B)
{
if(px->x<=py->x) ins(*px),px++;
else ins(*py),py++;
}
while(px<A) ins(*px),px++;
while(py<B) ins(*py),py++;
siz[x]=tp;
}
void push()
{
int x=read(),y=read(),u=(++n)+mx;
siz[u]=1;*h[u]=node(x,y);
for(int p=u;p&1;p>>=1,build(p-1));
//p should not be built , p-1 should be built
}
void pop()//just tag it
{
for(int p=(n--)+mx>>1;siz[p]>0;p>>=1) siz[p]=0;
}
ll get(int x,node t)
{
if(siz[x]<=0) return max(get(x<<1,t),get(x<<1|1,t));
int l=0,r=siz[x]-1;ll res=-(1ll<<60);a=h[x];
while(l+4<r)
{
int mid=(l+r)>>1;
ll c1=t*a[mid],c2=t*a[mid+1];
res=max(res,max(c1,c2));
if(c1<=c2) l=mid+1;
else r=mid-1;
}
while(l<=r) res=max(res,t*a[l]),l++;
return res;
}
int ask()
{
ll res=-(1ll<<60);node t;
int l=read()+mx-1,r=read()+mx+1;
t.x=read();t.y=read();
for(;l^r^1;l>>=1,r>>=1)
{
if((l&1)==0) res=max(res,get(l^1,t));
if(r&1) res=max(res,get(r^1,t));
}
return (res%MOD+MOD)%MOD;
}
void init()
{
for(int l=mx,r=mx+min(M-5,m),d=0;l;l>>=1,r>>=1,d++)
for(int i=l;i<=r;i++)//distribute size
h[i]=nd[d]+(i-l<<d),siz[i]=0;
for(int i=mx;i;i>>=1) siz[i]=-1;//ban
}
signed main()
{
read();
while(m=read())
{
init();ans=n=tp=0;
while(m--)
{
int op=read();
if(op==1) push();
if(op==2) pop();
if(op==3) ans^=ask();
}
printf("%d\n",ans);
}
}
[集训队作业2018] 小Z的礼物
题目描述
解法
考虑 \(\min-\max\) 反演:
问题在于求出带容斥系数的 \(E(\min(T))\),设 \(c(T)\) 表示只考虑 \(T\) 集合中的物品,有多少种选取方法可以选到这些物品,设 \(t=2nm-n-m\) 表示可能的选取方式,那么 \(E(\min(T))=\frac{c(T)}{t}\)
直接 \(dp\) 计算容斥系数,设 \(f(i,j,s,k)\) 表示考虑到点 \((i,j)\),现在轮廓线的状态是 \(s\),已经积累的选取方案数是 \(k\),转移讨论这个点选还是不选,如果选的话带上 \(-1\) 的容斥系数,可以结合下图来理解转移过程:
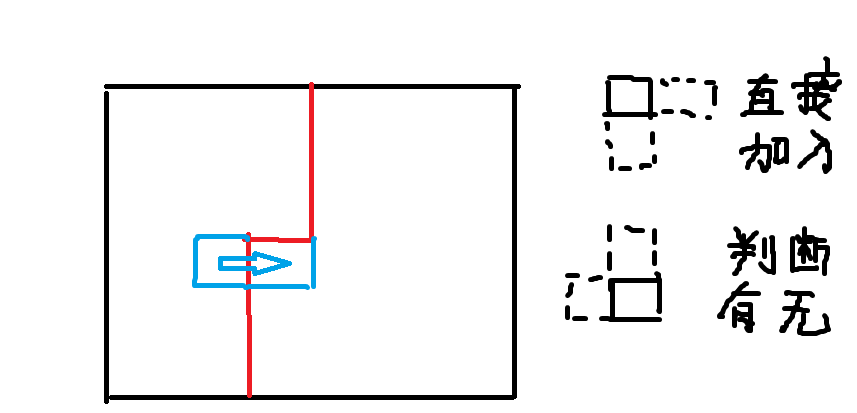
时间复杂度 \(O(n^2m^2\cdot 2^n)\),所以遇见这种简单的插头 dp 就不要怕,直接上。
#include <cstdio>
#include <cstring>
const int MOD = 998244353;
const int M = 1205;
#define ll long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,t,ans,inv[M];char p[M][M];
int f[1<<6][M],g[1<<6][M];
void add(int &x,int y) {x=(x+y)%MOD;}
signed main()
{
n=read();m=read();t=2*n*m-n-m;
for(int i=1;i<=n;i++) scanf("%s",p[i]+1);
inv[0]=inv[1]=1;
for(int i=2;i<=t;i++)
inv[i]=(ll)inv[MOD%i]*(MOD-MOD/i)%MOD;
f[0][0]=MOD-1;
for(int i=1;i<=m;i++) for(int j=1;j<=n;j++)
{
memcpy(g,f,sizeof f);
memset(f,0,sizeof f);
for(int s=0;s<(1<<n);s++)
for(int k=0;k<=t;k++) if(g[s][k])
{
int ns=s&((1<<n)-1-(1<<j-1));
add(f[ns][k],g[s][k]);
if(p[j][i]=='.') continue;
ns|=(1<<j-1);int nk=k;
nk+=(i<m);nk+=(j<n);
if(i>1 && !(s>>(j-1)&1)) nk++;
if(j>1 && !(s>>(j-2)&1)) nk++;
add(f[ns][nk],MOD-g[s][k]);
}
}
for(int s=0;s<(1<<n);s++)
for(int i=1;i<=t;i++)
add(ans,(ll)f[s][i]*inv[i]%MOD);
ans=(ll)ans*t%MOD;
printf("%d\n",ans);
}
[集训队作业2018] strings
题目描述
解法
考虑折半搜索,对于前半段 \(m=\lfloor\frac{n}{2}\rfloor\),我们处理出每一种可以对应哪些模板串,时间复杂度 \(O(q\cdot m\cdot 2^m)\)
对于每一个模板串,我们处理出它对应哪些后半段,时间复杂度 \(O(q\cdot m\cdot 2^m)\)
考虑套上 bitset,即枚举每一个前半段,再枚举匹配到的模式串,用 bitset 储存对应的后半段,时间复杂度 \(O(\frac{q\cdot 2^n}{w})\)
复杂度瓶颈是枚举模式串,考虑类似四毛子一样分块,设块长为 \(B\),每一块内预处理出块内模式串的所有子集,对应的 bitset,时间复杂度 \(O(\frac{q\cdot 2^{m+B}}{w})\)
那么我们就不需要枚举模式串,对于每个块,处理出子集后用处理的结果查询即可,时间复杂度 \(O(\frac{q\cdot 2^n}{wB})\)
取 \(B=10\),总时间复杂度 \(O(\frac{q\cdot 2^{n}}{10\cdot w})\)
#include <cstdio>
#include <bitset>
#include <iostream>
using namespace std;
const int M = 105;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m1,m2,q,s,ans;char c[M][M];
bitset<1<<15> a[M],b[10][1<<10],nw;
int equal(char c,int x) {return c==x+'0' || c=='?';}
signed main()
{
n=read();q=read();
m1=n>>1;m2=n-m1;s=10;
for(int i=0;i<q;i++)
scanf("%s",c[i]);
for(int i=0;i<q;i++) for(int j=0;j<(1<<m2);j++)
{
int f=1;
for(int k=0;k<m2;k++)
f&=equal(c[i][m1+k],j>>k&1);
a[i][j]=f;
}
for(int i=0;i*s<q;i++)
{
int l=i*s,r=min(l+s,q);
for(int j=0;j<(1<<s);j++)
for(int k=l;k<r;k++)
if(j>>(k-l)&1) b[i][j]|=a[k];
}
//
for(int j=0;j<(1<<m1);j++)
{
nw.reset();
for(int i=0;i*s<q;i++)
{
int l=i*s,r=min(l+s,q),t=0;
for(int k=l;k<r;k++)
{
int f=1;
for(int x=0;x<m1;x++)
f&=equal(c[k][x],j>>x&1);
t|=f<<(k-l);
}
nw=nw|b[i][t];
}
ans+=nw.count();
}
printf("%d\n",ans);
}



