[做题笔记] 1373452814 的 dp 选讲

[AGC056B] Range Argmax

题目描述

点此看题

给定 $n,m$ ，有 $m$ 个 $[1,n]$ 的子区间，第 $i$ 个区间为 $[l_i,r_i]$

对于一个 $n$ 阶排列 $p$ ，令 $x_i$ 为 $p_{l_i}...p_{r_i}$ 中最大值的下标。

排列可以任取，求本质不同的序列 $\{x\}$ 的数量，答案对 $998244353$ 取模。

$n\leq 300$

解法

考虑得到序列 $\{x\}$ 的方式，其实就是在笛卡尔树上 $\tt dfs$ ，每次确定包含当前点区间的 $x_i$ ，然后把这些区间全部删掉。

得到删除序列是容易的，考虑如何把删除序列和 $\{x\}$ 一一对应，只需要满足下面两个条件即可：

删除当前点之后，由于左右两边独立，强制先递归左边，再递归右边。
当前删除点是所有能得到这个 $\{x\}$ 序列的删除方式中，位置最左的删除点。

翻译一下第二个条件，考虑当前点 $a$ 的左儿子 $b$ ，设 $lb$ 表示包含 $a$ 的区间最小的左端点，如果 $b<lb$ ，那么显然先删除 $b$ 也可以得到同样的 $\{x\}$ ；但如果 $b\geq lb$ ，先删除 $b$ 就会得到不同的 $\{x\}$ ，所以这会增加限制： $b\geq lb$

根据上面的限制来 $dp$ ，设 $dp[l][r][x]$ 表示只考虑导出区间 $[l,r]$ ， $a\geq x$ 的方案数，转移：

d p [l] [r] [a] \leftarrow \sum_{x \geq a} d p [l] [x - 1] [l b [l] [r] [x]] \cdot d p [x + 1] [r] [x + 1]

$dp[l][r][a]\leftarrow \sum _{x\geq a} dp[l][x-1][lb[l][r][x]]\cdot dp[x+1][r][x+1]$

其中 $lb[l][r][a]$ 表示只考虑导出区间 $[l,r]$ ，包含 $a$ 的区间最小的左端点。使用前缀和优化，时间复杂度 $O(n^3)$

#include <cstdio>
const int M = 305;
const int MOD = 998244353;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,b[M],v[M][M],a[M][M][M],dp[M][M][M];
signed main()
{
	n=read();m=read();
	for(int i=1;i<=m;i++)
	{
		int l=read(),r=read();
		v[l][r]=1;
	}
	for(int r=1;r<=n;r++)
	{
		for(int l=1;l<=r;l++)
			if(v[l][r]) b[l]=r;
		for(int l=r;l>=1;l--)
		{
			for(int i=1;i<=n;i++)
				a[l][r][i]=a[l+1][r][i];
			for(int i=l;i<=b[l];i++)
				a[l][r][i]=l;
		}
	}
	for(int i=0;i<=n;i++) for(int l=1;l+i-1<=n;l++)
	{
		int r=l+i-1,f=0;
		for(int i=l;i<=r;i++) f|=a[l][r][i];
		if(!f)
		{
			for(int i=l-1;i<=r+1;i++)
				dp[l][r][i]=1;
			continue;
		}
		for(int i=l;i<=r;i++) if(a[l][r][i])
			dp[l][r][i]=1ll*dp[l][i-1][a[l][r][i]]*
			dp[i+1][r][i+1]%MOD;
		for(int i=r-1;i>=l;i--)
			dp[l][r][i]=(dp[l][r][i]+dp[l][r][i+1])%MOD;
	}
	printf("%d\n",dp[1][n][1]);
}

[AGC040E] Prefix Suffix Addition

题目描述

点此看题

解法

首先考虑只有操作一时怎么做？考虑差分数组 $b_i=x_{i+1}-x_{i}$ ，那么操作一的效果是：把 $b_k$ 减少 $c_k$ ，增加 $b_{0},b_1...b_{k-1}$ ，并且满足增加的总和是 $c_k$

转化之后很容易得到答案下界，因为 $b_i<0$ 都必须作为 $b_k$ 被我们操作一次，所以答案下界就是 $\sum_{i=0}^n [a_i>a_{i+1}]$ ，因为序列非负，所以每个位置的差分后缀和非正，那么只要我们贪心地增加靠后的 $b_i$ ，就可以构造出解。

只有操作二时是类似的，答案下界是 $\sum_{i=0}^n [a_i<a_{i+1}]$

由于操作一和操作二是独立的，可以把他们分开来考虑。问题可以转化成：找到一种拆分方式 $b_i+c_i=a_i$ ，最小化代价：

\sum_{i = 0}^{n} [b_{i} > b_{i + 1}] + [c_{i} < c_{i + 1}]

$\sum_{i=0}^n [b_i>b_{i+1}]+[c_i<c_{i+1}]$

设 $dp[i][j]$ 表示考虑前 $i$ 个位置，满足 $c_i=j$ 的最小代价。但是这样状态数就直接爆炸，可以搞一些 $\tt observations$ ：

观察代价的形式，发现 $dp[i]$ 随着 $j$ 的增大而增大。
由于上一个转移点是任意的，所以 $dp[i]$ 的极差不超过 $2$

那么我们可以用一个分段函数来替代我们的 $dp$ 数组，也就是维护 $dp,f_0,f_1$ ，表示现在的基准值（最小 $dp$ 值）是 $dp$ ，满足 $j\in [0,f_0]$ 时取 $dp$ ； $j\in(f_0,f_1]$ 时取 $dp+1$ ； $j\in(f_1,a_i]$ 时取 $dp+2$

如果 $a_i\geq a_{i-1}$ ， $[0,f_0]$ 这一段可以直接平移下来，不会有额外的贡献，但是基准值的范围也不能右移，因为右移后如果又要从上一层的 $[0,f_0]$ 转移过来会有额外的贡献。

考虑 $f_0$ 这个点的对基准值 $+1$ 的影响，由于不能有 $[b_i>b_{i+1}]$ 的贡献，即必须满足 $a_{i-1}-f_0\leq a_i-p$ ，解得 $p\leq f_0+a_i-a_{i-1}$ ，那么基准值 $+1$ 的范围就变成了 $(f_0,\max(f_1,f_0+a_{i}-a_{i-1})]$

如果 $a_i<a_{i-1}$ ，为了避免 $[b_i>b_{i+1}]$ 的贡献，基准值的范围变成了 $[0,f_0+a_{i}-a_{i-1}]$ ，基准值 $+1$ 的范围变成了 $(f_0+a_{i}-a_{i-1},\max(f_0,f_1+a_{i}-a_{i-1}))$ ，注意如果新的 $f_0<0$ ，那么要把基准值增加 $1$ ，并且让 $f_0\leftarrow f_1$

最后还要添加 $[b_n>b_{n+1}]+[c_n<c_{n+1}]$ 的贡献，即 $[a_n-f_0>0]$ ，时间复杂度 $O(n)$

总结

最后讨论法优化 $dp$ 的技巧很厉害，类似的题目还有：Split

#include <cstdio>
#include <iostream>
using namespace std;
const int M = 200005;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,f0,f1,dp,ls,a[M];
signed main()
{
	n=read();
	for(int i=1;i<=n;i++)
	{
		int v=read();
		if(v>=ls) f1=max(f1,f0+v-ls);
		else
		{
			f1=max(f0,f1-ls+v);
			f0+=v-ls;
			if(f0<0) dp++,f0=f1,f1=v;
		}
		f0=min(f0,v);f1=min(f1,v);ls=v;
	}
	printf("%d\n",dp+(ls>f0));
}

Evacuation

题目描述

点此看题

有 $1,2...n$ 排成一列，第 $i$ 个位置可以容纳 $a_i$ 个人。给出一个非负整数 $m$ ，定义一个位置的代价为初始有 $m$ 个人在这个位置上，可以让人移动到其他位置，所有人都可以被容纳的最小总移动距离。

有 $q$ 次询问，每次给出区间 $[l,r]$ ，一个人走到区间外视为被容纳，问 $[l,r]$ 所有位置代价的最大值。

$n,q\leq 2\cdot 10^5$

解法

一些人会走到边界外，但是只会走到最近的一个边界外。所以对于询问 $[l,r]$ ， $x\in [l,mid]$ 会把 $l$ 当成边界， $x\in(mid,r]$ 会把 $r$ 当成边界。设 $f(x,l)$ 表示初始 $m$ 个人都在 $x$ 位置，左边界是 $l$ 的最小移动总距离，它可以表示成：

\sum_{i = 0}^{x - l} max (0, m - \sum_{| x - j | \leq i} a_{j})

$\sum_{i=0}^{x-l} \max(0,m-\sum_{|x-j|\leq i}a_j)$

可以把 $l$ 修正到不会取 $0$ （预处理 $r[x]$ 表示最小的不会取 $0$ 的 $l$ ），正贡献是 $m\cdot (x-l+1)$ ，对于负贡献，中间的 $x$ 贡献 $x-l+1$ 次，并且依次向两边递减。预处理 $s[x]=\sum_{i=1}^x a_i,sum[x]=\sum_{i=1}^x i\cdot a_i$ 就可以 $O(1)$ 计算任意的 $f$

一个重要的 $\tt observation$ 是：对于 $l$ ， $x$ 满足决策单调性，即 $l$ 增大时最优 $x$ 的取值不降，证明：

只需要证明 $f(x,l)+f(x+1,l+1)\geq f(x,l+1)+f(x+1,l)$ 即可，由于：

$f(x,l)-f(x,l+1)=\max(0,m-\sum_{|x-j|\leq x-l} a_j)$
$f(x+1,l)-f(x+1,l+1)=\max(0,m-\sum_{x-j\leq x-l+1} a_j)$
可以发现第一个求和区间被第二个包含，那么上面显然更大，所以有：

$f(x,l)-f(x,l+1)\geq f(x+1,l)-f(x+1,l+1)$
移项之后就可以得到决策单调性的关键式子：

$f(x,l)+f(x+1,l+1)\geq f(x,l+1)+f(x+1,l)$

由于询问可以转化成：对于固定的 $l$ ， $x$ 被限制在一个区间内的最大代价。我们可以把所有询问拆分到线段树上，然后对于线段树上的一个节点，暴力跑分治实现的决策单调性。

对于右边界 $r$ 的情况，只需要把所有东西都翻转，然后同样跑一次就行了，时间复杂度 $O(n\log ^2n)$

#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 200005;
#define int long long
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,q,a[M],qx[M],qy[M],ans[M];
int s[M],sum[M],r[M];vector<int> v,p[M<<2];
void ins(int i,int l,int r,int L,int R,int x)
{
	if(L>r || l>R) return ;
	if(L<=l && r<=R) {p[i].push_back(x);return ;}
	int mid=(l+r)>>1;
	ins(i<<1,l,mid,L,R,x);
	ins(i<<1|1,mid+1,r,L,R,x);
}
int ask(int l,int x)
{
	l=max(l,x-r[x]+1);
	return (m-s[2*x-l]+s[l-1])*(x-l+1)
	+x*(s[x]-s[l-1])-(sum[x]-sum[l-1])
	-x*(s[2*x-l]-s[x])+(sum[2*x-l]-sum[x]);
}
void cdq(int l,int r,int ql,int qr)
{
	if(ql>qr) return ;
	int mid=(ql+qr)>>1,id=v[mid],p=l,mx=0;
	for(int i=l;i<=r;i++) if(ask(qx[id],i)>mx)
		mx=ask(qx[id],i),p=i;
	ans[id]=max(ans[id],mx);
	cdq(l,p,ql,mid-1);cdq(p,r,mid+1,qr);
}
int cmp(int x,int y) {return qx[x]<qx[y];}
void dfs(int i,int l,int r)
{
	if(!p[i].empty())
	{
		v=p[i];sort(v.begin(),v.end(),cmp);
		cdq(l,r,0,v.size()-1);
	}
	if(l==r) return ;
	int mid=(l+r)>>1;
	dfs(i<<1,l,mid);dfs(i<<1|1,mid+1,r);
}
void work()
{
	for(int i=1;i<=4*n;i++) p[i].clear();
	for(int i=1;i<=q;i++)
		ins(1,1,n,qx[i],(qx[i]+qy[i])/2,i);
	for(int i=1;i<=n;i++)
		s[i]=s[i-1]+a[i],sum[i]=sum[i-1]+i*a[i];
	for(int i=1;i<=n;i++)
	{
		r[i]=max(r[i-1]-1,1ll);
		while(i+r[i]<=n && i>r[i] &&
		s[i+r[i]]-s[i-r[i]-1]<=m) r[i]++;
	}
	dfs(1,1,n);
}
signed main()
{
	n=read();m=read();
	for(int i=1;i<=n;i++) a[i]=read();
	q=read();
	for(int i=1;i<=q;i++) qx[i]=read(),qy[i]=read();
	work();
	reverse(a+1,a+1+n);
	for(int i=1;i<=q;i++) qx[i]=n-qx[i]+1,
		qy[i]=n-qy[i]+1,swap(qx[i],qy[i]);
	work();
	for(int i=1;i<=q;i++) printf("%lld\n",ans[i]);
}

[AGC049E] Increment Decrement

题目描述

点此看题

解法

首先考虑对于固定的 $a$ ，如何计算答案。

如果只有第一种操作，那么答案 $\sum |a_i|$

如果只有第二种操作，考虑差分数组，不难发现答案为 $\sum c\cdot \max(a_{i+1}-a_i,0)$

把这两种操作的影响拆分，设第二种操作对位置 $i$ 的影响为 $y_i$ ，则问题转化成找到一组 $y$ ，最小化：

\sum | a_{i} - y_{i} | + c \cdot max (y_{i + 1} - y_{i}, 0)

$\sum |a_i-y_i|+c\cdot \max(y_{i+1}-y_i,0)$

设 $dp(i,j)$ 表示考虑前 $i$ 个位置， $y_i=j$ 的最小代价，转移：

d p (i, j) = | a_{i} - j | + min_{x} (d p (i - 1, x) + c \cdot max (j - x, 0))

$dp(i,j)=|a_i-j|+\min_{x} (dp(i-1,x)+c\cdot \max(j-x,0))$

略微调整一下状态定义，把 $|a_i-j|$ 这个代价的计算放在 $i+1$ 处，转移变成：

d p (i, j) = min_{x} {d p (i - 1, x) + | a_{i - 1} - x | + c \cdot max (j - x, 0)}

$dp(i,j)=\min_{x} \{dp(i-1,x)+|a_{i-1}-x|+c\cdot \max(j-x,0)\}$

初始化 $dp(1,j)=c\cdot \max(j,0)$ ，答案是 $dp(n+1,0)$

可以用归纳法证明 $dp(i,...)$ 是凸函数，首先 $dp(1,...)$ 是凸函数，然后考虑 $dp(i-1)$ 向 $dp(i)$ 转移时，首先加上了一个绝对值函数 $|a_{i-1}-x|$ ，然后又和 $f(x)=c\cdot \max(x,0)$ 进行了 $\min$ 卷积，执行这些操作后还是凸函数。

这时候就可以直接上 $\tt slope\ trick$ 了，考虑维护 $0$ 处的点值 $v_0$ 和描述斜率变化的集合 $S$ ，对于添加 $|a_{i-1}-x|$ 这个绝对值函数，我们首先把 $v_0$ 加上 $a_{i-1}$ ，然后向 $S$ 中添加两个 $a_{i-1}$ 处的转折点。

稍微麻烦一下的操作是和 $f(x)$ 进行 $\min$ 卷积。回忆两个凸函数是如何进行 $\min$ 卷积的，实际上就是类似归并排序，选择添加增量少的部分。效果如下图，一句话概括就是掐头去尾：

我们取出最小的转折点 $a$ 和最大的转折点 $b$ ，首先把 $v_0$ 减去 $a$ ，从 $S$ 中删除 $a$ 就可以使得开头段的斜率变为 $0$ ；然后从 $S$ 中删除 $b$ 就可以使得结尾段的斜率变为 $c$

现在回到计数问题上来，发现加的部分是固定的，主要的减的部分不好计算。可以考虑拆贡献，我们把所有权值 $b$ 都离散化，每次把小于 $b_i$ 的权值设置为 $0$ ，把 $\geq b_i$ 的权值设置为 $1$ ，只需要统计取出 $1$ 的个数，乘上 $(b_{i}-b_{i-1})$ 就是贡献。

设 $f(i,j)$ 表示前 $i$ 次操作，现在 $S$ 中有 $j$ 个 $0$ 的方案数， $g(i,j)$ 表示对应取出 $1$ 的总个数。

转移就暴力添加 $0/1$ ，模拟 $\tt slope \ trick$ 的过程即可，时间复杂度 $O(nk\cdot nc)=O(n^2kc)$

总结

如果各种操作独立，可以单独分析各种操作，然后枚举不同操作的影响，就可以方便地计算代价。

看到 $|...|,\max(...)$ 等凸函数复合时，一定要本能地联想到 $\tt slope \ trick$

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 105;
const int MOD = 1e9+7;
#define int long long
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,c,k,ans,sub,h[M],f[M][M],g[M][M];
pair<int,int> b[M*M];
void add(int &x,int y) {x=(x+y)%MOD;}
signed main()
{
	n=read();c=read();k=read();
	for(int i=1;i<=n;i++) for(int j=1;j<=k;j++)
	{
		int x=read();add(ans,x);
		b[(i-1)*k+j]=make_pair(x,i);
	}
	sort(b+1,b+1+n*k);
	for(int w=1;w<=n*k;w++)
	{
		for(int i=0;i<=n;i++) for(int j=0;j<=n;j++)
			f[i][j]=g[i][j]=0;
		f[0][c]=1;
		for(int i=1;i<=n;i++) for(int j=0;j<=c;j++)
		for(int t=0;t<2;t++)
		{
			int vl=t?h[i]:k-h[i],tj=j+2*t;
			int f1=f[i-1][j]*vl%MOD,f2=g[i-1][j]*vl%MOD;
			if(tj) tj--;
			else f2=(f2+f1)%MOD;
			tj=min(tj,c);
			add(f[i][tj],f1);add(g[i][tj],f2);
		}
		for(int i=0;i<=n;i++)
			add(sub,g[n][i]*(b[w].first-b[w-1].first));
		h[b[w].second]++;
	}
	for(int i=1;i<n;i++) ans=ans*k%MOD;
	printf("%lld\n",(ans-sub+MOD)%MOD);
}

[JOISC 2017 Day 2] 火车旅行

题目描述

点此看题

解法

考虑两个点 $i,j$ 可以一步到达的条件： $\max_{i=l+1}^{r-1} v_i<\min(v_i,v_j)$

我们从 $v_i,v_j$ 较小的一侧考虑，对于每个 $i$ 找到左边第一个权值大于等于它的点 $l_i$ ，右边第一个权值大于等于它的点 $r_i$ ，那么我们连边 $(l_i,i)$ 和 $(i,r_i)$ ，在这个图上跑最短路就可以得到答案。

暴力最短路显然会超时，考虑换一种方式来构建这张图——按照权值从大到小加入点，每次添加若干条链。比如对于样例，我们先加入 1-8-9，再加入 1-5-6-7-8，最后加入 1-2-3-4-5，把边当成点，会构成这样的树形结构：

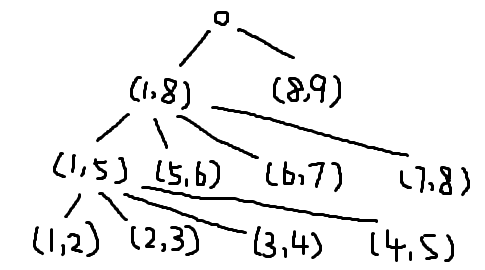
发现我们从某个点走若干步时，一定会经过树上祖先的两点之一。把问题转化到树上时，我们只需要维护到左端点的最小距离和到右端点的最小距离，跳一步父亲相当于乘上一个 $2\times 2$ 的矩阵转移。

那么对于 $a,b$ 两点的询问，我们先让它们跳到 $\tt lca$ 的儿子处，然后在环上找最短距离即可。

由于本题的边权为 $1$ ，所以两个步骤可以合为一体。首先倍增预处理 $L[i][j]/R[i][j]$ 表示跳 $2^j$ 可以到达的最远左端点 $/$ 最远右端点，处理询问时，如果覆盖范围没有到另一个点，就直接暴力跳。

时间复杂度 $O(n\log n)$

#include <cstdio>
#include <iostream>
using namespace std;
const int M = 100005;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,q,a[M],s[M],L[M][20],R[M][20];
signed main()
{
	n=read();read();q=read();
	for(int i=1;i<=n;i++) a[i]=read();
	for(int i=1;i<=n;i++)
	{
		while(m && a[s[m]]<a[i]) m--;
		L[i][0]=m?s[m]:i;s[++m]=i;
	}
	m=0;
	for(int i=n;i>=1;i--)
	{
		while(m && a[s[m]]<a[i]) m--;
		R[i][0]=m?s[m]:i;s[++m]=i;
	}
	L[0][0]=0;R[n+1][0]=n+1;
	for(int j=1;j<20;j++)
		for(int i=0;i<=n+1;i++)
		{
			L[i][j]=min(L[L[i][j-1]][j-1],L[R[i][j-1]][j-1]);
			R[i][j]=max(R[L[i][j-1]][j-1],R[R[i][j-1]][j-1]);
		}
	while(q--)
	{
		int a=read(),b=read(),ans=0;
		if(a>b) swap(a,b);
		int l=a,r=a;
		for(int i=19;i>=0;i--)
		{
			int nl=min(L[l][i],L[r][i]);
			int nr=max(R[l][i],R[r][i]);
			if(nr<b) l=nl,r=nr,ans+=(1<<i);
		}
		a=r;l=r=b;
		for(int i=19;i>=0;i--)
		{
			int nl=min(L[l][i],L[r][i]);
			int nr=max(R[l][i],R[r][i]);
			if(a<nl) l=nl,r=nr,ans+=(1<<i);
		}
		printf("%d\n",ans);
	}
}

posted @ 2022-07-01 19:23 C202044zxy 阅读(764) 评论(2) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· [TJOI2018] 游园会

· [省选集训2022] 模拟赛6

· 【学习笔记】NOIP模拟赛

· AGC056B Range Argmax 题解

· 区间 dp

阅读排行：
· 无需6万激活码！GitHub神秘组织3小时极速复刻Manus，手把手教你使用OpenManus搭建本
· Manus爆火，是硬核还是营销？
· 终于写完轮子一部分：tcp代理了，记录一下
· 别再用vector＜bool＞了！Google高级工程师：这可能是STL最大的设计失误
· 单元测试从入门到精通

C202044zxy

[做题笔记] 1373452814 的 dp 选讲

[AGC056B] Range Argmax

[AGC040E] Prefix Suffix Addition

Evacuation

[AGC049E] Increment Decrement

[JOISC 2017 Day 2] 火车旅行

公告

搜索

常用链接

随笔分类

最新评论