[冲刺国赛2022] 模拟赛10
寄
题目描述
有一棵 \(n\) 个点的树，边有边权。有 \(m\) 个关键点 \(a_1,a_2...a_m\)（这些关键点可重），你需要选择若干个中转站 \(p_1,p_2...p_k\)，选择中转站的代价是 \(k\cdot C\)，每个关键点的代价是到最近中转站的距离，最小化代价和。
\(n\leq 3000\)
解法
直接记录到中转站的距离不好做，我们不妨直接记录到管辖某个点的中转站的距离。
设 \(dp[u][i]\) 表示管辖点 \(u\) 的中转站是 \(i\)，子树 \(u\) 内的最小代价和。转移考虑加入一个子树 \(v\)，考虑管辖 \(u,v\) 的中转站要么相同，要么在 \(v\) 的子树内，我们在第二种情况加上 \(C\) 的权值即可：
为了方便转移我们其实放宽了限制，不合法的转移一定是不优的。
初始化 \(dp[u][i]=dis(u,i)\)，最后的答案是 \(\min dp[1][i]+C\)，时间复杂度 \(O(n^2)\)
其中这题就是 Red and Black Tree 的超级弱化版，不知道我为什么做不出来。
#include <cstdio>
#include <iostream>
using namespace std;
const int M = 3005;
#define int long long
const int inf = 1e18;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,C,ans,tot,f[M],a[M],dp[M][M];
struct edge{int v,c,next;}e[M<<1];
void get(int rt,int u,int fa)
{
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v,c=e[i].c;
if(v==fa) continue;
dp[rt][v]=dp[rt][u]+c;
get(rt,v,u);
}
}
void dfs(int u,int fa)
{
for(int i=1;i<=n;i++) dp[u][i]*=a[u];
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v,c=e[i].c;
if(v==fa) continue;
dfs(v,u);
int mi=inf;
for(int j=1;j<=n;j++)
mi=min(mi,dp[v][j]);
for(int j=1;j<=n;j++)
dp[u][j]+=min(dp[v][j],C+mi);
}
}
signed main()
{
freopen("post.in","r",stdin);
freopen("post.out","w",stdout);
n=read();m=read();C=read();
for(int i=1;i<n;i++)
{
int u=read(),v=read(),c=read();
e[++tot]=edge{v,c,f[u]},f[u]=tot;
e[++tot]=edge{u,c,f[v]},f[v]=tot;
}
for(int i=1;i<=m;i++) a[read()]++;
for(int i=1;i<=n;i++) get(i,i,0);
dfs(1,0);ans=inf;
for(int i=1;i<=n;i++)
ans=min(ans,dp[1][i]+C);
printf("%lld\n",ans);
}
润
题目描述
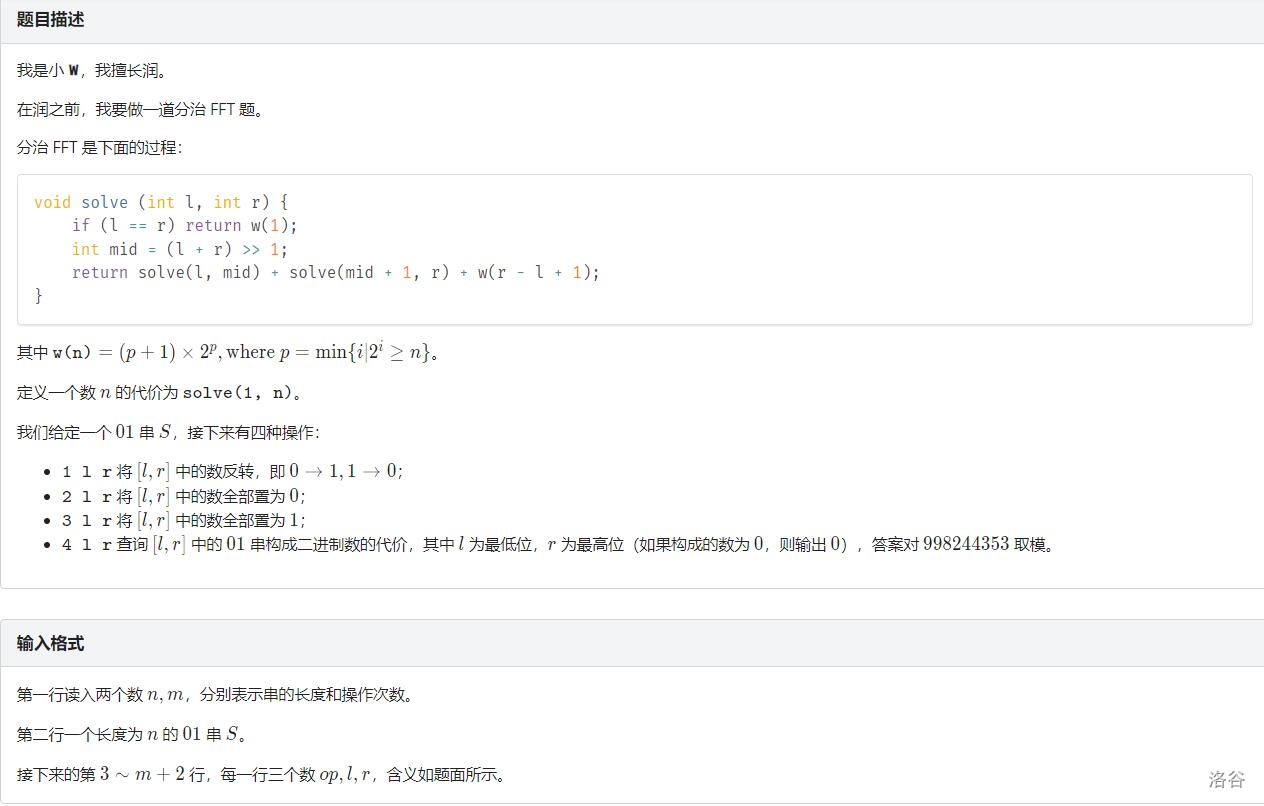
解法
有这样的性质：当我们把 \(solve(n)\) 推到 \(solve(n+1)\) 时，增量是 \(w(0)+w(\max(n)-\sec(n))\)，其中 \(\max(n)\) 表示 \(n\) 二进制位的最高位，\(\sec(n)\) 表示 \(n\) 二进制的次高位，特别地，如果没有次高位那么 \(\sec(n)=-1\)
设 \(f=\max(n),g=\sec(n)\)，考虑增量法，首先选取 \(2^f\) 为起点，直接计算它的值：
\(2^f\) 增量到 \(2^f+1\) 需要特殊考虑，设 \(dt(x)=w(x)+w(0)\)，那么增量是 \(dt(f+1)\)；然后从 \(2^f+1\) 增量到 \(2^f+2^g\)，我们枚举二进制的次高位：
最后考虑从 \(2^f+2^g\) 增量到 \(n\)，由于最高位和次高位已经确定了，此时可以直接计算：
那么线段树就只需要支持区间查询二进制数，寻找区间的最后一个 \(1\)（直接线段树上二分），这是极其易于维护的，时间复杂度 \(O(n\log n)\)
#include <cstdio>
const int M = 100005;
const int N = M<<2;
const int MOD = 998244353;
const int inv2 = (MOD+1)/2;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,a[M],pw[M],inv[M],s[N],fl[N],cov[N],all[N];
void build(int i,int l,int r)
{
cov[i]=-1;
if(l==r)
{
all[i]=pw[l];
s[i]=(a[l]?pw[l]:0);
return ;
}
int mid=(l+r)>>1;
build(i<<1,l,mid);
build(i<<1|1,mid+1,r);
s[i]=(s[i<<1]+s[i<<1|1])%MOD;
all[i]=(all[i<<1]+all[i<<1|1])%MOD;
}
void cover(int i,int c)
{
cov[i]=c;fl[i]=0;
if(c==0) s[i]=0;
else s[i]=all[i];
}
void flip(int i)
{
s[i]=(all[i]-s[i]+MOD)%MOD;fl[i]^=1;
}
void down(int i)
{
if(cov[i]!=-1)
cover(i<<1,cov[i]),
cover(i<<1|1,cov[i]),cov[i]=-1;
if(fl[i])
flip(i<<1),flip(i<<1|1),fl[i]=0;
}
void work(int i,int l,int r,int L,int R,int f)
{
if(L>r || l>R) return ;
if(L<=l && r<=R)
{
if(f==1) flip(i);
if(f==2) cover(i,0);
if(f==3) cover(i,1);
return ;
}
int mid=(l+r)>>1;down(i);
work(i<<1,l,mid,L,R,f);
work(i<<1|1,mid+1,r,L,R,f);
s[i]=(s[i<<1]+s[i<<1|1])%MOD;
}
int find(int i,int l,int r,int L,int R)
{
if(L>r || l>R || !s[i]) return 0;
if(l==r) return l;
int mid=(l+r)>>1,t=0;down(i);
if(t=find(i<<1|1,mid+1,r,L,R)) return t;
return find(i<<1,l,mid,L,R);
}
int ask(int i,int l,int r,int L,int R)
{
if(L>r || l>R) return 0;
if(L<=l && r<=R) return s[i];
int mid=(l+r)>>1;down(i);
return ask(i<<1,l,mid,L,R)+
ask(i<<1|1,mid+1,r,L,R);
}
void add(int &x,int y) {x=(x+y)%MOD;}
int dt(int x) {return ((x+1)*pw[x]%MOD+1)%MOD;}
int ask(int l,int r)
{
int f=find(1,1,n,l,r),ans=0;
if(!f) return 0;
int g=find(1,1,n,l,f-1);f-=l;
if(!g) return (f+1)*(f+2)%MOD*inv2%MOD*pw[f]%MOD;
g-=l;
ans=(f+1)*(f+2)%MOD*inv2%MOD*pw[f]%MOD;
add(ans,dt(f+1));
add(ans,(2*f-g+3)*g%MOD*inv2%MOD*pw[f]);
add(ans,pw[g]-1);
add(ans,dt(f-g)*ask(1,1,n,l,g+l-1)%MOD*inv[l]);
return ans;
}
signed main()
{
freopen("run.in","r",stdin);
freopen("run.out","w",stdout);
n=read();m=read();pw[0]=inv[0]=1;
for(int i=1;i<=n;i++)
{
scanf("%1d",&a[i]);
pw[i]=pw[i-1]*2%MOD;
inv[i]=inv[i-1]*inv2%MOD;
}
build(1,1,n);
for(int i=1;i<=m;i++)
{
int op=read(),l=read(),r=read();
if(op<=3) work(1,1,n,l,r,op);
else printf("%lld\n",ask(l,r));
}
}
