[冲刺国赛2022] 模拟赛8
没有 \(\tt T2\),因为考试的时候就比较会,而且有点麻烦,不打算写了。
益智游戏
题目描述

\(n\leq 2000\)
解法
直接做并不容易,但是感觉本题应该有很好的性质,可以来分析一下。
首先忽略行之间的限制,只考虑单独一行的限制,发现有很好的分段结构,即 (22..2)-(11..1/33..3)-(44..4)
现在再把行之间的限制加上去,首先上下相邻的 \(1,3\) 不能 \(3\) 在上 \(1\) 在下;而 \(1\) 不能在 \(2,4\) 的下面;\(3\) 不能在 \(2,4\) 的上面;最后 \(2,4\) 也不能上下相邻;那么全局也会呈现一个很好的结构:
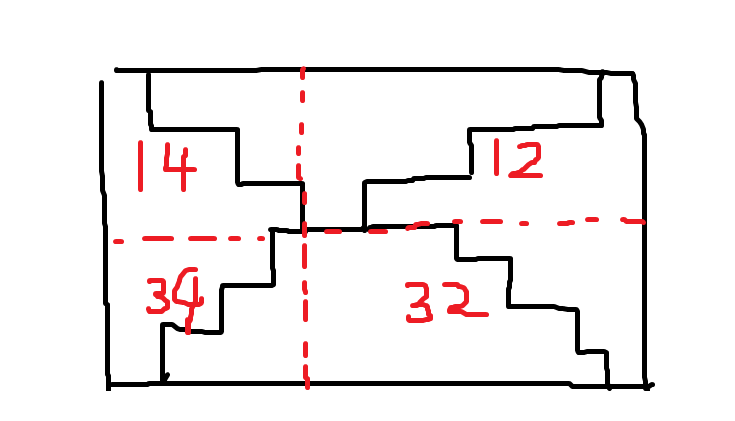
如图,全局分为上下两个部分,上面部分 \(1\) 的范围是越来越小的,下面部分 \(3\) 的范围是越来越大的。中间 \(1,3\) 的接壤处,必须要满足两个点的范围有交(特别地,如果有一方为空也视为有交),要不然会有 \(2,4\) 的限制。
拆解这个图的关键就是枚举这个交点,以交点划开整张图被分成了四部分。每一部分的最优解就是一个可以预处理 \(1,2,3,4\) 的前缀和,然后 \(dp\) 轮廓线。总时间复杂度 \(O(n^2)\)
#include <cstdio>
#include <iostream>
using namespace std;
const int M = 2005;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,ans,x[M][M],y[M][M];
int a[M][M],b[M][M],c[M][M],d[M][M];
int f1[M][M],f2[M][M],f3[M][M],f4[M][M];
signed main()
{
freopen("game.in","r",stdin);
freopen("game.out","w",stdout);
n=read();ans=1e18;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
x[i][j]=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
y[i][j]=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
a[i][j]=a[i-1][j];
if(x[i][j]!=1) a[i][j]+=y[i][j];
d[i][j]=d[i][j-1];
if(x[i][j]!=4) d[i][j]+=y[i][j];
}
for(int i=n;i>=1;i--)
for(int j=n;j>=1;j--)
{
c[i][j]=c[i+1][j];
if(x[i][j]!=3) c[i][j]+=y[i][j];
b[i][j]=b[i][j+1];
if(x[i][j]!=2) b[i][j]+=y[i][j];
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)//14
f1[i][j]=min(f1[i][j-1]+a[i][j],f1[i-1][j]+d[i][j]);
for(int i=1;i<=n;i++)
for(int j=n;j>=1;j--)//12
f2[i][j]=min(f2[i][j+1]+a[i][j],f2[i-1][j]+b[i][j]);
for(int i=n;i>=1;i--)
for(int j=1;j<=n;j++)//34
f3[i][j]=min(f3[i][j-1]+c[i][j],f3[i+1][j]+d[i][j]);
for(int i=n;i>=1;i--)
for(int j=n;j>=1;j--)//32
f4[i][j]=min(f4[i][j+1]+c[i][j],f4[i+1][j]+b[i][j]);
for(int i=0;i<=n;i++)
for(int j=0;j<=n;j++)
ans=min(ans,f1[i][j]+f2[i][j+1]+f3[i+1][j]+f4[i+1][j+1]);
printf("%lld\n",ans);
}
区间距离
题目描述
有两个长度为 \(n\) 的序列 \(a_1,a_2...a_n\) 和 \(b_1,b_2...b_n\)
\(m\) 次询问,每次给定 \(p_1,p_2,x\),询问下式的值:
\(n\leq 10^5,m\leq 10^6,1\leq a_i,b_i\leq 5\)
解法
突破本题的关键点肯定是值域,而这种绝对值的和式有一个很好的微元贡献法(我已经是第三次见到了,但不明白为什么我做这题没有任何优势,可能是没时间仔细想了)
我们枚举 \(k\in[1,4]\),把 \(\leq k\) 的数标记为 \(1\),把 \(>k\) 的数标记为 \(0\),那么在询问时,我们把对应位置的数异或起来,那么异或值就是对答案的贡献。
如果要暴力地优化这个暴力算法,可以考虑拆位。我们每 \(64\) 位压缩成一个 unsigned long long,预处理出以 \(0\sim 63\) 为起点的压位结果。这样计算的时候就可以暴力遍历,由于我们预处理了模 \(64\) 所有余数的压位结果,那么两边就是一定对应得上的。
时间复杂度 \(O(nw+\frac{nm}{w})\)
#pragma GCC target("popcnt")
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 100005;
const int N = 1000005;
#define ull unsigned long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
void write(int x)
{
if(x>=10) write(x/10);
putchar(x%10+'0');
}
int n,m,a[M],b[M],p[N],s[N],t[N],ans[N];
int f[M],g[M];ull F[64][2000],G[64][2000];
void solve()
{
for(int i=0;i<64;i++) for(int j=i;j<n;j+=64)
for(int k=0;k<64;k++)
{
F[i][j>>6]|=((ull)f[j+k])<<k;
G[i][j>>6]|=((ull)g[j+k])<<k;
}
for(int i=1;i<=m;i++)
{
ull *fp=F[s[i]&63]+(s[i]>>6);
ull *gp=G[t[i]&63]+(t[i]>>6);
int r=0,u=0;
for(;u+512<=p[i];u+=512,fp+=8,gp+=8)
{
#define g(x) __builtin_popcountll(x)
r+=g(fp[0]^gp[0]);
r+=g(fp[1]^gp[1]);
r+=g(fp[2]^gp[2]);
r+=g(fp[3]^gp[3]);
r+=g(fp[4]^gp[4]);
r+=g(fp[5]^gp[5]);
r+=g(fp[6]^gp[6]);
r+=g(fp[7]^gp[7]);
#undef g
}
for(;u<p[i];u++) r+=f[s[i]+u]^g[t[i]+u];
ans[i]+=r;
}
}
signed main()
{
freopen("dist.in","r",stdin);
freopen("dist.out","w",stdout);
n=read();m=read();
for(int i=0;i<n;i++) a[i]=read();
for(int i=0;i<n;i++) b[i]=read();
for(int i=1;i<=m;i++)
s[i]=read()-1,t[i]=read()-1,p[i]=read();
for(int w=1;w<=4;w++)
{
for(int i=0;i<n;i++)
f[i]=(a[i]<=w),g[i]=(b[i]<=w);
solve();
}
for(int i=1;i<=m;i++)
write(ans[i]),puts("");
}



