[做题笔记] zzz 的 string & dp 选讲
[POI2011] OKR-Periodicity
题目描述
解法
考虑递归地构造,设 solve(s) 表示字典序最小的,\(border\) 集合和 \(S\) 的 \(border\) 集合相等的字符串。
设 \(S\) 的最长 \(border\) 是 \(t\),我们分下列几种情况讨论:
第一种情况,\(S\) 不存在 \(border\),那么最优的方案就是 0,0...1(长度为 \(1\) 的话就是 0)
第二种情况,\(S\) 最长 \(border\) 小于 \(\lfloor\frac{n+1}{2}\rfloor\),那么 \(S\) 的其他 \(border\) 也是 \(S[1,2...t]\) 的 \(border\),所以我们递归地构造 \(S[1,2...t]\),然后考虑中间段怎么填,我们先尝试全填 \(0\),如果不行就把最后一个 \(0\) 改成 \(1\),可以证明这样构造一定是合法的。
合法的条件是不出现更长的 \(border\),假设中间段填成
0,0...0会出现更长的 \(border\),使用反证法,考虑中间段填成0,0...1也会出现更长的 \(border\)如果新 \(border\) 的长度 \(>\frac{n}{2}\),这样原串的周期至少循环了两次,考虑那个先填 \(0\) 再填 \(1\) 的位置,他一定和另一个固定的位置相对应,所以 \(0/1\) 中一定有一个会破坏周期,自然也就是不存在这样的 \(border\)
如果新 \(border\) 的长度 \(\leq \frac{n}{2}\),我们把新 \(border\) 的对应关系画出来:
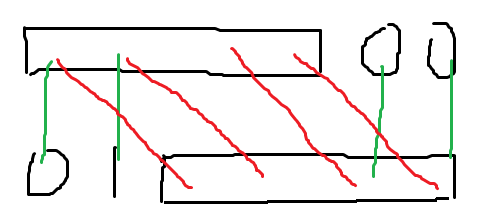
其中红线表示原来 \(border\) 的对应关系,绿线表示新 \(border\) 的对应关系。那么对于上面的最后一段 \(0\),新 \(border\) 对应到的下面的部分,一定含有一个 \(1\),导致无法匹配,所以不存在这样的 \(border\)
第三种情况,最短周期 \(\leq\lfloor\frac{n}{2}\rfloor\),我们递归地构造第一个循环 \(+\) 后面的零散部分即可。
简单地说明一下正确性,设最短周期 \(p=n-t\),设某一个周期是 \(q\),我们要满足所有的 \(q\),分类讨论:
如果 \(q\leq n-p\),根据弱周期引理,如果 \(p+q\leq n\),那么 \(\gcd (p,q)\) 也是一个周期。由于 \(p\) 是最短周期,那么 \(q\) 一定是 \(p\) 的倍数,我们发现根据构造方法,所以 \(p\) 的倍数的周期都是能被构造出来的。
如果 \(q>n-p\),那么对应的 \(border\) 小于等于 \(p\),我们把第一个循环和后面的零散部分拼起来,一定可以表示出这样的 \(border\)(本来 \(border\) 应该使用最后一个循环,平移到第一个循环是等效的)
由于最多递归 \(O(\log n)\) 次,时间复杂度 \(O(n\log n)\)
#include <cstdio>
#include <cassert>
#include <iostream>
using namespace std;
const int M = 200005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int T,nxt[M];string s;
int get(string x)
{
int n=x.length();
for(int i=2,j=0;i<=n;i++)
{
while(j && x[j]!=x[i-1]) j=nxt[j];
if(x[j]==x[i-1]) j++;
nxt[i]=j;
}
return nxt[n];
}
string solve(string x)
{
int t=get(x),n=x.length();
string y,r;r.resize(n);
if(t==0)
{
if(n==1) return "0";
for(int i=0;i+1<n;i++) r[i]='0';
r[n-1]='1';
return r;
}
if(t<(n+1)/2)
{
for(int i=0;i<t;i++) y+=x[i];
string h=solve(y);
for(int i=0;i<t;i++)
r[i]=r[n-t+i]=h[i];
for(int i=t;i<=n-t-1;i++)
r[i]='0';
if(get(r)!=t) r[n-t-1]='1';
}
else
{
t=n-t;
for(int i=0;i<t;i++) y+=x[i];
for(int i=n-(n%t);i<n;i++) y+=x[i];
string h=solve(y);
for(int i=0;i<n;i++) r[i]=h[i%t];
}
return r;
}
void work()
{
cin>>s;
cout<<solve(s)<<endl;
}
signed main()
{
T=read();
while(T--) work();
}
Fedya the Potter Strikes Back
题目描述
解法
由于本题要求强制在线,所以我们只能使用增量法,即在线地维护一个 \(border\) 集合,每次加入一个字符之后快速求出这些 \(border\) 对应的权值。
首先考虑加入字符 \(c_i\) 之后如何维护所有 \(border\),具体步骤是:
- 如果某个原有 \(border\) 的下一位字符不是 \(c\),把这个 \(border\) 删除;否则把这个位置保留。
- 如果 \(c_1=c_i\),那么新加入一个长度为 \(1\) 的 \(border\)
由于最多只会有 \(O(n)\) 个 \(border\) 会被加入,所以如果我们 \(O(1)\) 地找到需要被删除的 \(border\),那么可以在均摊 \(O(n)\) 的时间维护出 \(border\) 集合。
由于这些 \(border\) 都在最长 \(border\) 到 \(1\) 的链上,所以我们维护 \(fa_i\) 表示下一个字符与 \(c_{i+1}\) 不一样的,从 \([1,i]\) 跳 \(nxt\) 指针可以访问到的第一个 \(border\),那么我们在当前 \(border\) 不需要删除的时候,通过跳 \(fa\) 指针来找到需要删除的那个 \(border\)
维护出了 \(border\) 集合,现在考虑如何维护其对应的权值和。可以考虑用 map 存下每种权值的出现次数,加入一个权值的时候维护单调栈,把 \(>w_i\) 的权值删除,并全部转化成 \(w_i\) 即可。在删除 \(border\) 的时候可以在单调栈上二分以获取它的权值。
时间复杂度 \(O(n\log n)\)
#include <cstdio>
#include <vector>
#include <iostream>
#include <map>
using namespace std;
const int M = 600005;
#define int long long
#define hh __int128
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,now,h[M],w[M],nxt[M],fa[M],s[M];
hh ans;map<int,int> mp;
void write(hh x)
{
if(x>=10) write(x/10);
putchar(x%10+'0');
}
signed main()
{
n=read();
for(int i=1,j=0;i<=n;i++)
{
char c=getchar();w[i]=read();
s[i]=(c-'a'+ans)%26;
w[i]=(ans&((1<<30)-1))^w[i];
while(j && s[j+1]^s[i]) j=nxt[j];
if(i>1) j+=s[i]==s[j+1];
nxt[i]=j;
fa[i-1]=s[i]==s[nxt[i-1]+1]?
fa[nxt[i-1]]:nxt[i-1];
//
for(int k=i-1;k>=1;)
{
if(s[k+1]==s[i]) {k=fa[k];continue;}
int x=w[*lower_bound(h+1,h+1+m,i-k)];
mp[x]--;now-=x;
if(!mp[x]) mp.erase(x);
k=nxt[k];
}
while(m && w[h[m]]>=w[i]) m--;
int cnt=0;vector<int> d;
for(auto it=mp.upper_bound(w[i]);it!=mp.end();it++)
{
now+=(w[i]-it->first)*it->second;
cnt+=it->second;
d.push_back(it->first);
}
for(int x:d) mp.erase(x);
mp[w[i]]+=cnt;h[++m]=i;
if(i>1 && s[i]==s[1])
now+=w[i],++mp[w[i]];
ans+=now+w[h[1]];
write(ans);puts("");
}
}
[JSOI2019] 节日庆典
题目描述
给定一个长为 \(n\) 的字符串 \(S\),求它所有前缀的循环移位最小表示法的开头位置,相同的输出最靠前的一个。
\(n\leq 3\cdot 10^6\)
解法
使用增量法添加字符,可以维护一个备选后缀集合,只有这个集合中的后缀才可能成为最优解。类似斜率优化,如果后缀 \(a\) 之后永远不可能成为答案,那么就把后缀 \(a\) 删除。
集合中的元素最多只有 \(O(\log n)\) 个,证明如下:
考虑相邻的两个可能成为最优解的后缀 \(i,j\),如果 \(|j|<|i|<2|j|\),由于 \(j\) 是 \(i\) 的前缀(字典序暂时无法区分),那么 \(i\) 可以表示成 \(AAB\),\(j\) 可以表示成 \(AB\),存在一个后缀 \(k\) 可以表示成 \(B\)
如果 \(A=B\),\(j\) 不可能成为最优解,因为如果 \(A[1]>S[1]\),那么 \(k\) 比 \(j\) 优;如果 \(A[1]<S[1]\),那么 \(i\) 比 \(j\) 优;否则 \(A[1]=S[1]\),\(j\) 也不优于 \(i,k\)(这点有点难以解释,留给读者自证)
如果 \(B\) 是 \(A\) 的一个严格前缀,\(j\) 也不可能成为最优解,因为如果 \(A[|B|+1]>S[1]\),那么 \(k\) 比 \(j\) 优;如果 \(A[|B|+1]<S[1]\),那么 \(i\) 比 \(j\) 优;否则 \(A[|B|+1]=S[1]\),\(j\) 也不优于 \(i,k\)
可以按照证明的思路来维护这个集合,能直接区分是最好,如果区分不了可以用长度关系来判断,当小后缀的长度的两倍 \(>\) 大后缀的长度时,就可以弹出小后缀了。
在备选集合中求最优解可以考虑扩展 \(\tt kmp\),我们求出 \(nxt[i]\) 表示后缀 \(i\) 和原串的 \(\tt lcp\),这个问题就易于解决了,时间复杂度 \(O(n\log n)\)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <ctime>
using namespace std;
const int M = 3000005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,t1,t2,f[35],g[35],nx[M];char s[M];
void init()
{
for(int i=2,j=0,p=1;i<=n;i++)
{
j=max(min(nx[i-p+1],p+nx[p]-i),0);
while(i+j<=n && s[i+j]==s[j+1]) j++;
nx[i]=j;
if(p+nx[p]<i+nx[i]) p=i;
}
nx[1]=n;
}
int cmp(int x,int r)// compare [x...r] and [1...]
{
if(x+nx[x]-1>=r) return 0;
return s[nx[x]+1]<s[x+nx[x]]?1:-1;
}
int get(int x,int y,int r)// x>y compare [x..r] and [y..r]
{
int t=0;
if(t=cmp(y+r-x+1,r)) return t>0?x:y;
if(t=cmp(r-x+2,y-1)) return t>0?y:x;
return y;
}
signed main()
{
scanf("%s",s+1);n=strlen(s+1);
init();
for(int i=1;i<=n;i++)
{
swap(f,g);swap(t1,t2);f[t1=1]=i;
for(int j=1;j<=t2;j++) while(t1)
{
int x=g[j],y=f[t1];
//x is useless
if(s[x+(i-y)]>s[i]) break;
//can't distinguish them
if(s[x+(i-y)]==s[i])
{
//y is useless
if((i-y+1)*2>i-x+1) t1--;
f[++t1]=x;break;
}
//y is useless
t1--;if(!t1) {f[++t1]=x;break;}
}
int ans=f[1];
for(int j=2;j<=t1;j++)
ans=get(ans,f[j],i);
printf("%d ",ans);
}
}
[SDOI2017] 苹果树
题目描述
解法
抄的 Claris 的代码,题目很妙,代码好写,只是我指针熟练度为零。
考虑 \(t-h\leq k\) 的实际意义:我们可以选取一条到叶子的链免费获取(不是最长的一定不优),其他用树上依赖背包来付费获取,选取儿子的前提是选取父亲,背包大小为 \(k\)
考虑枚举我们选取的一条链,类似序列上的前后缀背包合并,我们求出正 \(\tt dfn\) 序的背包和逆 \(\tt dfn\) 序的背包,然后把它们合并起来就可以得到答案。
求解正序背包时,我们把必须选取的点(指选某个点导致其链上的点必须选取)和随意选取的点分开。进入一个点的时候加入随意选取的点,递归时把当前背包复制给儿子,然后从儿子回溯时加入当前点。
向背包中加入随意选取的点时,可以用单调队列优化,那么单次就是 \(O(k)\) 的。
求解逆序背包时,我们把每个点的连边顺序反过来,然后同样地递归,此时和正序背包的唯一区别就是在当前点回溯的时候加入随意选取的点。
设求出来的正序背包和逆序背包分别是 \(f[u][i]\) 和 \(h[u][i]\),那么合并答案时就用 \(f[u][i]+h[u][k-i]+\)当前链的长度即可,时间复杂度 \(O(nk)\),为了节省空间,\(dp\) 过程需要用指针实现。
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
using namespace std;
const int M = 500005;
const int N = 26000005;
#define pb push_back
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int T,n,m,k,ans,fa[M],a[M],b[M],f[N],h[N];
vector<int> g[M];
void solve(int *f,int A,int B)
{
static int p[M]={},q[M]={};
int h=1,t=0;
for(int i=0,j=0;i<=m;i++,j+=B)
{
while(h<=t && p[t]<=f[i]-j) t--;
p[++t]=f[i]-j;q[t]=i;
while(h<=t && q[h]<i-A) h++;
f[i]=p[h]+j;
}
}
void dfs1(int u)
{
if(a[u]) solve(f+u*k,a[u],b[u]);
for(int v:g[u])
{
memcpy(f+v*k,f+u*k,T);
dfs1(v);
int *s=f+u*k+1,*e=f+v*k;
for(int i=1;i<=m;i++,s++,e++)
*s=max(*s,*e+b[v]);
}
}
void dfs2(int u,int x)
{
x+=b[u];
for(int v:g[u])
{
memcpy(h+v*k,h+u*k,T);
dfs2(v,x);
int *s=h+u*k+1,*e=h+v*k;
for(int i=1;i<=m;i++,s++,e++)
*s=max(*s,*e+b[v]);
}
if(g[u].empty())
{
int *s=f+u*k+m,*e=h+u*k;
for(int i=0;i<=m;i++,s--,e++)
ans=max(ans,*s+*e+x);
}
if(a[u]) solve(h+u*k,a[u],b[u]);
}
void work()
{
n=read();m=read();ans=0;
k=m+1;T=k*sizeof(int);
memset(f,0,sizeof f);
memset(h,0,sizeof h);
for(int i=1;i<=n;i++) g[i].clear();
for(int i=1;i<=n;i++)
{
fa[i]=read();
if(i>1) g[fa[i]].pb(i);
a[i]=read()-1;b[i]=read();
}
dfs1(1);
for(int i=1;i<=n;i++) g[i].clear();
for(int i=n;i>1;i--) g[fa[i]].pb(i);
dfs2(1,0);
printf("%d\n",ans);
}
signed main()
{
int Case=read();
while(Case--) work();
}
[HDU6566] The Hanged Man
题目描述
求一个树上的独立集,使得点权 \(a_i\) 求和为 \(x\),并使得点权 \(b_i\) 求和最大。
需要对于每个 \(x\in[1,m]\) 都求出满足条件的独立集数量。
\(n\leq 50,a_i\leq m\leq 5000,b_i\leq 10^6\)
解法
单次背包至少需要 \(O(m^2)\),是行不通的。
考虑以某种顺序依次加入点,但是这样需要记录已加入点的状态,如果暴力来做的话是 \(O(2^n\cdot nm)\) 的。
考虑优化这个加入顺序,对于一个点,我们先加入其重儿子,然后加入这个点,最后加入它的轻儿子。发现访问到一个点时,我们只需要记录它走了轻边的祖先的状态(走了重边的祖先还未加入),所以状态数是 \(O(nm)\) 的。
具体实现中,我们在从重儿子回溯时,把记录重儿子的状态抛弃掉,再加入当前点的状态,时间复杂度 \(O(n^2m)\)
#include <cstdio>
#include <vector>
#include <iostream>
using namespace std;
const int M = 55;
const int N = 5005;
const int Log = 7;
const int inf = 0x3f3f3f3f;
#define ll long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int T,n,m,k,a[M],b[M],id[M];
int siz[M],son[M];vector<int> g[M];
struct node
{
int x;ll y;
node(int X=-inf,ll Y=0) : x(X) , y(Y) {}
void clear() {x=-inf;y=0;}
node operator + (const int &b) const
{return node(x+b,y);}
node operator & (const node &b) const
{
node r=b;
if(r.x<x) r.x=x,r.y=0;
if(r.x==x) r.y+=y;
return r;
}
}dp[1<<Log][N],t[1<<Log][N];
void pre(int u,int fa)
{
siz[u]=1;son[u]=0;
for(int v:g[u]) if(v^fa)
{
pre(v,u);siz[u]+=siz[v];
if(siz[son[u]]<siz[v]) son[u]=v;
}
}
void recycle(int p)
{
k--;
for(int x=0;x<(1<<k-p);x++)
for(int y=0;y<(1<<p);y++) for(int i=0;i<=m;i++)
t[(x<<p)|y][i]=dp[(x<<p+1)|(1<<p)|y][i]
&dp[(x<<p+1)|y][i];
for(int s=0;s<(1<<k);s++)
for(int i=0;i<=m;i++)
dp[s][i]=t[s][i],t[s][i].clear();
}
void dfs(int u,int fa)
{
id[u]=Log;
if(son[u]) dfs(son[u],u);
id[u]=k++;
for(int S=0;S<(1<<id[u]);S++)
{
int T=S|(1<<id[u]);
for(int i=0;i<a[u];i++) dp[T][i].clear();
if((T>>id[fa]&1) || (T>>id[son[u]]&1))
for(int i=a[u];i<=m;i++)
dp[T][i].clear();
else for(int i=a[u];i<=m;i++)
dp[T][i]=dp[S][i-a[u]]+b[u];
}
if(son[u]) recycle(id[u]=id[son[u]]);
for(int v:g[u]) if(v^fa && v^son[u])
dfs(v,u),recycle(id[v]);
}
void work()
{
n=read();m=read();k=0;id[0]=Log;
for(int i=1;i<=n;i++)
a[i]=read(),b[i]=read(),g[i].clear();
for(int i=1;i<n;i++)
{
int u=read(),v=read();
g[u].push_back(v);
g[v].push_back(u);
}
dp[0][0]=node(0,1);
for(int i=1;i<=m;i++) dp[0][i].clear();
pre(1,0);dfs(1,0);
recycle(id[1]);
for(int i=1;i<=m;i++)
{
printf("%lld",dp[0][i].y);
if(i<m) putchar(' ');
}
puts("");
}
signed main()
{
T=read();
for(int i=1;i<=T;i++)
{
printf("Case %d:\n",i);
work();
}
}
Foreigner
题目描述
解法
可以用刷表法来构造所有合法的数字,写成代码是这样的:
for(int i=1;i<=9;i++) q[++t]=i;
while(1)
{
int u=q[h++];
for(int i=0;i<h%11;i++)
q[++t]=q[h]*10+i;
}
考虑计算往数列中第 \(i\) 个数后面接一个 \(c\),得到的数字的排名是多少,由于这个数列是根据生成顺序递增的,所以我们只需要计算比它小的数的个数:
由于我们只需要判断一个数字是不是合法数字,可以把排名计算式都放在 \(\bmod 11\) 的意义下:
那么对于原来的计数问题,可以考虑设计一个自动机来转移,自动机上每个元素是。设 \(dp[i][j]\) 表示考虑前 \(i\) 个字符,现在有多少个以 \(i\) 结尾的子串处于自动机上第 \(j\) 个节点。
使用整体 \(dp\) 的技巧,我们在左端点初始化,走到右端点时在自动机上拿答案,时间复杂度 \(O(n)\)
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int M = 100005;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,ans,f[M][15];char s[M];
int nxt(int x,int c)
{
return (x*(x-1)/2+c+10)%11;
}
signed main()
{
scanf("%s",s+1);n=strlen(s+1);
for(int i=1;i<=n;i++)
{
int c=s[i]-'0';
for(int j=c+1;j<=10;j++)
f[i][nxt(j,c)]+=f[i-1][j];
if(c) f[i][c]++;
for(int j=0;j<=10;j++) ans+=f[i][j];
}
printf("%lld\n",ans);
}




