[冲刺国赛2022] 模拟赛7
小学生物理题
题目描述
给定 \(n+2\) 个节点在数轴上排成一排,编号 \(0,1...n+1\),节点 \(0\) 在 \(-\infty\) 的位置,节点 \(1\) 在原点,对于 \(i=1,2...n-1\),节点 \(i+1\) 在节点 \(i\) 正方向距离 \(s_i\) 的位置,节点 \(n+1\) 在 \(+\infty\) 的位置。
对于 \(i=0,1...n\),节点 \(i\) 与节点 \(i+1\) 之间有一 条编号为 \(i\) 的导线。已知恰有一条导线断掉了,你需要找到这条导线并将其修复。你当前在原点,可以在数轴上任意移动,移动 \(x\) 单位长度的代价是 \(x\),若你当前在某个节点 ,则可以花费 \(d_i\) 的代价检查其与节点 \(0\) 是否连通。修复导线的代价是 \(F_i\)
求在所有策略中,所需代价之和的最大值(即最坏情况)的最小值是多少?
\(n\leq 3000\)
解法
本题的代价计算特别复杂,贪心是行不通的,直接考虑 \(dp\),设 \(f_{l,r,0/1}\) 表示还剩区间 \([l,r]\),现在人处在 \(l/r\),最坏情况的最小值是多少。转移枚举第一个检测的位置,如果检测结果是断开,那么说明断掉的导线在前面;如果检测结果是连通,那么说明断掉的导线在后面,最坏情况需要在两者中取最大值:
其中 \(s_i\) 表示 \(1\) 到 \(i\) 的距离,初始化 \(f_{i-1,i,0/1}=F_{i-1}\),最后的答案是 \(f_{0,n+1,0}\),暴力转移时间复杂度 \(O(n^3)\)
下文就针对第一个转移讲解,第二个转移的优化方法本质相同。
观察发现,转移式中的代价只和 \(k\) 有关,并且只要把 \(\max\) 拆开 \(l,r\) 就是独立的。那么如何把 \(\max\) 拆开呢?我们固定 \(r\) 移动 \(l\),由于 \(f_{l,r,0/1}\) 的单调性(\(l\) 减少,值增大;\(r\) 增加,值增大),所以一定存在一个分界点 \(p\),使得 \(f_{p,r,0}\geq f_{l,p,1}\),并且在 \(l\) 减小的过程中,\(p\) 也只会减小,所以可以双指针维护这个 \(p\)
对于 \(k\leq p\),代价是 \(f_{k,r,0}+s_k+d_k\),可以直接拿个单调队列来维护,在 \(p\) 减小的过程中弹出 \(k>p\) 的点即可。
对于 \(k>p\),代价是 \(f_{l,k,1}+s_k+d_k\),因为在 \(r\) 增大的过程中 \(p_l\) 是只会增大的(\(p_l\) 指的是 \(l\) 对应的 \(p\)),所以对于每个 \(l\) 都维护一个单调队列,在 \(p_l\) 增大的过程中弹出 \(k\leq p_l\) 的点即可。
时间复杂度 \(O(n^2)\)
#include <cstdio>
#include <iostream>
using namespace std;
const int M = 3005;
#define int long long
const int inf = 1e18;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,s[M],d[M],f[M],dp[M][M][2];
struct n1
{
int h,t,a[M],b[M];
void clear() {h=1;t=0;}
void ins(int p,int v)
{
while(h<=t && b[t]>=v) t--;
a[++t]=p;b[t]=v;
}
int get(int p)
{
while(h<=t && a[h]<p) h++;
return h<=t?b[h]:inf;
}
}A[M],B[M];
struct n2
{
int h,t,a[M],b[M];
void clear() {h=1;t=0;}
void ins(int p,int v)
{
while(h<=t && b[t]>=v) t--;
a[++t]=p;b[t]=v;
}
int get(int p)
{
while(h<=t && a[h]>p) h++;
return h<=t?b[h]:inf;
}
}C,D;
void upd(int l,int r)
{
A[l].ins(r,dp[l][r][1]+d[r]+s[r]);
B[l].ins(r,dp[l][r][1]+d[r]-s[r]);
C.ins(l,dp[l][r][0]+d[l]+s[l]);
D.ins(l,dp[l][r][0]+d[l]-s[l]);
}
signed main()
{
freopen("physics.in","r",stdin);
freopen("physics.out","w",stdout);
n=read();
for(int i=2;i<=n;i++) s[i]=s[i-1]+read();
for(int i=1;i<=n;i++) d[i]=read();
for(int i=0;i<=n;i++) f[i]=read();
for(int r=1;r<=n+1;r++)
{
int p=r-1;
dp[r-1][r][0]=dp[r-1][r][1]=f[r-1];
C.clear();D.clear();upd(r-1,r);
for(int l=r-2;l>=0;l--)
{
while(p>l && dp[l][p][1]>dp[p][r][0]) p--;
dp[l][r][0]=min(A[l].get(p+1),C.get(p))-s[l];
dp[l][r][1]=min(B[l].get(p+1),D.get(p))+s[r];
upd(l,r);
}
}
printf("%lld\n",dp[0][n+1][0]);
}
数轴变换
题目描述
\(\tt DD(XYX)\) 有一个空白的数轴,一开始 \(\tt DD(XYX)\) 把原点涂成黑色,现在有 \(q\) 次操作,你需要支持下面五种操作:
- 给定 \(x\),将整点 \(x\) 染成黑色。
- 给定 \(x\),对于整点 \(y\),如果存在整点 \(z\) 是黑色的且满足 \(|y-z|\leq x\),则将其染黑。
- 给定 \(l,r\),翻转区间 \([l,r]\),即对于所有的整点 \(x\in[l,r]\),将它的颜色设置为整点 \(r+l-x\) 的颜色。
- 给定 \(x\),将每个整点的颜色重设为第 \(x\) 次操作之后时的颜色,若 \(x=0\),则还原到初始状态(只有原点是黑色)
- 给定 \(x\),询问 \(x\) 是否是黑色的。
\(q\leq 2\cdot 10^5\),\(|l|,|r|,|x|\leq 10^{12}\),强制在线。
解法
看到强制在线,大概知道第 \(4\) 种操作就是给我们维护的数据结构套上可持久化,这个可以先扔一边。
只考虑操作 \(1,2\),原来操作 \(1\) 的单点经过操作 \(2\) 的影响之后会发散成区间,所以可以转化成更易于维护的差分标记。我们分别维护加法标记和减法标记,那么操作 \(1\) 就是在 \(x\) 处插入一个加法标记和一个减法标记,操作 \(2\) 就是把所有加法标记左移 \(x\),把所有减法标记右移 \(x\);查询时可以找到 \([1,x]\) 中的加法标记总个数,减去 \([1,x)\) 中的减法标记总个数,就可以判断这个点是否被覆盖。
考虑操作 \(3\),先考虑对于单个区间如何翻转:
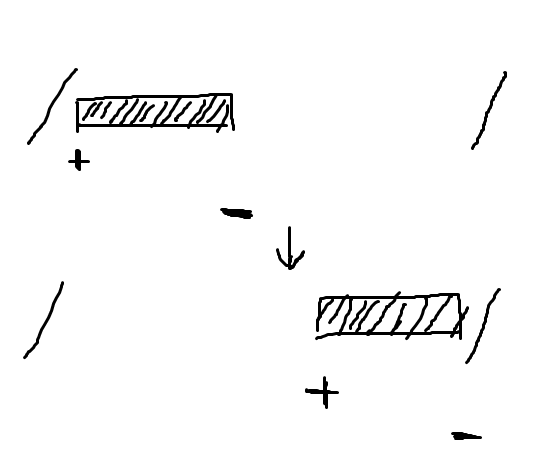
发现翻转规则是:加法标记和减法标记分别翻转,翻转之后交换所有加法标记和减法标记。当然这么做也是有一定条件的:也就是两个匹配的加法标记和减法标记构成的区间必须完全包含在翻转区间内。
现在操作 \(3\) 的难点是我们无法保证这样的翻转条件,考虑在不改变问题结构的情况下创造出这个条件。我们统计 \([1,l)\) 中加法标记与减法标记的差 \(x\),然后在 \(l-1\) 处添加 \(x\) 个减法标记,在 \(l\) 处添加 \(x\) 个加法标记。统计 \([1,r]\) 中加法标记与减法标记的差 \(x\),在 \(r\) 处添加 \(x\) 个减法标记,在 \(r+1\) 处添加 \(x\) 个加法标记。
容易发现这样处理,对于任意位置加法标记减去减法标记的数量是不改变的,并且区间 \([l,r]\) 已经被独立出来了(内部的加法标记和减法标记都可以自己匹配),可以直接按照上述规则翻转。具体实现中采用非旋 \(\tt treap\),可以打乘法标记和加法标记来支持翻转(这样也可以支持操作 \(2\) 的平移)
那么上一个可持久化非旋 \(\tt treap\) 即可,我们只需要在 \(\tt split/merge\) 以及修改权值的时候可持久化即可。\(\tt DD(XYX)\) 发现了一个关键的卡空间方法:记录某个点建立时的时间戳 \(tim\),如果 \(tim\) 等于现在操作的时间戳 \(T\),就可以不新建节点,因为这样并不会影响到之前的版本。
还有一个玄学问题是,加法标记和减法标记的数量可能达到指数级,所以需要自然溢出记录个数。时间复杂度 \(O(n\log n)\),空间需要抵着 \(1G\) 开,可以参考一下我的代码实现:
#include <cstdio>
#include <cassert>
#include <iostream>
#include <random>
using namespace std;
const int M = 200005;
#define ll long long
const int MD = (1<<30)-1;
ll read()
{
ll x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,NT,rt1[M],rt2[M];mt19937 g(114514);
struct node
{
int ls,rs,hp,vl,a;
unsigned int sm,tm;ll b,x;
node() {ls=rs=hp=vl=sm=b=x=0;a=1;}
}t[M*110];
void up(int x)
{
if(!x) return ;
int ls=t[x].ls,rs=t[x].rs;
t[x].sm=t[x].vl+t[ls].sm+t[rs].sm;
}
int get(int x)
{
if(!x || t[x].tm>=NT) return x;
int y=++n;t[y]=t[x];t[y].tm=NT;return y;
}
void upd(int x,int a,ll b)
{
if(!x) return ;
t[x].x=t[x].x*a+b;
t[x].a*=a;t[x].b=t[x].b*a+b;
if(a<0) swap(t[x].ls,t[x].rs);
}
void down(int x)
{
if(!x) return ;
int &ls=t[x].ls,&rs=t[x].rs;
ls=get(ls);rs=get(rs);
upd(ls,t[x].a,t[x].b);
upd(rs,t[x].a,t[x].b);
t[x].a=1;t[x].b=0;
}
void split(int x,ll y,int &a,int &b)
{
if(!x) {a=b=0;return ;}
down(x);
if(t[x].x<=y)
{
split(t[x].rs,y,t[x].rs,b);
a=x;up(x);return ;
}
split(t[x].ls,y,a,t[x].ls);
b=x;up(x);return ;
}
int merge(int x,int y)
{
if(!x || !y) return x+y;
if(t[x].hp<=t[y].hp)
{
down(x);
t[x].rs=merge(t[x].rs,y);
up(x);return x;
}
down(y);
t[y].ls=merge(x,t[y].ls);
up(y);return y;
}
int ins(int x,ll y,ll w)
{
int a=0,b=0,c=0,d=0;
split(get(x),y-1,a,b);split(get(b),y,c,d);
if(c) t[c].vl+=w,t[c].sm+=w;
else
{
c=++n;t[c].x=y;t[c].hp=g()&MD;
t[c].vl=t[c].sm=w;t[c].tm=NT;
}
return merge(get(a),merge(get(c),get(d)));
}
signed main()
{
freopen("trans.in","r",stdin);
freopen("trans.out","w",stdout);
m=read();
rt1[0]=ins(rt1[0],0,1);
rt2[0]=ins(rt2[0],0,1);
for(int i=1,ls=0;i<=m;i++)
{
rt1[i]=rt1[i-1];rt2[i]=rt2[i-1];
int op=read();NT++;
if(op==1)
{
ll x=read()^ls;
rt1[i]=ins(rt1[i],x,1);
rt2[i]=ins(rt2[i],x,1);
}
if(op==2)
{
ll x=read()^ls;
upd(rt1[i]=get(rt1[i]),1,-x);
upd(rt2[i]=get(rt2[i]),1,x);
}
if(op==3)
{
ll l=read()^ls,r=read()^ls;
int a=0,b=0,c=0,d=0,e=0,f=0;
split(get(rt1[i]),l-1,a,b);split(get(b),r,b,c);
split(get(rt2[i]),l-1,d,e);split(get(e),r,e,f);
ll x=t[a].sm-t[d].sm,y=t[f].sm-t[c].sm;
b=ins(b,l,x);d=ins(d,l-1,x);
c=ins(c,r+1,y);e=ins(e,r,y);
upd(b=get(b),-1,l+r);
upd(e=get(e),-1,l+r);
rt1[i]=merge(get(a),merge(get(e),get(c)));
rt2[i]=merge(get(d),merge(get(b),get(f)));
}
if(op==4)
{
ll x=read()^ls;
rt1[i]=rt1[x];rt2[i]=rt2[x];
}
if(op==5)
{
ll x=read()^ls;
int a=0,b=0,c=0,d=0;
split(get(rt1[i]),x,a,b);
split(get(rt2[i]),x-1,c,d);
unsigned int z=t[a].sm-t[c].sm;
assert(z>=0);
puts(z>0?"Yes":"No");ls+=(z>0);
rt1[i]=merge(get(a),get(b));
rt2[i]=merge(get(c),get(d));
}
}
}
中学生物理题
题目描述
在平面上放置 \(n\) 块双面镜子,它们与坐标轴成 \(45\) 度角摆放。它们的摆放方式可以由坐标 \((x_i,y_i)\) 和字符 / 或 \
从沿坐标轴平行的方向射出一束激光,激光经过镜子会顺\(/\)逆时针旋转 \(90\) 度,最终可能会陷入循环或无限地向某个方向射出。
你需要放 \(4\) 种类型的镜子,要求对于每个可能的循环,一次循环内经过每种类型镜子的次数相同且都为偶数。请构造一种方案,或者输出 -1 说明不存在合法方案。
\(n\leq 5\cdot 10^5\)
解法
首先考虑如何找出所有循环,我们先把一个镜子拆成两个点:
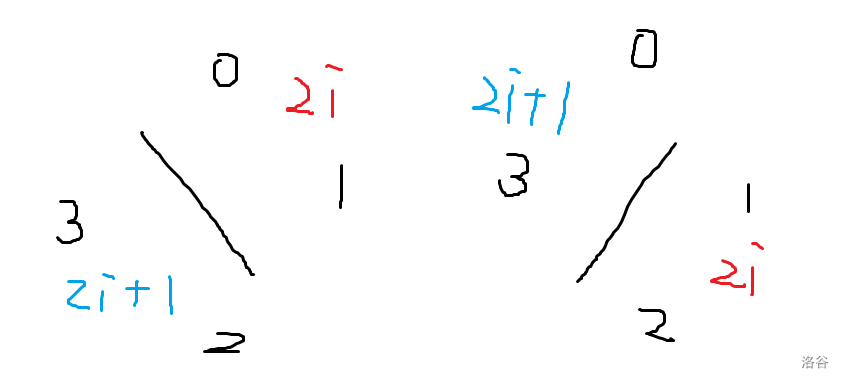
然后我们通过离散化,对于每一面镜子找到其四个方向的第一面镜子。特别地,如果某个方向没有镜子则找到代表无穷远处的虚空点。把对应点连边,那么循环一定是不含虚空点的一个连通块。
由于循环之间可能存在共用边的情况,这使得我们并不能独立染色。所以我们把循环当成点,把镜子当成边来处理这个限制。具体来说,拿到一面镜子拆成的两个点所属的循环,把这两个循环连边即可。特别地,如果某一边包含虚空点,这么连可以考虑到单独染色的贡献;如果连成的是自环,代表该颜色的染色会贡献两次。
不难发现有解的必要条件是:每个循环的度数都是 \(8\) 的倍数。下面通过构造法说明这也是一个充分条件:
我们首先把每个点连出去的边分成两组,要求每一组边的数量相等。可以通过欧拉回路来构造分组,也就是对于欧拉回路跑出来的环,我们 \(0,1,0,1...\) 地交替染色就可以完成分组。由于存在欧拉回路的充要条件是度数都是偶数,所以一定可以完成分组。
然后对于分成的两组,我们对每一组分别进行上述的分组操作。这样最后就得到了四组边,每组边的颜色是相同的,就成功构造出了答案,时间复杂度 \(O(n\log n)\)
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 1000005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,t,tot=1,f[M],cur[M];
int ans[M],fa[M],vis[M],d[M];
struct edge{int v,next;}e[M];
struct node
{
int x,y,c,p[4],id;
bool operator < (const node &b) const
{return x==b.x?y<b.y:x<b.x;}
}s[M];
int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
int get(int x,int d)
{
if(s[x].c==0)// "\"
return (x<<1)|(d==2||d==3);
return (x<<1)|(d==0||d==3);// "\"
}
void init()
{
sort(s+1,s+1+n);
static int b[M]={},h[M]={};
for(int i=1;i<=n;i++) b[i]=s[i].y;
sort(b+1,b+1+n);
int k=unique(b+1,b+1+n)-b-1;
for(int i=1;i<=n;i++)
s[i].y=lower_bound(b+1,b+1+k,s[i].y)-b;
for(int i=1,ls=0;i<=n;i++)
{
if(s[i].x!=s[i-1].x) ls=0;
s[i].p[3]=ls;//left
if(ls) s[ls].p[1]=i;//right
int t=h[s[i].y];
s[i].p[2]=t;//down
if(t) s[t].p[0]=i;//up
h[s[i].y]=ls=i;
}
}
void build()
{
m=n<<1|1;
for(int i=1;i<=m;i++) fa[i]=i;
for(int i=1;i<=n;i++) for(int d=0;d<4;d++)
{
int x=get(i,d),y=get(s[i].p[d],d^2);
x=find(x);y=find(y);if(x>y) swap(x,y);
fa[y]=x;//guarantee that 0 is father
}
for(int i=1;i<=n;i++)
{
int x=find(i<<1),y=find(i<<1|1);
e[++tot]=edge{x,f[y]},f[y]=tot;
e[++tot]=edge{y,f[x]},f[x]=tot;
d[x]++;d[y]++;
}
}
void dfs(int u)
{
for(int &i=cur[u];i;i=e[i].next)
if(vis[i>>1]==0)
{
int x=i>>1;vis[x]=-1;
dfs(e[i].v);
vis[x]=t;t^=1;
}
}
signed main()
{
freopen("scisyhp.in","r",stdin);
freopen("scisyhp.out","w",stdout);
n=read();
for(int i=1;i<=n;i++)
{
s[i].x=read();s[i].y=read();
s[i].c=getchar()=='/'?1:0;s[i].id=i;
}
init();build();
for(int i=1;i<=m;i++)
if(i==fa[i] && (d[i]&7))
{puts("-1");return 0;}
t=2;
for(int i=0;i<=m;i++) cur[i]=f[i];
for(int i=0;i<=m;i++) dfs(i);
//I
for(int i=1;i<=n;i++) if(vis[i]==2) vis[i]=0;
for(int i=0;i<=m;i++) cur[i]=f[i];
t=4;
for(int i=0;i<=m;i++) dfs(i);
//II
for(int i=1;i<=n;i++) if(vis[i]==3) vis[i]=0;
for(int i=0;i<=m;i++) cur[i]=f[i];
t=6;
for(int i=0;i<=m;i++) dfs(i);
//
for(int i=1;i<=n;i++)
ans[s[i].id]=vis[i]-3;
for(int i=1;i<=n;i++)
printf("%d ",ans[i]);
puts("");
}



